Eri muoto

Termi differentiaalimuoto (kutsutaan usein myös vaihtelevaksi differentiaalimuodoksi ) juontaa juurensa matemaatikko Élie Joseph Cartanille . Ero muodot ovat keskeinen käsite ero geometria . Ne mahdollistavat koordinaatista riippumattoman integroinnin yleisesti suuntautuviin erilaistuviin jakotukkiin .

yhteydessä

Olkoon se ${\ displaystyle U}$

• avoin osajoukko${\ displaystyle \ mathbb {R} ^ {n}}$
• tai erottuva alaryhmä${\ displaystyle \ mathbb {R} ^ {n}}$
• tai erilaistuva jakoputki .

Jokaisessa näistä tapauksista on

• käsite differentiable toiminnon tilaa äärettömän differentiable toimintoja menossa nimetty;${\ displaystyle U;}$${\ displaystyle U}$${\ displaystyle C ^ {\ infty} (U)}$
• käsite tangenttitilan pisteessä${\ displaystyle \ mathrm {T} _ {p} U}$${\ displaystyle U}$${\ displaystyle p \ U-muodossa;}$
• käsite suuntaa johdannaisen varten tangentiaalisen vektorin ja differentioituva funktio${\ displaystyle {\ tfrac {\ partis f} {\ osaa X}}}$${\ displaystyle X \ sisään \ mathrm {T} _ {p} U}$${\ displaystyle f;}$
• käsite differentioituva vektorin kenttä on tilaa vektorin kentät on merkitty.${\ displaystyle U;}$${\ displaystyle U}$${\ displaystyle \ Gamma (\ mathrm {T} U)}$

Duaaliavaruus on tangenttitilan kutsutaan kotangentin tilaa . ${\ displaystyle \ mathrm {T} _ {p} U}$ ${\ displaystyle \ mathrm {T} _ {p} ^ {*} U}$

määritelmä

Eri muoto

Ero muodossa aste on${\ displaystyle k}$${\ displaystyle U}$ tai lyhyt muoto on sileä leikkaus on th ulompi teho on Kotangentialbündels on . Symbolisessa notaatiotamme avulla , jolloin kotangentti nippu , th ulompi voima ja siten määrää sileän osien nimetty. ${\ displaystyle k}$ ${\ displaystyle \ omega}$${\ displaystyle k}$${\ displaystyle U}$${\ displaystyle \ omega \ Gammassa (\ Lambda ^ {k} (T ^ {*} U))}$${\ displaystyle T ^ {*} U}$${\ displaystyle U}$${\ displaystyle \ Lambda ^ {k} (T ^ {*} U)}$${\ displaystyle k}$${\ displaystyle T ^ {*} U}$${\ displaystyle \ Gamma (\ Lambda ^ {k} (T ^ {*} U))}$${\ displaystyle \ Lambda ^ {k} (T ^ {*} U)}$

Tämä tarkoittaa, että tangenttitilassa on vuorotellen monirivinen muoto kullekin pisteelle ; siten, että tasaisille vektorikentille funktio ${\ displaystyle p \ in U}$ ${\ displaystyle \ omega _ {p}}$${\ displaystyle T_ {p} U}$${\ displaystyle k}$${\ displaystyle X_ {1}, \ ldots, X_ {k}}$

${\ displaystyle p \ mapsto \ omega _ {p} ((X_ {1}) _ {p}, \ ldots, (X_ {k}) _ {p}) \ in \ mathbb {R}}$

on sileä , ts. erotettavissa niin usein kuin halutaan.

Vaihtoehtoisesti -muoto voidaan nähdä vaihtoehtoisena, sileä usean muuttujan kartoitus . Tämä tarkoittaa: määrittää funktion vektorikentille niin ${\ displaystyle k}$${\ displaystyle \ omega}$${\ displaystyle \ omega \ kaksoispiste (\ Gamma TU) ^ {k} \ - C ^ {\ infty} (U)}$${\ displaystyle \ omega}$${\ displaystyle k}$ ${\ displaystyle X_ {1}, \ ldots, X_ {k}}$${\ displaystyle \ omega (X_ {1}, \ ldots, X_ {k})}$

• ${\ displaystyle \ omega (X_ {1}, \ ldots, X '_ {i} + X' '_ {i}, \ ldots, X_ {k}) = \ omega (X_ {1}, \ ldots, X '_ {i}, \ ldots, X_ {k}) + \ omega (X_ {1}, \ ldots, X' '_ {i}, \ ldots, X_ {k})}$
• ${\ displaystyle \ omega (X_ {1}, \ ldots, f \ cdot X_ {i}, \ ldots, X_ {k}) = f \ cdot \ omega (X_ {1}, \ ldots, X_ {i}, \ ldots, X_ {k})}$ Sillä ${\ displaystyle f \ muodossa C ^ {\ infty} (U), 1 \ leq i \ leq k}$

ja

• ${\ displaystyle \ omega (X_ {1}, \ ldots, X_ {i}, \ ldots, X_ {j}, \ ldots, X_ {k}) = - \ omega (X_ {1}, \ ldots, X_ { j}, \ ldots, X_ {i}, \ ldots, X_ {k})}$

sovelletaan.

Vaihtoehto tensorikenttien käyttämiseen : Lomake on tason vuorotteleva, kovariittinen tensorikenttä${\ displaystyle k}$${\ displaystyle k.}$

Eri muotojen tila

Joukko muotoja muodostaa vektori tilaa ja on merkitty. Jatat vetoa ${\ displaystyle k}$${\ displaystyle U}$${\ displaystyle \ Omega ^ {k} (U)}$

${\ displaystyle \ Omega (U) = \ bigoplus _ {k = 1} ^ {\ infty} \ Omega ^ {k} (U).}$

Äärellinen-ulotteinen manifolds tämä summa on äärellinen, koska vektori tila on nolla vektori tilaa . Joukko on algebra , jonka ulkotulo on kertolasku ja siten jälleen vektoritila. Vuodesta topologinen näkökulmasta tämä tila on myös nippu . ${\ displaystyle k> \ himmeä U}$${\ displaystyle \ Omega ^ {k} (U)}$${\ displaystyle \ Omega (U)}$

Voidaan ymmärtää se ulkoisen voiman elementtinä ; siten ulompi tuote (ts . ulomman algebran tuote ) määrittelee kartat ${\ displaystyle \ omega _ {p}}$ ${\ displaystyle \ Lambda ^ {k} (T_ {p} ^ {*} U)}$${\ displaystyle \ wedge}$

${\ displaystyle \ Omega ^ {k} (U) \ times \ Omega ^ {\ ell} (U) \ to \ Omega ^ {k + \ ell} (U), \ quad (\ omega, \ eta) \ mapsto \ omega \ wedge \ eta,}$

on kautta ${\ displaystyle \ omega \ wedge \ eta}$

${\ displaystyle (\ omega \ wedge \ eta) _ {p} = \ omega _ {p} \ wedge \ eta _ {p}}$

on määritelty pisteittäin.

Tämä tuote on porrastettu-kommutatiivinen , sitä sovelletaan

${\ displaystyle \ omega \ wedge \ eta = (- 1) ^ {\ deg \ omega \ cdot \ deg \ eta} \ cdot \ eta \ wedge \ omega;}$

missä merkitsee d: n astetta . ts. jos a-muoto on, niin on . Vastaavasti kahden parittoman asteen muodon tuote on anti-kommutatiivinen ja kommutatiivinen kaikissa muissa yhdistelmissä. ${\ displaystyle \ deg \ omega}$${\ displaystyle \ omega,}$${\ displaystyle \ omega}$${\ displaystyle k}$${\ displaystyle \ deg \ omega = k}$

Esimerkkejä

• Tasaiset toiminnot ovat 0-muotoja.
• Pfaffin muodot ovat 1-muotoja.

Koordinaattien edustus

Olkoon se ulotteinen differentiable moninaiset. Olkaamme myös olettaa paikallinen koordinaatisto (kartta) . Sitten ${\ displaystyle M}$${\ displaystyle n}$${\ displaystyle (U, x)}$

${\ displaystyle B = \ {\ mathrm {d} x_ {i_ {1}} | _ {p} \ wedge \ ldots \ wedge \ mathrm {d} x_ {i_ {k}} | _ {p} \ {\ iso |} \ i_ {1} <\ ldots <i_ {k} \}}$

pohjana , jossa on yhteensä ero on nnen koordinaatiston funktion . Toisin sanoen lineaarinen muoto on se, jolla kartoitetaan emäksen perusvektori vektorille 1 ja kaikki muut 0: lle. ${\ displaystyle \ Lambda ^ {k} (T_ {p} ^ {*} M).}$${\ displaystyle \ mathrm {d} x_ {i}}$${\ displaystyle i}$${\ displaystyle x_ {i}}$${\ displaystyle \ mathrm {d} x_ {i} | _ {p}}$${\ displaystyle T_ {p} (M)}$${\ displaystyle i}$${\ displaystyle \ textstyle {\ frac {\ partitali {\ partituali x_ {1}}} | _ {p}, \ ldots, {\ frac {\ partial} {\ osittainen x_ {n}}} | _ {p }}$

Jokaisella differentiaalilomakkeella on ainutlaatuinen esitys kaikilla kartoilla${\ displaystyle \ omega \ sisään \ Omega ^ {k} (M)}$${\ displaystyle (U, x)}$

${\ displaystyle \ omega | _ {U} = \ summa _ {1 \ leq i_ {1} <\ ldots <i_ {k} \ leq n} a_ {i_ {1}, \ ldots, i_ {k}} \ , \ mathrm {d} x_ {i_ {1}} \ wedge \ ldots \ wedge \ mathrm {d} x_ {i_ {k}}}$

sopivilla eriytettävillä toiminnoilla ${\ displaystyle a_ {i_ {1}, \ ldots, i_ {k}}.}$

Koordinaattiesitys osoittaa, että ainoa differentiaalimuoto on nollamuodolle . ${\ displaystyle k> n}$${\ displaystyle \ omega = 0}$

Ulkoinen johdannainen

Ulompi johdannainen on operaattori, joka määrittää differentiaalimuodon differentiaalimuodolle. Jos tarkastellaan sitä differentiaalimuotojen joukossa , eli sileiden funktioiden joukossa, ulompi johdannainen vastaa funktioiden tavanomaista johdannaista . ${\ displaystyle k}$${\ displaystyle (k + 1)}$${\ displaystyle 0}$

määritelmä

Ulompi johdannainen -muoto tulee induktiivinen käyttäen Lie johdannaista ja Cartan kaava${\ displaystyle \ mathrm {d} \ omega}$${\ displaystyle k}$${\ displaystyle \ omega}$

${\ displaystyle {\ mathcal {L}} _ {X} = i_ {X} \ circ \ mathrm {d} + \ mathrm {d} \ circ i_ {X}}$

Ovat määriteltyjä; on vektorikenttä, Lie-johdannainen ja substituutio${\ displaystyle X}$${\ displaystyle {\ mathcal {L}} _ {X}}$${\ displaystyle i_ {X}}$${\ displaystyle X.}$

Esimerkiksi, jos on 1-muotoinen, niin on ${\ displaystyle \ omega}$

${\ displaystyle ({\ mathcal {L}} _ {X} \ omega) (Y) = {\ mathcal {L}} _ {X} (\ omega (Y)) - \ omega ({\ mathcal {L} } _ {X} (Y)) = X \ omega (Y) - \ omega ([X, Y])}$

ja

${\ displaystyle ((\ mathrm {d} \ circ i_ {X}) \ omega) (Y) = (\ mathrm {d} (\ omega (X))) (Y) = Y \ omega (X),}$

niin

${\ displaystyle \ mathrm {d} \ omega (X, Y) = X \ omega (Y) -Y \ omega (X) - \ omega ([X, Y])}$

vektorikentille ; Lie kiinnike tarkoittaa . ${\ displaystyle X, Y}$${\ displaystyle [X, Y]}$

Yleinen kaava on

${\ displaystyle {\ begin {array} {rcl} \ mathrm {d} \ omega (X_ {0}, \ ldots, X_ {k}) & = & \ summa _ {i = 0} ^ {k} (- 1) ^ {i} X_ {i} \ omega (X_ {0}, \ ldots, {\ hat {X}} _ {i}, \ ldots, X_ {k}) + \\ [0.5em] && + \ sum _ {0 \ leq i <j \ leq k} (- 1) ^ {i + j} \ omega ([X_ {i}, X_ {j}], X_ {0}, \ ldots, {\ hattu {X}} _ {i}, \ ldots, {\ hat {X}} _ {j}, \ ldots, X_ {k}) \ ,; \ end {array}}}$

symbolin katto tarkoittaa , että vastaava argumentti on jätettävä pois. ${\ displaystyle {\ hattu {}}}$${\ displaystyle {\ hattu {X}} _ {i}}$

ominaisuudet

Ulommalla johdannaisella on seuraavat ominaisuudet:

• Ulkoinen johdannainen on antijohdannainen . Eli on -linear ja Leibnizin sääntö pätee${\ displaystyle \ mathrm {d}}$${\ displaystyle \ mathbb {R}}$${\ displaystyle \ alpha \ sisään \ Omega ^ {k} (U), \ beta \ in \ Omega ^ {l} (U)}$

${\ displaystyle \ mathrm {d} (\ alpha \ wedge \ beta) = \ mathrm {d} \ alpha \ wedge \ beta + (- 1) ^ {k} \ alpha \ wedge \ mathrm {d} \ beta.}$

• Olkoon sitten ulompi johdannainen sopusoinnussa kokonaiseron kanssa .${\ displaystyle f \ muodossa C ^ {\ infty} (U),}$
• ${\ displaystyle \ mathrm {d} ^ {2} = \ mathrm {d} \ circ \ mathrm {d} = 0}$
• Ulompi johdannainen noudattaa rajoituksia. Anna sen olla auki ja seuraavaa: Ulkoista johdannaista kutsutaan siksi myös paikalliseksi operaattoriksi.${\ displaystyle U \ osajoukko V \ osajoukko M}$${\ displaystyle \ alpha \ sisään \ Omega ^ {k} (V).}$${\ displaystyle \ mathrm {d} (\ alpha | _ {U}) = (\ mathrm {d} \ alpha) | _ {U}.}$

Nämä neljä ominaisuutta kuvaavat täysin ulkoista johdannaista. Tämä tarkoittaa, että yllä oleva empiirinen kaava voidaan johtaa näistä ominaisuuksista. Jos lasket ulkoisella johdannaisella, haluat mieluummin laskea johdannaisen ominaisuuksilla ja välttää yllä olevaa kaavaa.

Ulkoisen johdannaisen koordinaattiesitys

Differentiaalimuodon ulompi johdannainen

${\ displaystyle \ omega = \ summa _ {1 \ leq i_ {1} <\ ldots <i_ {k} \ leq n} a_ {i_ {1}, \ ldots, i_ {k}} (x) \ cdot \ mathrm {d} x_ {i_ {1}} \ wedge \ ldots \ wedge \ mathrm {d} x_ {i_ {k}}}$

koordinaattien edustuksessa on

${\ displaystyle \ mathrm {d} \ omega = \ summa _ {1 \ leq i_ {1} <\ ldots <i_ {k} \ leq n} \ mathrm {d} a_ {i_ {1}, \ ldots, i_ {k}} \ wedge \ mathrm {d} x_ {i_ {1}} \ wedge \ ldots \ wedge \ mathrm {d} x_ {i_ {k}}}$

kerrointoimintojen kokonaiserojen kanssa

${\ displaystyle \ mathrm {d} a_ {i_ {1}, \ ldots, i_ {k}} = \ summa _ {j = 1} ^ {n} {\ frac {\ osittainen a_ {i_ {1}, \ ldots, i_ {k}}} {\ osittainen x_ {j}}} \ mathrm {d} x_ {j}}$.

Tulosta ilmaisujen ilmaisemiseksi uudelleen standardipohjan kautta ovat identiteetit

${\ displaystyle \ mathrm {d} x_ {i} \ wedge \ mathrm {d} x_ {j} = - \ mathrm {d} x_ {j} \ wedge \ mathrm {d} x_ {i}}$

ja

${\ displaystyle \ mathrm {d} x_ {i} \ wedge \ mathrm {d} x_ {i} = 0}$

tärkeä.

esimerkki

for true ${\ displaystyle n = 2, k = 1}$

${\ displaystyle {\ begin {tasattu} \ mathrm {d} (a_ {1} \ cdot \ mathrm {d} x_ {1} + a_ {2} \ cdot \ mathrm {d} x_ {2}) & = \ mathrm {d} a_ {1} \ wedge \ mathrm {d} x_ {1} + \ mathrm {d} a_ {2} \ wedge \ mathrm {d} x_ {2} \\ [0.5em] & = \ vasen ({\ frac {\ osittainen a_ {1}} {\ osittain x_ {1}}} \ matrm {d} x_ {1} + {\ frac {\ osaa a_ {1}} {\ osallinen x_ {2}} } \ mathrm {d} x_ {2} \ oikea) \ wedge \ mathrm {d} x_ {1} + \ vasen ({\ frac {\ partis a_ {2}} {\ osittain x_ {1}}} \ mathrm {d} x_ {1} + {\ frac {\ osittainen a_ {2}} {\ osittain x_ {2}}} \ mathrm {d} x_ {2} \ oikea) \ kiila \ matrm {d} x_ {2 } \\ [0.5em] & = {\ frac {\ osittainen a_ {1}} {\ osittain x_ {1}}} \ cdot \ mathrm {d} x_ {1} \ kiila \ matrm {d} x_ {1 } + {\ frac {\ osittainen a_ {1}} {\ osittain x_ {2}}} \ cdot \ mathrm {d} x_ {2} \ kiila \ matrm {d} x_ {1} + {\ frac {\ osittainen a_ {2}} {\ osittain x_ {1}}} \ cdot \ mathrm {d} x_ {1} \ kiila \ matrm {d} x_ {2} + {\ frac {\ osittainen a_ {2}} { \ parts x_ {2}}} \ cdot \ mathrm {d} x_ {2} \ wedge \ mathrm {d} x_ {2} \\ [0.5em] & = \ left ({\ frac {\ osittainen a_ {2 }} {\ partituali x_ {1}}} - {\ frac {\ osittainen a_ {1}} {\ ositettu x_ {2}}} \ oikea) \ cdot \ mathrm {d} x_ {1} \ kiila \ mathrm {d} x_ {2}. \ end {tasattu}}}$

Yleensä sovelletaan 1-muodon ulompaa johdannaista

${\ displaystyle \ mathrm {d} \ vasen (\ summa _ {i = 1} ^ {n} a_ {i} \ cdot \ mathrm {d} x_ {i} \ oikea) = \ summa _ {1 \ leq i <j \ leq n} \ vasen ({\ frac {\ partitu a_ {j}} {\ osittain x_ {i}}} - {\ frac {\ osittainen a_ {i}} {\ osittain x_ {j}}} \ right) \ cdot \ mathrm {d} x_ {i} \ wedge \ mathrm {d} x_ {j}}$

Ja kertoimien ulomman johdannainen 1-muoto muodostaa pyörimisen vektorin muodostettu kertoimet 1-muodossa. ${\ displaystyle n = 3}$

Lisäoperaatiot differentiaalimuodoilla

Sisäinen tuote

Antaa olla sileä vektorikenttä. Sisäinen tuote on lineaarinen kartta ${\ displaystyle X \ in T (M)}$

${\ displaystyle i_ {X} \ kaksoispiste \ Omega ^ {k} (M) \ - \ Omega ^ {k-1} (M),}$

mennessä

${\ displaystyle \ omega \ mapsto \ omega (X, \ cdot, \ ldots, \ cdot)}$

annettu on. Tämä tarkoittaa sitä, että sisemmän tuote kartoittaa muoto on muoto, jonka arvioidaan muoto on kiinteä vektori kenttä . Tämä kartoitus on analogia tensorikartiosta differentiaalimuotojen tilassa. Siksi tätä operaatiota kutsutaan joskus englanniksi "supistumiseksi". ${\ displaystyle k}$${\ displaystyle \ omega}$${\ displaystyle (k-1)}$${\ displaystyle X}$

Sisäinen tuote on antijohdannainen . Toisin sanoen ja Leibnizin sääntö pätee${\ displaystyle i_ {X}}$${\ displaystyle \ omega \ sisään \ Omega ^ {k} (M)}$${\ displaystyle \ nu \ in \ Omega ^ {l} (M)}$

${\ displaystyle i_ {X} (\ omega \ wedge \ nu) = (i_ {X} \ omega) \ wedge \ nu + (- 1) ^ {k} \ omega \ wedge (i_ {X} \ nu). }$

Koskee myös sisempää tuotetta ${\ displaystyle i_ {X} \ circ i_ {X} = 0.}$

Paluukuljetukset (pullback) differentiaalimuodoista

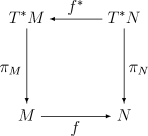
Jos on sileä kartoitus välillä differentioituva pakosarjat , sitten muodossa noutaa määritellään seuraavasti: ${\ displaystyle f \ kaksoispiste M \ - N}$${\ displaystyle \ omega \ sisään \ Omega ^ {k} (N)}$${\ displaystyle f}$ ${\ displaystyle (f ^ {*} \ omega) \ in \ Omega ^ {k} (M)}$

${\ displaystyle (f ^ {*} \ omega) (X_ {1}, \ ldots, X_ {k}): = \ omega (\ mathrm {d} f (X_ {1}), \ ldots, \ mathrm { d} f (X_ {k}))}}$

Se johtuu johdannaisten indusoidusta kartasta , joka tunnetaan nimellä "työntö eteenpäin". Nosto on yhteensopiva ulkoisen viemärin ja ulkoisen tuotteen kanssa: ${\ displaystyle df \ kaksoispiste TM \ TN: hen}$${\ displaystyle f}$

• ${\ displaystyle f ^ {*} (\ mathrm {d} \ omega) = \ mathrm {d} (f ^ {*} \ omega)}$

(kirjoitettu tarkemmin: vasemmalla puolella , sitä vasten oikealla puolella ) ja${\ displaystyle \ mathrm {d} = \ mathrm {d} ^ {(N)}}$${\ displaystyle \ mathrm {d} = \ mathrm {d} ^ {(M)}}$

• ${\ displaystyle f ^ {*} (\ omega \ wedge \ eta) = (f ^ {*} \ omega) \ wedge (f ^ {*} \ eta)}$

kaikille ${\ displaystyle \ omega, \ eta \ sisällä \ Omega ^ {pback} (N)}$

Erityisesti kartoitus De Rham -kohomologisten ryhmien välillä (katso alla) ${\ displaystyle f}$

${\ displaystyle f ^ {pback} \ kaksoispiste \ mathrm {H} _ {\ mathrm {dR}} ^ {k} (N) \ longrightarrow \ mathrm {H} _ {\ mathrm {dR}} ^ {k} ( M),}$

Kiinnitä huomiota vastakkaisen nuolen suunnan kääntymiseen ("vetäytyminen", "kohomologia" homologian sijaan). ${\ displaystyle f \ kaksoispiste M \ - N}$

Kaksoismuoto ja tähtioperaattori

Ulkomuotoja tarkastellaan -dimensionaalisessa tilassa, jossa sisäinen tuote (metrinen) on määritelty niin, että avaruuden ortonormaalipohja voidaan muodostaa. Muoto, joka on kaksinkertainen ulkoiseen astemuotoon tässä -ulotteisessa tilassa, on -muoto ${\ displaystyle n}$${\ displaystyle e_ {i}}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle (nk)}$

${\ displaystyle * (e_ {1} \ wedge e_ {2} \ wedge \ ldots \ wedge e_ {k}) = e_ {k + 1} \ wedge e_ {k + 2} \ wedge \ ldots \ wedge e_ {n }.}$

Molemmat osapuolet on kirjoitettu suuntautuneessa muodossa. Kaksoismuoto määritetään muodollisesti (Hodge) -operaattorilla. Erityisesti kolmiulotteisen euklidisen avaruuden differentiaalimuodoille seuraavat tulokset: ${\ displaystyle *}$

${\ displaystyle * \ mathrm {d} x = \ mathrm {d} y \ wedge \ mathrm {d} z}$

${\ displaystyle * \ mathrm {d} y = \ mathrm {d} z \ wedge \ mathrm {d} x}$

${\ displaystyle * \ mathrm {d} z = \ mathrm {d} x \ wedge \ mathrm {d} y}$

1 lomakkeen kanssa . Otettiin huomioon, että suuntautunut järjestys on täällä ja (suhdannevaihtelut sisään ). ${\ displaystyle dx, dy, dz}$${\ displaystyle (y, z), (z, x)}$${\ displaystyle (x, y)}$${\ displaystyle (x, y, z)}$

Symboli on tarkoitus korostaa sitä seikkaa, että on olemassa sisäinen tuote tilaan lomakkeiden taustalla tilaa , koska se on mahdollista kirjoittaa kaksi muotoja ja tilavuus muoto ja kiinteä ${\ displaystyle *}$${\ displaystyle M}$${\ displaystyle \ alpha \ wedge * \ beta}$${\ displaystyle k}$${\ displaystyle \ alfa}$${\ displaystyle \ beta}$

${\ displaystyle (\ alpha, \ beta) = \ int _ {M} \ alpha \ wedge * \ beta}$

palauttaa reaaliluvun. Lisäyksellä Dual osoittaa, että kaksinkertainen soveltaminen on -muotoa tuloksia -muodossa uudelleen - paitsi merkkiä , jotka on otettava huomioon erikseen. Tarkemmin sanottuna seuraava koskee -muotoa a- ulotteisessa avaruudessa, jonka metrikalla on allekirjoitus ( euklidisessa avaruudessa, Minkowskin avaruudessa): ${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle s}$${\ displaystyle s = + 1}$${\ displaystyle s = -1}$

${\ displaystyle ** \ alpha = (- 1) ^ {k (nk)} s \; \ alpha}$

Edellä on esitetty, kuinka 3-ulotteinen euklidinen avaruus 2-muoto tulokset kanssa ulkoisen johtaminen 1-muoto komponenttien kanssa pyörimisen vektorin vektori analyysin kertoimiksi. Nämä kaksi muodostavat voit -operator nyt virallisesti suoraan yhtenä muotona ( punainen vektori) kirjoittaa: . Vastaavasti operaattoria käytetään "kääntämään" edellä muotoiltu Stokesin lause vektorianalyysimuotoon. ${\ displaystyle \ alfa}$${\ displaystyle d \ wedge \ alpha}$${\ displaystyle *}$${\ displaystyle * (d \ wedge \ alpha)}$${\ displaystyle *}$

De Rham -kohomologia

Alkaen valmistui algebran , yhdessä ulomman johdannaisen, joka on keimailija kompleksi voidaan rakentaa. Tätä verrataan sitten homologisen algebran tavanomaisiin menetelmiin, joista yksi kohomologia määritellään. Georges de Rham pystyi osoittamaan, että tämä hänen nimensä mukainen cohomology-teoria on yhtäpitävä singulaarisen kohomologian kanssa . De Rham -kohomologian määrittelemiseksi määritetään ensin tarkan ja suljetun differentiaalimuodon termit: ${\ displaystyle \ Omega (U)}$

Tarkat ja suljetut muodot

A -muotoa kutsutaan suljetuksi, jos se on voimassa; sitä kutsutaan tarkalleen, onko olemassa sellainen -muoto , joka pitää. Kaavan takia jokainen tarkka muoto on suljettu. On huomattava, että läheisyys, toisin kuin täsmällisyys, on paikallinen ominaisuus: Jos on avoin kansi on sitten -muoto on suljettu, jos ja vain jos rajoitus on on suljettu jokaiselle . ${\ displaystyle k}$${\ displaystyle \ omega}$${\ displaystyle \ mathrm {d} \ omega = 0}$${\ displaystyle (k-1)}$${\ displaystyle \ eta}$${\ displaystyle \ omega = \ mathrm {d} \ eta}$${\ displaystyle \ mathrm {d} \ mathrm {d} \ eta = 0}$${\ displaystyle \ {V _ {\ alpha} \}}$${\ displaystyle U,}$${\ displaystyle k}$${\ displaystyle \ omega}$${\ displaystyle \ omega}$${\ displaystyle V _ {\ alpha}}$${\ displaystyle \ alfa}$

De Rham -kohomologiset ryhmät

Tekijä tila

(Aseta kaikki suljetut lomakkeet päälle ) (aseta kaikki tarkat lomakkeet päälle )${\ displaystyle k}$${\ displaystyle U}$${\ displaystyle {\ iso /}}$${\ displaystyle k}$${\ displaystyle U}$

on nimeltään -th De Rham -kohomologinen ryhmä. Se sisältää tietoa globaalista topologisesta rakenteesta${\ displaystyle k}$ ${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {k} (U).}$${\ displaystyle U.}$

Poincarén lemma

Poincarén lemman mukaan varten ja tähti alueille . Yleisemmin, selvitys tämän Lemman koskee kokoonsupistettavassa auki osajoukot Todiste on rakentava, i. Toisin sanoen laaditaan selkeitä esimerkkejä, mikä on erittäin tärkeää sovelluksille. Huomaa, että se koostuu paikallisesti vakio-funktioista , koska määritelmän mukaan ei ole tarkkoja 0-muotoja. Joten se on kaikille${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {k} (U) = 0}$${\ displaystyle k> 0}$ ${\ displaystyle U}$${\ displaystyle U}$${\ displaystyle \ mathbb {R} ^ {n}.}$${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {0} (U)}$${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {0} (U) \ not = 0}$${\ displaystyle U \ neq \ lakkaus.}$

Jos se on suljettu ja tarkka, se seuraa ${\ displaystyle \ omega}$${\ displaystyle \ eta = \ mathrm {d} \ eta '}$

${\ displaystyle \ omega \ wedge \ eta = \ omega \ wedge \ mathrm {d} \ eta '= (- 1) ^ {\ deg \ omega} \ mathrm {d} (\ omega \ wedge \ eta') \, .}$

Sama pätee, jos se on tarkka ja suljettu. Joten on indusoituja kartoituksia ${\ displaystyle \ omega}$${\ displaystyle \ eta}$

${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {k} (U) \ kertaa H _ {\ mathrm {dR}} ^ {m} (U) \ longrightarrow \ mathrm {H} _ { \ mathrm {dR}} ^ {k + m} (U).}$

Esimerkki elektrodynamiikasta

In electrodynamics mikä merkitsee Aine Poincarén , että kunkin parin sähkömagneettisten kenttien, että kaksivaiheinen vuorotellen ero muodossa neljän ulotteinen Minkowskin tila voidaan tiivistää, yksivaiheinen vektori potentiaali muodossa , jossa on olemassa, niin kutsuttu "neljä -potentiaalinen ", katso myös nelivektori . Virta- ja varaustiheydet voidaan myös yhdistää nelivektorin tai vastaavan 3-muodon muodostamiseksi . ${\ displaystyle {\ vec {E}}, {\ vec {B}}}$${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {F} = \ mathrm {d} \ mathbf {A}}$${\ displaystyle \ mathbf {j}}$

Relativistinen Maxwellin yhtälöt ja electrodynamics on neljä-ulotteinen avaruus-aika jakotukki (metriset ja determinantti metrisen , jolloin tässä tietenkin allekirjoitus Minkowskin tila on läsnä, esimerkiksi varten mukaisen määritelmän putkielementin ) ovat esimerkiksi käyttämällä tätä symboliikkaa: ${\ displaystyle M}$${\ displaystyle g _ {\ alfa, \ beta}}$${\ displaystyle g}$${\ displaystyle \ mathrm {diag} (+ 1, -1, -1, -1)}$${\ displaystyle \ alpha = 0,1,2,3,}$ ${\ displaystyle \ mathrm {ds}}$

${\ displaystyle \ mathrm {d} \ mathbf {F} = 2 (\ osal _ {\ gamma} F _ {\ alfa \ beta} + \ osittainen _ {\ beta} F _ {\ gamma \ alfa} + \ osittainen _ {\ alpha} F _ {\ beta \ gamma}) \ mathrm {d} \, x ^ {\ alpha} \ wedge \ mathrm {d} \, x ^ {\ beta} \ wedge \ mathrm {d} \ , x ^ {\ gamma} = 0}$

(niin kutsuttu Bianchi-identiteetti ) ja

${\ displaystyle \ mathrm {d} (* \ mathbf {F}) = {F ^ {\ alpha \ beta}} _ {; \ alpha} {\ sqrt {-g}} \, \ epsilon _ {\ beta \ gamma \ delta \ eta} \ mathrm {d} \, x ^ {\ gamma} \ wedge \ mathrm {d} \, x ^ {\ delta} \ wedge \ mathrm {d} \, x ^ {\ eta} = \ mathbf {j}}$

sähkömagneettisen kentän tensorin kanssa 2-muodossa

${\ displaystyle \ mathbf {F} = F _ {\ alpha \ beta} \, \ mathrm {d} \, x ^ {\ alpha} \ wedge \ mathrm {d} \, x ^ {\ beta} \ ,, }$

z. B. kanssa vektorin komponentti magneettisen induktion ja nykyisen (kirjoitetaan 3-muoto) ${\ displaystyle F_ {1,2} = B_ {z}}$${\ displaystyle z}$

${\ displaystyle \ mathbf {j} = j ^ {\ alpha} {\ sqrt {-g}} \, \ epsilon _ {\ alpha \ beta \ gamma \ delta} \ mathrm {d} \, x ^ {\ beta } \ wedge \ mathrm {d} \, x ^ {\ gamma} \ wedge \ mathrm {d} \, x ^ {\ delta}.}$

Tässä on symmetrisoitumisen vastainen symboli ( Levi-Civita-symboli ), ja puolipiste tarkoittaa kovariaanssijohdannaista . Kuten tavallista, lisätään kaksi kertaa esiintyvät indeksit ( Einsteinin summasopimus ) ja käytetään luonnollisia yksiköitä (valon nopeus korvataan ). Operaattoria käyttämällä neljän Maxwell-yhtälön toinen joukko voidaan vaihtoehtoisesti kirjoittaa 1-muodolla virralle. Maxwell-yhtälöistä voidaan nähdä se ja noudattaa hyvin erilaisia ​​yhtälöitä elektrodynamiikassa, joten kaksinaisuus ei ole tämän teorian symmetria. Tämä johtuu siitä, että kaksinaisuus vaihtaa sähköisiä ja magneettikenttiä, mutta elektrodynamiikassa magneettisia monopoleja ei tunneta. Toisaalta ilmaisevilla Maxwell-yhtälöillä on kaksoissymmetria. ${\ displaystyle \ epsilon _ {\ alfa \ beta \ gamma \ delta}}$${\ displaystyle c}$${\ displaystyle 1}$${\ displaystyle *}$${\ displaystyle \ mathbf {F}}$${\ displaystyle * \ mathbf {F}}$${\ displaystyle \ mathbf {j} \ equiv 0}$

Mahdollinen muoto on vain yksiselitteinen lukuun ottamatta yhtä lisäainetta lisäksi : ja tulos samassa kanssa kalibroinnin muotoon , joka on täytetty, mutta muuten mielivaltaisia. Tätä niin sanottua kalibrointivapautta voidaan käyttää ylimääräisten rajoitusten täyttämiseen tietyissä kohdissa. Esimerkiksi elektrodynamiikassa vaaditaan, että ns. Lorenzin lisäehto ( Lorenzin kalibrointi ) pätee kaikkialle ; tämä ehto on yksinkertainen neljässä komponentissa . Tämä "kalibrointikiinnitys" johtaa lopulta ns. "Hidastettuun potentiaaliin" ainutlaatuisena ratkaisuna kaikkiin neljään Maxwell-yhtälöön: ${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathrm {d} \ chi}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {A} + \ mathrm {d} \ chi}$${\ displaystyle \ mathbf {F},}$ ${\ displaystyle \ chi}$${\ displaystyle \ mathrm {d} (\ mathrm {d} \ chi) \ equiv 0}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathrm {d} (* \ mathbf {A}) = 0}$${\ displaystyle \ osittainen _ {\ nu} A ^ {\ nu} = 0}$

${\ displaystyle A ^ {\ nu} (\ mathbf {r}, t) = \ int \, {\ frac {j ^ {\ nu} (\ mathbf {r '}, t - {\ frac {| \ mathbf {r} - \ mathbf {r '} |} {c}})} {4 \ pi | \ mathbf {r} - \ mathbf {r'} |}}} \, \ mathrm {d} ^ {3} r '}$

Kun siirrytään dualiin, on huomattava, että et ole tekemisissä sen kanssa, vaan sen kanssa, jolla on erilainen metriikka, nimittäin Minkowski-metriikka . Lorentz-muunnosten invariantti linjaelementti on paikka, jossa ero on oikea aika ja summa-sopimusta käytettiin. Samanaikaiset ja sopivat neljän vektorin komponentit eroavat nyt. On totta , mutta sekä${\ displaystyle \ mathbb {R} ^ {4},}$${\ displaystyle \ mathbb {M} ^ {4}}$${\ displaystyle \ mathrm {d} s ^ {2} = - c ^ {2} \ mathrm {d} \ tau ^ {2} = dx ^ {2} + dy ^ {2} + dz ^ {2} - c ^ {2} dt ^ {2} = - \ mathrm {d} x _ {\ nu} \ mathrm {d} x ^ {\ nu},}$${\ displaystyle \ mathrm {d} \ tau}$${\ displaystyle + \ mathrm {d} x_ {0} \ equiv + \ mathrm {d} x ^ {0} = c \, dt,}$${\ displaystyle - \ mathrm {d} x_ {1} \ equiv + \ mathrm {d} x ^ {1} = dx,}$ ${\ displaystyle - \ mathrm {d} x_ {2} \ equiv + \ mathrm {d} x ^ {2} = dy}$${\ displaystyle - \ mathrm {d} x_ {3} \ equiv + \ mathrm {d} x ^ {3} = dz.}$

Integrointiteoria

suuntautuminen

Jos tämä on nimi -muoto on joka ei missään vaiheessa katoaa, suunta on yhdessä sellaisessa muodossa, on nimeltään suunnattu. Suunta määrittelee tangentiaalisten ja kotangenttitilojen orientaatiot: Kotangenttitilan pohja pisteessä on positiivinen, jos ${\ displaystyle n = \ himmeä U,}$${\ displaystyle n}$${\ displaystyle U,}$${\ displaystyle U.}$ ${\ displaystyle U}$${\ displaystyle \ alfa}$${\ displaystyle \ eta _ {1}, \ ldots, \ eta _ {n}}$${\ displaystyle p}$

${\ displaystyle \ alpha _ {p} = a \ cdot \ eta _ {1} \ wedge \ ldots \ wedge \ eta _ {n}}$

positiivisella luvulla . Tangenttitilan pohja pisteessä on positiivisesti suuntautunut, jos ${\ displaystyle a}$${\ displaystyle X_ {1}, \ ldots, X_ {n}}$${\ displaystyle p}$

${\ displaystyle \ alpha (X_ {1}, \ ldots, X_ {n})> 0}$

sovelletaan.

Kahden suuntauksen sanotaan olevan samanarvoisia, jos ne eroavat toisistaan ​​vain yleisesti positiivisen tekijän perusteella; tämä ehto vastaa saman suunnan määrittelemistä jokaisella tangentti- tai kotangenttitilalla.

Jos kytkettynä on joko ollenkaan tai täsmälleen kaksi ekvivalenssiluokkia. ${\ displaystyle U}$

${\ displaystyle U}$tarkoittaa suuntautuvaa, jos on suunta . ${\ displaystyle U}$

Eri muotojen integrointi

Olkoon se uudelleen ja oletamme , että suunta on valittu. Sitten on kanoninen integraali ${\ displaystyle n = \ himmeä U,}$${\ displaystyle U}$

${\ displaystyle \ int _ {U} \ omega}$

for -forms on avoin osajoukko , vakiokoordinaattofunktiot ovat im ja on ${\ displaystyle n}$${\ displaystyle \ omega.}$${\ displaystyle U}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle x_ {1}, \ ldots, x_ {n}}$${\ displaystyle \ mathbb {R} ^ {n}}$

${\ displaystyle \ omega = f \, \, \ mathrm {d} x_ {1} \ wedge \ ldots \ wedge \ mathrm {d} x_ {n},}$

niin:

${\ displaystyle \ int _ {U} \ omega = \ int _ {U} f (x_ {1}, \ pisteitä, x_ {n}) \, \, \ mathrm {d} x_ {1} \ ldots \ mathrm {d} x_ {n}}$

Oikealla oleva integraali on tavallinen Lebesgue-integraali im${\ displaystyle \ mathbb {R} ^ {n}.}$

Jos ulotteinen suuntautunut pakosarja on auki ja kartta, sitten yksi määrittelee ${\ displaystyle M}$${\ displaystyle n}$${\ displaystyle U \ osajoukko M}$${\ displaystyle \ phi \ kaksoispiste U \ to \ mathbb {R} ^ {n}}$

${\ displaystyle \ int _ {U} \ omega = \ int _ {\ phi (U)} (\ phi ^ {- 1}) ^ {*} \ omega}$

integraalina -muodosta kartan alueella . Ero muoto on tuotu takaisin avoimeen osajoukon kanssa parametroinnin ja ja sitten integroidaan mukaan edellä esitettyä määritelmää. Vuodesta muutosta lauseen tästä seuraa, että tämä määritelmä on muuttumaton koordinoida muutoksia. ${\ displaystyle n}$${\ displaystyle \ omega}$${\ displaystyle U}$${\ displaystyle \ omega}$${\ displaystyle \ phi ^ {- 1} \ kaksoispiste \ phi (U) \ - U}$${\ displaystyle U}$${\ displaystyle \ phi (U) \ osajoukko \ mathbb {R} ^ {n}}$

Jos, yleisesti, on mitattavissa osajoukko , sitten yksi määrittelee ${\ displaystyle B}$${\ displaystyle U}$

${\ displaystyle \ int _ {B} \ omega = \ int _ {U} \ chi _ {B} \ omega}$

jossa karakteristinen funktio , d. ts. asetetaan nollan ulkopuolelle . ${\ displaystyle \ chi _ {B}}$${\ displaystyle \ omega}$${\ displaystyle B}$

Hajotusta voidaan käyttää integraalin määrittelemiseksi kokonaisuudeksi${\ displaystyle M}$

${\ displaystyle M = \ bigcup _ {j = 1} ^ {\ infty} M_ {j}}$

voidaan valita lukemattomaan määrään pareittain irtoavia mitattavia osajoukkoja , niin että kukin sisältyy kokonaan yhteen kartan alueeseen. Joten lyöt vetoa ${\ displaystyle M_ {j}}$${\ displaystyle M_ {j}}$${\ displaystyle U_ {j}}$

${\ displaystyle \ int _ {M} \ omega = \ summa _ {j = 1} ^ {\ infty} \ int _ {M_ {j}} \ omega}$.

Seuraava muunnoslause koskee differentiaalimuotojen integraaleja: Jos on suuntaa säilyttävä diffeomorfismi , pätee sitten${\ displaystyle f \ kaksoispiste M \ - N}$${\ displaystyle \ omega \ sisään \ Omega ^ {n} (N)}$

${\ displaystyle \ int _ {N} \ omega = \ int _ {M} f ^ {*} \ omega}$

jossa on haettu muodossa . ${\ displaystyle M}$${\ displaystyle f ^ {*} \ omega}$

Stokesin lause

Jos kompakti, suuntautunut- ulotteinen erottuva jakotukki, jolla on raja ja joka on varustettu indusoidulla orientaatiolla, pätee jokaiseen -muotoon${\ displaystyle M}$${\ displaystyle n}$ ${\ displaystyle \ osittainen M}$${\ displaystyle \ osittainen M}$${\ displaystyle (n-1)}$${\ displaystyle \ omega}$

${\ displaystyle \ int _ {M} \ mathrm {d} \ omega = \ int _ {\ osittainen M} \ omega.}$

Tämä lause on kauaskantoinen yleistys differentiaali- ja integraalilaskennan päälauseesta . Se sisältää Gaussin integraalilauseen ja Stokesin klassisen integraalilauseen erikoistapauksina .

Jos se on suljettu , se seuraa jokaista tarkkaa -muotoa d. H. for suhdetta ${\ displaystyle M}$ ${\ displaystyle \ osittainen M = \ tyhjennetty,}$ ${\ displaystyle n}$${\ displaystyle \ omega ^ {\ text {tarkka}},}$${\ displaystyle \ omega \ equiv \ omega ^ {\ text {tarkka}} = \ mathrm {d} \ varphi,}$

${\ displaystyle \ int _ {M} \ omega ^ {\ text {tarkka}} = \ int _ {M} \ mathrm {d} \ varphi = \ int _ {\ osittainen M = \ tyhjät}} varphi = 0. }$

Mainitun yhden ominaisuuden selventämiseksi käytetään usein ympyrän integraalilla olevaa formulointia: ${\ displaystyle M}$

${\ displaystyle \ vo _ {M} \ omega ^ {\ text {tarkka}} = 0}$

Integraali tarjoaa kartan

${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {n} (M) \ to \ mathbb {R}.}$

Jos yhteys on muodostettu, tämä kartoitus on isomorfismi . Tämä tuo sinut takaisin De Rham -kohomologiaan (katso yllä). ${\ displaystyle M}$

Esimerkkilaskelmat

Käytössä suorakulmaiset koordinaatit ovat 1-muodossa ${\ displaystyle \ mathbb {R} ^ {3}}$ ${\ displaystyle (x, y, z)}$

${\ displaystyle \ omega = z ^ {2} \, \ mathrm {d} x + 2y \, \ mathrm {d} y + xz \, \ mathrm {d} z}$

ja 2-muotoinen

${\ displaystyle \ nu = z \, \ mathrm {d} z \ wedge \ mathrm {d} x}$

annettu.

Seuraava koskee ulkoista tuotetta:

${\ displaystyle \ omega \ wedge \ nu = z ^ {3} \, \ underbrace {\ mathrm {d} x \ wedge \ mathrm {d} z \ wedge \ mathrm {d} x} _ {= \, 0} + 2yz \, \ underbrace {\ mathrm {d} y \ wedge \ mathrm {d} z \ wedge \ mathrm {d} x} _ {= \, \ mathrm {d} x \ wedge \ mathrm {d} y \ wedge \ mathrm {d} z} + xz ^ {2} \, \ underbrace {\ mathrm {d} z \ wedge \ mathrm {d} z \ wedge \ mathrm {d} x} _ {= \, 0} = 2yz \, \ mathrm {d} x \ wedge \ mathrm {d} y \ wedge \ mathrm {d} z}$

Ulompi johdannainen antaa ${\ displaystyle \ omega}$

${\ displaystyle \ mathrm {d} \ omega = 2z \, \ mathrm {d} z \ wedge \ mathrm {d} x + 2 \, \ mathrm {d} y \ wedge \ mathrm {d} y + (z \ , \ mathrm {d} x + x \, \ mathrm {d} z) \ wedge \ mathrm {d} z = 2z \, \ mathrm {d} z \ wedge \ mathrm {d} xz \, \ mathrm {d } z \ wedge \ mathrm {d} x = z \, \ mathrm {d} z \ wedge \ mathrm {d} x}$,

niin . Erityisesti se on tarkka ja siten suljettu, so. H. . Tämä voidaan todentaa suoraan laskemalla: . ${\ displaystyle \ mathrm {d} \ omega = \ nu}$${\ displaystyle \ nu}$${\ displaystyle \ mathrm {d} \ nu = 0}$${\ displaystyle \ mathrm {d} \ nu = \ mathrm {d} z \ wedge \ mathrm {d} z \ wedge \ mathrm {d} x = 0}$

Lisäksi annetaan sen jälkeen , , ja , , sivustolta haetuissa muodossa: ${\ displaystyle c \ kaksoispiste [0,1] \ - \ mathbb {R} ^ {3}}$${\ displaystyle c (t) = (t ^ {2}, 2t, 1)}$${\ displaystyle x = t ^ {2}}$${\ displaystyle y = 2t}$${\ displaystyle z = 1}$${\ displaystyle \ mathrm {d} x = 2t \, \ mathrm {d} t}$${\ displaystyle \ mathrm {d} y = 2 \, \ mathrm {d} t}$${\ displaystyle \ mathrm {d} z = 0}$${\ displaystyle [0,1]}$

${\ displaystyle c ^ {*} \ omega = 2t \, \ mathrm {d} t + 8t \, \ mathrm {d} t = 10t \, \ mathrm {d} t}$

Käyrän yli integraalille im saadaan näin saatuja tuloksia ${\ displaystyle \ omega}$${\ displaystyle c}$${\ displaystyle \ Gamma = c ([0,1])}$${\ displaystyle \ mathbb {R} ^ {3}}$

${\ displaystyle \ int _ {\ Gamma} \ omega = \ int _ {[0,1]} c ^ {*} \ omega = \ int _ {0} ^ {1} 10t \, \ mathrm {d} t = 5}$.

Jos yksikkö pallo on sisään , niin reuna yksikön pallo on siksi . Stokesin lauseen mukaan meillä on, koska${\ displaystyle S ^ {2} = \ {\ mathbf {x} \ in \ mathbb {R} ^ {3} \ {\ iso |} \ \ | \ mathbf {x} \ | _ {2} = 1 \ }}$${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle S ^ {2}}$ ${\ displaystyle B ^ {3} = \ {\ mathbf {x} \ in \ mathbb {R} ^ {3} \ {\ iso |} \ \ | \ mathbf {x} \ | _ {2} <1 \ }}$${\ displaystyle S ^ {2} = \ osittainen B ^ {3}}$${\ displaystyle \ mathrm {d} \ nu = 0}$

${\ displaystyle \ int _ {S ^ {2}} \ nu = \ int _ {B ^ {3}} \ mathrm {d} \ nu = 0}$.

Esimerkiksi 3-muotoinen voidaan integroida yksikkökuution avulla . Sen integraali on sama kuin kerroinfunktion Lebesgue-integraali : ${\ displaystyle \ omega \ wedge \ nu}$${\ displaystyle W = [0,1] ^ {3}}$${\ displaystyle (x, y, z) \ mapsto 2yz}$

${\ displaystyle \ int _ {W} \ omega \ wedge \ nu = \ int _ {W} 2yz \, \ mathrm {d} x \ wedge \ mathrm {d} y \ wedge \ mathrm {d} z = \ int _ {0} ^ {1} \ int _ {0} ^ {1} \ int _ {0} ^ {1} 2yz \, \ mathrm {d} x \, \ mathrm {d} y \, \ mathrm { d} z = 2 \ cdot \ int _ {0} ^ {1} y \, \ mathrm {d} y \ cdot \ int _ {0} ^ {1} z \, \ mathrm {d} z = {\ frac {1} {2}}}$.

Monimutkaiset differentiaalimuodot

Monimutkaisten differentiaalimuotojen teoriassa tässä esitetty laskenta siirretään monimutkaisiin jakotukkiin . Suurimmaksi osaksi tämä toimii analogisesti tässä kuvattujen muotojen määritelmän kanssa. Kompleksilukujen tapaan kompleksisten differentiaalimuotojen välit muunnetaan kuitenkin kahteen (todellisten) differentiaalimuotojen avaruuteen

${\ displaystyle {\ mathcal {E}} ^ {r} (M) \ cong \ Omega ^ {r, r} (M) = \ Omega ^ {r} (M) \ oplus i \ Omega ^ {r} ( M)}$

purettu. Avaruutta kutsutaan sitten muotojen avaruudeksi . Näihin tiloihin voidaan määritellä kaksi uutta johdannaista analogisesti ulkoisen johdannaisen kanssa. Nämä ovat Dolbeault- kutsutut ja Dolbeault-ristiinoperaattorit, ja samanlainen kuin De Rham -kohomologia voi olla a-ristin-Dolbeault-operaattorin jälleen kohomologian muodossa. Tätä kutsutaan Dolbeault-kohomologiaksi . ${\ displaystyle \ Omega ^ {p, q}}$${\ displaystyle (p, q)}$

Katso myös

Vektori arvostetaan differentiaalilomakkeita

kirjallisuus

• Herbert Amann, Joachim Escher : Analyysi III. 2. painos. Birkhäuser, Basel 2008, ISBN 978-3-7643-8883-6 , XI ja XII luku.
• Henri Cartan : Erot. Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01443-1 .
• Klaus Jänich : Vektorianalyysi. 5. painos. Springer, Berliini / Heidelberg 2005, ISBN 978-3-540-27338-7 .
• Shigeyuki Morita: Eri muotojen geometria. American Mathematical Society 2001, ISBN 0821810456 .
• Harley Flanders : Differentiaalilomakkeet fysiikan sovelluksilla. Academic Press, 1963.
• Harold Edwards : Advanced Calculus - differentiaalimuodon lähestymistapa. Birkhäuser, 1994 (ensimmäinen vuonna 1969).
• Steven H.Weintraub : Differentiaalimuodot - täydennys vektorilaskemaan. Academic Press, 1997.

nettilinkit

• Gunnar Fløystad: Ulkopuolinen algebra ja keskeiset käsitteet matematiikassa. (PDF; 182 kt). Ilmoitukset AMS, osa 62, 2015, nro 4.
• Differential-muoto nLabissa.