Malfatti-ympyrä

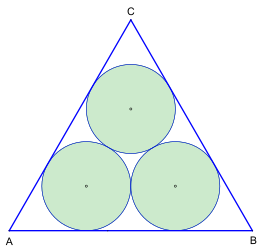
Kolme Malfatti-ympyrää , jotka tunnetaan myöhemmin nimellä Malfatti-ongelma , on nimetty Gianfrancesco Malfattin mukaan , joka ilmoitti rakentamisensa vuonna 1803. Malfatti ympyrät määritetään - riippumatta muoto alkaa kolmio - kolme piireissä on kolmion omaisuutta, että jokainen koskettaa kaksi muuta piireissä ulkopuolelta ja kaksi kolmion sivut sisäpuolelta.

Malfatti oletti virheellisesti, että tämä ympyröiden ominaisuus ratkaisi ongelman, joka aiheutti kolmen ympyrän pakkaamisen kolmioon ilman päällekkäisyyttä siten, että niillä on suurin pinta-ala . Miksi Malfatti-ympyrät eivät pysty ratkaisemaan tätä niin kutsuttua Malfatti-maksimointiongelmaa , ts . Kolmion muotoisen alueen suurin peittävyys kolmella ympyrällä , voidaan nähdä esim. B. voidaan helposti tunnistaa pitkästä kapeasta suorakulmiosta .

Seuraava koskee kolmion ABC Malfatti-ympyrän säteitä:

${\ displaystyle r_ {A} = {\ frac {r} {2 (sa)}} (sr - ({\ overline {IB}} + {\ overline {IC}} - {\ overline {IA}})) }$

${\ displaystyle r_ {B} = {\ frac {r} {2 (sb)}} (sr - ({\ overline {IC}} + {\ overline {IA}} - {\ overline {IB}})) }$

${\ displaystyle r_ {C} = {\ frac {r} {2 (sc)}} (sr - ({\ overline {IA}} + {\ overline {IB}} - {\ overline {IC}})) }$

Se on , että incircle säde ja puoli kehän kolmion. on ympyrän keskipiste ja ovat kolme puolittajaa . ${\ displaystyle r}$${\ displaystyle s}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}, \ omega _ {\ gamma}}$

Historia

Marmori Ongelma
kolmioprisma kolmella kaiverrettu lieriömäistä saraketta sekä yhdeksän mahdolliset kosketuspisteet on Malfatti piireissä

Alkuperäinen Malfatti-ongelma liittyi stereotomian ongelmaan , jonka oletetun ratkaisun Malfatti löysi vuonna 1802 ja julkaisi vuonna 1803 Memoria di Matematica e Fisica della Società Italiana delle Scienze artikkelissa Memoria sopra un problema stereotomico . Artikkelinsa alussa Malfatti muotoilee käsillä olevan tehtävän.

Vapaasti käännettynä se kuuluu:

Mistä tahansa materiaalista, esimerkiksi marmorista valmistetun suorakulmaisen prisman tapauksessa siitä leikataan kolme [pyöreää] sylinteriä samalla korkeudella kuin prisma, mutta suurimmalla mahdollisella kokonaistilavuudella, toisin sanoen siten, että prisman tilavuudesta tulee mahdollisimman vähän jätettä.

Artikkelissaan Memoria sopra un problema stereotomico Malfatti huomauttaa myös, että tämä stereotominen tehtävä voidaan supistaa pinnan geometrian ongelmaksi. Hän määrittelee kolmioon kirjoitettujen ympyröiden, joita nyt kutsutaan Malfatti-ympyröiksi, sijainnin seuraavasti:

Ilmainen käännös

Kun olet antanut kolmion, rakenna siihen kolme ympyrää siten, että jokainen ympyrä on tangentti (toisin sanoen ne koskettavat pistettä) kahden muun ja kolmion kahden sivun kanssa.

Tämän kumoivat kuitenkin vuonna 1992 WA Salgaller ja GA Los, jotka osoittivat, että ratkaisu saavutetaan sen sijaan kirjoittamalla ympyrä, jolla on suurin pinta peräkkäin - kuvataan alla rakennusosassa Salgallerin ja Losin mukaan .

Jo vuonna 1687 Malfatti-rakentamisongelman ratkaisi Jakob I Bernoulli erityistapauksessa (tasakylkinen kolmio), ja myöhemmin Jakob Steiner ja Alfred Clebsch antoivat ratkaisut puhtaasti geometrisesti , jälkimmäisellä oli elliptiset toiminnot (1857, Crelle's Journal). Japanilainen Ajima Naonobu ehdotti myös ratkaisua 30 vuotta ennen Malfattia japanilaisen arkkitehtuurin yhteydessä. Lob ja Richmond osoittivat jo, että Malfattin rakentaminen ei ratkaissut Malfatti-ongelmaa kaikissa tapauksissa tasasivuisten kolmioiden avulla , ja Howard W.Eves vuonna 1965 tutkimuksissa, joissa käytettiin kapeita ja pitkiä kolmioita. Vuonna 1967 Michael Goldbergin essee osoitti jopa, että Malfatin rakentaminen ei koskaan tehnyt tätä. Kuten edellä mainittiin, Salgaller ja Los 1992 toimittivat todisteita tästä.

Geometriset rakenteet

Vuonna 2003 Ingmar Lehmann selitti erilaisia ​​ratkaisuja Malfatti-ongelmaan analyysissään Malfatti-ongelma - aihe lahjakkaiden opiskelijoiden mainostamisessa . Neljä menetelmää kuvataan yksityiskohtaisesti jäljempänä.

Malfatti-rakennus

Malfatti kiertää Malfatin mukaan, laskentakaavio

Vaihtoehto aikaisempiin laskelmiin

Tätä tarkoitusta varten Lehmann johtaa kolme yhtälöä Pythagorean lauseen ja kolmiojen samankaltaisuuden avulla , joiden ratkaisut tarjoavat tangenttisegmentit ja . ${\ displaystyle x \; = {\ overline {AC_ {1}}}, \; y = {\ overline {BC_ {2}}}}$${\ displaystyle z = {\ yliviiva {CA_ {2}}}}$

Seuraavat suhteet otetaan myös huomioon:

${\ displaystyle {\ overline {AI}} = {\ sqrt {r ^ {2} + s ^ {2}}}, \; \; \; {\ overline {BI}} = {\ sqrt {r ^ { 2} + t ^ {2}}}, \; \; \; {\ overline {CI}} = {\ sqrt {r ^ {2} + u ^ {2}}},}$

siinä termit tarkoittavat

${\ displaystyle s = {\ overline {AL_ {c}}}, \; t = {\ overline {BL_ {c}}}}$ ja ${\ displaystyle u = {\ overline {CL_ {a}}}.}$

Käytettyjen sopivien arvojen avulla on nyt mahdollista määrittää niin sanottu lisäosa${\ displaystyle {\ overline {PQ}}}$ , jonka pituus on${\ displaystyle m}$

${\ displaystyle m = {\ frac {1} {2}} \ vasen ({\ overline {AI}} + {\ overline {BI}} + {\ overline {CI}} - {\ overline {AL_ {c} }} - {\ overline {BL_ {c}}} - {\ overline {CL_ {a}}} + r \ oikea),}$

sovelletaan sitten edellä kuvattuihin tangenttiosiin

${\ displaystyle x = {\ overline {AC_ {1}}} = {\ overline {AI}} - m, \; \; \; y = {\ overline {BC_ {2}}} = {\ overline {BI }} - m, \; \; \; z = {\ overline {CA_ {2}}} = {\ overline {CI}} - m.}$

Määritetään erikseen summoille tekijän kaavassa${\ displaystyle m}$${\ displaystyle {\ frac {1} {2}}}$

${\ displaystyle m = {\ frac {1} {2}} {\ overline {AI}} + {\ frac {1} {2}} {\ overline {BI}} + {\ frac {1} {2} } {\ overline {CI}} - {\ frac {1} {2}} {\ overline {AL_ {c}}} - {\ frac {1} {2}} {\ overline {BL_ {c}}} - {\ frac {1} {2}} {\ overline {CL_ {a}}} + {\ frac {1} {2}} r,}$

hyvin yksinkertainen ja tilaa säästävä geometrinen rakenne (katso viereinen kuva) voidaan näyttää.

Malfatti piireissä Malfatti kanssa rakentamisen ylimääräisten reitin${\ displaystyle {\ overline {PQ}}}$

Rakenteen kuvaus

Piirtämisen jälkeen z. B. epätasainen kaksipuolinen kolmion kanssa puoli pituudet ja keskelle piirretyn ympyrän määritetään käyttämällä kolmea puolittajien ja . Tämä johtaa siihen, että linjat ja Seuraavassa on pudottamisen kohtisuorassa peräisin linjalle emäksen kanssa pisteen ja piirustus piirretyn ympyrän ympärillä kanssa säde laskeva on kohtisuorassa jopa pohjaan kohtaan ja jopa pohjaan kohtaan seuraavasti. ${\ displaystyle ABC}$ ${\ displaystyle a, \; b}$${\ displaystyle c}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$ ${\ displaystyle {\ overline {AI}}, {\ overline {BI}}}$${\ displaystyle {\ overline {CI}}.}$${\ displaystyle I}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle L_ {a}}$${\ displaystyle k}$${\ displaystyle I}$ ${\ displaystyle {\ overline {IL_ {a}}}.}$${\ displaystyle I}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle L_ {b}}$${\ displaystyle I}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle L_ {c}}$

Nyt pituus ylimääräinen reitti on määritettävä suoralle linjalle seuraavasti . Ensinnäkin radan puolikkaat ja lisätään radan puolikkaiden summasta ja vähennetään lopuksi ja saatu jäännöspuolisko Inkreisradius lisätään. ${\ displaystyle m}$${\ displaystyle {\ overline {PQ}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {AI}}, \; {\ frac {1} {2}} {\ overline {BI}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {CI}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {AL_ {c}}}, \; {\ frac {1} {2}} {\ overline {BL_ {c}}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {CL_ {a}}}}$${\ displaystyle {\ frac {1} {2}} r}$

Se jatkuu Malfatti-piireissä olevien keskusten määrittämisellä. Toisin sanoen, napauta apuosaa kompassilla ja siirrä se kolmelle puolittimelle ja kirjoitetun ympyrän keskeltä ; tämä johtaa siihen, että pisteiden ja pisteiden välillä, ja kaaren jopa kolmion ja kaaren asti ja mukaan lukien pisteiden ja seuraa pystyttämistä kolme pystysuoria alustasta pistettä ja asianomaisilla puolittaja ja siten haluttuja keskipisteiden ja tulos${\ displaystyle {\ overline {PQ}},}$${\ displaystyle m,}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle I}$${\ displaystyle D, \; E}$${\ displaystyle F.}$${\ displaystyle D}$${\ displaystyle E}$${\ displaystyle c}$${\ displaystyle F}$${\ displaystyle a}$${\ displaystyle C_ {1}, \; C_ {2}}$${\ displaystyle A_ {2}.}$${\ displaystyle C_ {1}, \; C_ {2}}$${\ displaystyle A_ {2}}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma};,}$${\ displaystyle M_ {A}, \; M_ {B}}$${\ displaystyle M_ {C}.}$

Saadaksesi yhteyspisteistä ja kolme plumb keikkuu on kaadettava keskustasta pisteiden ja päälle kolmion puolin ja uudelleen . Lopuksi piirrä Malfatti-ympyröihin ja säteillä ja saat heidän kolme viimeistä kosketuspistettä ja${\ displaystyle B_ {2}, \; A_ {1}}$${\ displaystyle B_ {1}}$${\ displaystyle M_ {A}, \; M_ {B}}$${\ displaystyle M_ {C}}$${\ displaystyle b, \; a}$${\ displaystyle b}$${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$${\ displaystyle r_ {A}, \; r_ {B}}$${\ displaystyle r_ {C}}$${\ displaystyle G, \; H}$${\ displaystyle J.}$

Siten kolme Malfatti-ympyrää ja niiden yhdeksän mahdollista kosketuspistettä on rakennettu. ${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$${\ displaystyle C_ {1}, \; C_ {2}, \; A_ {1}, \; A_ {2}, \; B_ {1}, \; B_ {2}, \; G, \; H }$${\ displaystyle J}$

Rakentaminen Steiner-Petersenin mukaan

Vuonna 1826 Jakob Steiner toi Malfatti-ympyrät kolmesta alakolmiosta muodostuvien ympyröiden yhteyteen, joita voidaan siksi käyttää Malfatti-ympyröiden rakennuselementtinä. Steiner muotoili seuraavan lauseen:

Tässä yhteydessä on korostettava, että Steinerin mainitsemat Malfatti-ympyröiden tangentit eivät yleensä ole puolittimia , vaan niiden peilikuvat suorilla viivoilla, jotka yhdistävät osittaisten kolmioiden kaksi ympyräkeskusta. ${\ displaystyle \ kolmio ABC}$

Vuonna 1879 Julius Petersen löysi alkeisgeometrisen ratkaisun (muunnelma ilman ennakkolaskelmia) Malfattin rakennusongelmaan, joka on esitetty alla.

Rakenteen kuvaus

Selkeyden vuoksi on edullista näyttää rakenne kolmessa päävaiheessa (1) - (3). Vain asiaankuuluvat rakenneosat siirretään ensimmäisestä vaiheeseen toiseen tai toisesta päävaiheeseen.

Malfatti kiertää Steiner-Petersenin mukaan
(1) Pääkohta: Osakolmioiden kolmen ympyrän rakentaminen ja${\ displaystyle \ kolmio BCI, \; \ triangle CAI}$${\ displaystyle \ kolmio ABI}$

(1) Osakolmioiden ja${\ displaystyle \ kolmio BCI, \; \ triangle CAI}$${\ displaystyle \ kolmio ABI.}$

Piirtämisen jälkeen z. B. epätasapuolinen kolmio , jonka sivupituudet ja kirjoitetun ympyrän keskipiste määritetään kolmella puolittimella ja . Inkreismittelpunkte ja osa-kolmiot ja saadaan jälleen leikkauksena kahden puolittajien, z. B. mukaan neljään osaan kulmat ja seuraa kaatuminen kohtisuoraan linjaan alustan kanssa pisteen ja piirustus piirretyn ympyrän ympärillä säteen kaato kohtisuorassa osoitteesta jopa pohjaan kohtaan ja jopa pohjaan kohtaan ja piirustus kahden viimeisen Ympyrät ja niiden keskipisteiden ympärillä tai ovat yhteydessä toisiinsa. ${\ displaystyle ABC}$${\ displaystyle a, \; b}$${\ displaystyle c}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle M_ {P}, \; M_ {Q}}$${\ displaystyle M_ {R}}$${\ displaystyle \ kolmio BCI, \; \ triangle CAI}$${\ displaystyle \ kolmio ABI}$${\ displaystyle \ alfa, \; \ beta,}$${\ displaystyle \ gamma.}$${\ displaystyle M_ {P}}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle P}$${\ displaystyle k_ {P}}$${\ displaystyle M_ {P}}$${\ displaystyle {\ overline {M_ {P} P}}.}$${\ displaystyle M_ {Q}}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle Q}$${\ displaystyle M_ {R}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle R}$${\ displaystyle k_ {Q}}$${\ displaystyle k_ {R},}$${\ displaystyle M_ {Q}}$${\ displaystyle M_ {R},}$

Malfatti kiertää Steiner-Petersenin
(2) päävaiheen mukaan: kolmen tangentin ja${\ displaystyle {\ overline {RZ}}, {\ overline {PX}}}$${\ displaystyle {\ overline {QY}}}$

(2) Kolmen tangentin ja${\ displaystyle {\ overline {RZ}}, {\ overline {PX}}}$${\ displaystyle {\ overline {QY}}}$

Se jatkuu liitoskohtia kanssa puolittaja radan vuonna ja piirros Thales ympyrä Hän leikkaa piirretyn ympyrän pisteissä ja nyt houkuttelee sinut ensimmäisen tangentti siitä kohdasta kautta pisteeseen, jossa piirretyn ympyrän kunnes ne saavuttavat kolmion vuonna leikkauksia. ${\ displaystyle R}$${\ displaystyle M_ {P},}$${\ displaystyle {\ overline {RM_ {P}}}}$${\ displaystyle M_ {1}}$ ${\ displaystyle k_ {1}.}$${\ displaystyle k_ {P}}$${\ displaystyle K}$${\ displaystyle L.}$${\ displaystyle R}$${\ displaystyle L}$${\ displaystyle k_ {P},}$${\ displaystyle b}$${\ displaystyle Z}$

Tämän jälkeen kanssa reitti kytkettynä on puolittunut ja laaksoon ympyrä sijaitsee. Hän leikkaa piirretyn ympyrän pisteissä ja piirtämisen toisen tangentti siitä kohdasta läpi , kunnes ne saavuttavat kolmion vuonna leikkauksia, toimittaa leikkauspiste Koska pisteen kolmantena tangentti on oltava, se vaatii sen määrittämistä vain rivi mukaan jopa kolmion sivu ja leikkauspiste, joten myös kolmas tangentti määritetään. ${\ displaystyle P}$${\ displaystyle M_ {Q}}$${\ displaystyle {\ overline {PM_ {Q}}}}$${\ displaystyle M_ {2}}$${\ displaystyle k_ {2}}$${\ displaystyle k_ {Q}}$${\ displaystyle O}$${\ displaystyle N.}$${\ displaystyle P}$${\ displaystyle N,}$${\ displaystyle b}$${\ displaystyle X}$${\ displaystyle T.}$${\ displaystyle T}$${\ displaystyle Q}$${\ displaystyle T}$${\ displaystyle c}$${\ displaystyle Y.}$${\ displaystyle {\ overline {QY}}}$

Malfatti-ympyrät Steiner-Petersenin
(3) päävaiheen mukaan: Malfatti-ympyröiden ja${\ displaystyle k_ {A}, k_ {B}}$${\ displaystyle k_ {C}}$

(3) Malfatti-ympyröiden ja${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$

Ensinnäkin puolittaja pisteestä puolittimeen piirretään kolmioon ; tämä johtaa ensimmäisen Malfatti-ympyrän keskelle . Tämän jälkeen pudottamalla kohtisuoraan päälle linjan kanssa emäksen pisteen ja vetämällä ensimmäinen Malfatti ympyrän ympäri säteen kanssa. Kaato kohtisuorassa jopa ja alustan kanssa pisteen ja tangentti alustaan kohta seuraavasti. Seuraava rivi alaspäin läpi puolittajan luo keskipiste. Kun toinen Malfatti ympyrä on piirretty sisään säteen kanssa , pystysuoria ovat leikattu ylös pohjan kanssa pisteen välillä ylös alustan kanssa pisteen ja on tangentti kanssa emäksen kohta . Seuraava rivi alas läpi puolittajan luo keskipiste. Nyt kolmatta Malfatti ympyrä on piirretty noin säteellä${\ displaystyle ARZ}$${\ displaystyle \ omega _ {\ epsilon}}$${\ displaystyle R}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle C_ {1}}$${\ displaystyle k_ {A}}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {M_ {A} C_ {1}}}.}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle B_ {2}}$${\ displaystyle M_ {A}}$${\ displaystyle RZ}$${\ displaystyle C '}$${\ displaystyle M_ {A}}$${\ displaystyle C '}$${\ displaystyle \ omega _ {\ beta}}$${\ displaystyle M_ {B}.}$${\ displaystyle k_ {B}}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {M_ {B} C '}}}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle C_ {2},}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle A_ {1}}$${\ displaystyle M_ {B}}$${\ displaystyle PX}$${\ displaystyle A '}$${\ displaystyle M_ {B}}$${\ displaystyle A '}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle M_ {C}.}$${\ displaystyle k_ {C}}$${\ displaystyle M_ {C}}$${\ displaystyle {\ overline {M_ {C} A '}}.}$

Pisteisiin kontakti ja saada, se silti vaatii kaksi juotteet saostetaan päässä on sekä päälle ja yhteys pisteen kanssa${\ displaystyle A_ {2}, \; B_ {1}}$${\ displaystyle B '}$${\ displaystyle M_ {C}}$${\ displaystyle {\ overline {BC}},}$${\ displaystyle M_ {C}}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {C}.}$

Siten kolme Malfatti-ympyrää ja niiden yhdeksän mahdollista kosketuspistettä on rakennettu. ${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$${\ displaystyle C_ {1}, \; C_ {2}, \; A_ {1}, \; A_ {2}, \; B_ {1}, \; B_ {2}, \; A ', \; B '}$${\ displaystyle C '}$

Rakentaminen Lobin ja Richmondin mukaan

Rakentaminen H.Lobin ja HW Richmondin mukaan,
tasasivuinen kolmio, johon on merkitty ympyrä osana maksimointiongelman ratkaisua

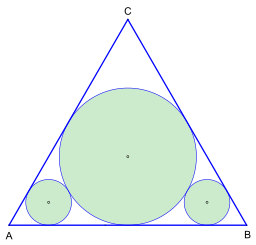
H. Lob ja HW Richmond julkaisivat ratkaisun Malfattin maksimointiongelmaan vuonna 1930. Tasasivuisen kolmion kaiverrettua ympyrää käytetään kolmen ympyränä. Kolmiomaisen alueen peitto tällä ympyröiden järjestelyllä on vain vähän suurempi, nimittäin , mutta tehtävä on helppo ja se voidaan esittää pienellä vaivalla. ${\ displaystyle \ noin 1 \, \%}$

Olet todistanut

Rakenteen kuvaus

Piirrettyään tasasivuisen kolmion, jonka sivut ovat yhtä pitkiä ja , kirjoitetun ympyrän keskipiste määritetään kolmella puolittimella ja . Tätä seuraa kohtisuoran putoaminen viivan kanssa peruspisteen kanssa ja piirretty ympyrä piirtäminen säteen ympärille , leikkauspisteet ovat puolittimen ja puolittimen kanssa . Kohtisuoran kaataminen ylöspäin peruspisteeseen ja ylöspäin peruspisteeseen seuraa . ${\ displaystyle ABC}$${\ displaystyle a, \; b}$${\ displaystyle c}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle I}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle D}$${\ displaystyle k}$${\ displaystyle I}$${\ displaystyle {\ overline {ID}};}$${\ displaystyle E}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle F}$${\ displaystyle \ omega _ {\ beta}.}$${\ displaystyle I}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle G}$${\ displaystyle I}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle H}$

Pienempien ympyrät piirtää kaksi kanssa samansuuntaisten (tasasivuisen kolmion)  - yksi piste jopa linjan kanssa risteys , toinen piste linjan kanssa risteyksessä perustaminen kohtisuoraan alustan päälle puolittaja ja kohtisuoran asettaminen puolittimelle peruspisteen kanssa johtaa keskipisteisiin ja nyt ympyrä piirretään ympäri säteellä ja ympyrä säteen kanssa . Kahden viimeisen kosketuspisteen saamiseksi kaadetaan sitten kaksi luumupalloa päältä ja sieltä , jolloin saadaan peruspisteet ja${\ displaystyle {\ overline {AB}}}$${\ displaystyle E}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle J}$${\ displaystyle F}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle K.}$${\ displaystyle J}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle \ omega _ {\ beta}}$${\ displaystyle K}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {B}.}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {M_ {A} E}}}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {M_ {B} F}}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {B}}$${\ displaystyle L}$${\ displaystyle M.}$

Siten kolme ympyrää ja niiden yhdeksän mahdollista kosketuspistettä on rakennettu tasasivuiseen kolmioon . ${\ displaystyle k, \; k_ {A}}$${\ displaystyle k_ {B}}$${\ displaystyle D, \; E, \; F, \; G, \; H, \; J, \; K, \; L}$${\ displaystyle M}$

Goldberg-rakennus

Michael Goldberg julkaisi vuonna 1967 esseen, jossa hän osoitti, että Malfatin rakenne kolmion muodosta riippumatta ei millään tavalla pysty täyttämään maksimointiongelmaa. Hän pääsi tähän tulokseen - todistamatta sitä - tutkimusten avulla käyttämällä kolmioiden eri muotoja, joilla kaikilla oli yksi yhteinen piirre: yksi kolmesta ympyrästä oli aina kaiverrettu ympyrä.

Rakenteen kuvaus

Rakennus Goldbergin mukaan, yleinen kolmio, johon on merkitty ympyrä yhtenä kolmesta ympyrästä, jotka ratkaisevat maksimointiongelman.
Säde tästä seuraa: Kolmas ympyrä on puolittimessa${\ displaystyle {\ overline {SR}} <{\ overline {OM}},}$${\ displaystyle \ omega _ {\ alpha}.}$

Kun olet piirtänyt epäsäännöllisen kolmion , merkityn ympyrän keskipiste määritetään käyttämällä kahta puolittajaa ja . Tämä johtaa siihen, että venytys ja seuraa saostuminen juotoksen etäisyyden ja jalka pisteeseen ja piirustus piirretyn ympyrän säde on risteyspistettä on tapauksessa, juotosten on päällä alustan kanssa kohta sekä siitä , että jalka kohta sisältää se . ${\ displaystyle ABC}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle {\ overline {AI}}}$${\ displaystyle {\ overline {CI}}.}$${\ displaystyle I}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle D}$${\ displaystyle I}$${\ displaystyle {\ overline {ID}};}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle E.}$${\ displaystyle I}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle F}$${\ displaystyle I}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle G}$

Toisen ympyrän keskipiste on nyt helppo määrittää kahdessa vaiheessa. On tarpeen vain kohtisuoraan polku pisteestä on leikkauksia, ja puolittaja kulman piste Näin valmistettu on keskellä toisen ympyrän säde ja yhteyspisteitä ja kaksi kolmion sivut. ${\ displaystyle {\ overline {AI}}}$${\ displaystyle E,}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle H}$${\ displaystyle AHE.}$${\ displaystyle J}$${\ displaystyle {\ overline {JE}}}$${\ displaystyle K}$${\ displaystyle L}$

Suurimman mahdollisen säteen löytämiseksi kolmannelle ja viimeiselle haetulle ympyrälle mahdolliset säteet määritetään ensin kahdesta puolikkaasta - kolmesta, jos kolmion muoto sitä vaatii. Se saadaan toistamalla analogisesti toisen ympyrän rakennusvaiheet keskipisteen kanssa.Viereisen kuvan katkoviivat esittävät puolittimelle rakennettua sädettä säteen vertailuna . Kahden säteen arviointi johtaa . Tästä seuraa: Keskuksen ympärillä oleva ympyrä on suurin mahdollinen kolmas ympyrä, jota haetaan. ${\ displaystyle J.}$${\ displaystyle \ omega _ {\ beta}}$${\ displaystyle {\ overline {SR}},}$${\ displaystyle {\ overline {OM}}}$${\ displaystyle \ omega _ {\ alpha}.}$${\ displaystyle {\ overline {SR}} <{\ overline {OM}}}$${\ displaystyle O}$

Rakentaminen Salgallerin ja Losin mukaan

WA Salgaller ja GA Los julkaisivat - vuoden 1992 todistustensa jälkeen (ks. Historia ) - vuonna 1994 Journal of Mathematical Sciences -lehdessä ratkaisunsa Malfatin maksimointiongelmaan. On u. a. kussakin voidaan nähdä viisi yleistä kolmiota, joista merkitty ympyrä on yksi kolmesta päällekkäisestä ympyrästä. Nämä kolme ympyrää makaavat samalla puolittimella vain sen kolmiossa, joka kuvataan Goldbergin mukaisessa rakenteessa .

Ilmainen käännös

Kolmiota peittää kolme ympyrää

• Malfatti-menetelmä (kuva 1) ja Steiner-Petersen-menetelmä saavutettiin

${\ displaystyle \ vasen ({\ sqrt {3}} - {\ frac {3} {2}} \ oikea) \ cdot \ pi \ noin 0 {,} 72910}$ tai noin ${\ displaystyle 72 {,} 91 \, \%.}$

• Lobin ja Richmondin (kuva 2) mukainen menetelmä saavutettiin

${\ displaystyle {\ frac {11 {\ sqrt {3}}} {81}} \ cdot \ pi \ noin 0 {,} 73895}$ tai noin ${\ displaystyle 73 {,} 90 \, \%.}$

• Menetelmä ympyrällä Salgallerin ja Losin mukaan sekä Goldbergin menetelmä (kuva 3 ja kuva 4):

Kolmion alueen peitto, esim. B. prosenttiarvona lähtökolmion valitusta muodosta sekä ympyröiden sijainnista ja riippuvaisista. Esitetyille muodoille ja vastaaville alueille sovelletaan prosenttikaavaa:${\ displaystyle k_ {2}}$${\ displaystyle k_ {3}}$${\ displaystyle A}$

${\ displaystyle {\ frac {A_ {k_ {1}} + A_ {k_ {2}} + A_ {k_ {3}}} {A {_ {\ kolmio {ABC}}}}} \ cdot 100 \, \%,}$

tämä johtaa kolmion pinta-alan peittämiseen kuvion 3 kolmiolle tai kuvion 4 kolmiolle${\ displaystyle \ noin 72 {,} 70 \; \%}$${\ displaystyle \ noin 77 {,} 1 \; \%.}$

• 

  Kuvio 1: Menetelmä, jonka Malfatti ja mukaisella menetelmällä Steiner-Petersen tasasivuisen kolmion, joka kattaa kolmikulmainen noin 72,91%

• 

  Kuva 2: Lobin ja Richmondin mukainen menetelmä tasasivuisessa kolmiossa, kolmion pinta-ala noin 73,90%

• 

  Kuva 3: Salgaller- ja Los-menetelmä sekä Goldbergin menetelmä merkityllä ympyrällä ; esitetyssä muodossa kolmion pinta-ala on noin 72,70% ${\ displaystyle k_ {1}}$

• 

  Kuva 4: Salgaller- ja Los-menetelmä sekä Goldbergin menetelmä merkityllä ympyrällä ; esitetyssä muodossa kolmion pinta-ala on noin 77,1% ${\ displaystyle k_ {1}}$

kirjallisuus

• Kurt Loeber: Osuudet Malfatti-ongelman ja sen laajennusten ratkaisuun ja historiaan. Perustutkielma. SUB Göttingen, Göttingen Digitalization Center, 1914, käyty 4. lokakuuta 2020 . 
• Marco Andreatta, Andras Bezdek, Jan P.Boronski: Malfatti-ongelma: kahden vuosisadan keskustelu , Mathematical Intelligencer, 2011, nro 1.
• Heinrich Dörrie : Malfattin ongelma 100 suuressa perusmatematiikan tehtävässä : niiden historia ja ratkaisut . Dover, New York 1965, ISBN 0-486-61348-8 , s. 147-151.
• Michael Goldberg: alkuperäisestä Malfatti Ongelma In Math. Mag. Nro 40, 1967, s. 241-247.
• Charles Stanley Ogilvy: Retket geometriassa . Dover, New York 1990, ISBN 0-486-26530-7 .
• WA Salgaller, GA Los: Malfattin ongelman ratkaisu . Julkaisussa: Journal of Mathematical Sciences . 72, nro 4, 1994, s. 3163-3177.

nettilinkit

• Eric W.Weisstein : Malfatti-ympyrät . Julkaisussa: MathWorld (englanti).
• Eric W.Weisstein : Malfattin ongelma . Julkaisussa: MathWorld (englanti).
• Malfattin ongelma. Julkaisussa: Cut The Knot. Haettu 4. lokakuuta 2020 . 

Yksittäiset todisteet

1. ↑ Kurt Loeber: Historiallinen katsaus (johdanto). Julkaisussa: Panokset Malfattin ongelman ja sen laajennusten ratkaisuun ja historiaan. SUB Göttingen, Götinger digitointikeskus, 1914, s. 1 , pääsee 15. marraskuuta 2020 . 
2. ^ Gianfrancesco Malfatti: Memoria sopra un problem stereotomica , Memorie di Matematica e Fisica della Società Italiana delle Scienze, No. 10, 1, 1803, s. 235–244, käytetty 15. marraskuuta 2020.
3. ^ Gianfrancesco Malfatti: Memoria sopra un problema stereotomica , Memorie di Matematica e Fisica della Società Italiana delle Scienze, No. 10, 1, 1803, s. 243, jäljempänä 15. marraskuuta 2020.
4. ↑ ^{a b} Ingmar Lehmann: 1. Malfatti-tarina, sivu 1. (PDF) julkaisussa: Malfatti-ongelma - aihe lahjakkaiden ihmisten mainostamisessa. TU Dortmund University, 2003, käyty 19. marraskuuta 2020 . 
5. ↑ ^{a b c d} Ingmar Lehmann: 1. Malfatti-tarina, sivu 2. (PDF) julkaisussa: Malfatti-ongelma - aihe lahjakkaiden opiskelijoiden edistämisessä. TU Dortmund University, 2003, käyty 7. marraskuuta 2020 . 
6. B ^{a b c d} Raúl Ibáñez: El problema de Malfatti. culturacientifica, Matemoción, 5. huhtikuuta 2017, käyty 5. lokakuuta 2018 (espanja). 
7. ↑ ^{a b c} Sic! - Mukaan transkriptio koskevan Saksan-Wikipediassa (alaviite 6) , tämä oikeinkirjoitus Los eroaa siitä oikeinkirjoitus Los' (jossa heittomerkki), joka on suurelta osin muualta , katso z. B. myös täällä.
8. ↑ ^{a b c d} Ingmar Lehmann: Malfatti-ympyröiden rakentaminen, s. 3–5. (PDF; 143 kt) Julkaisussa: Malfatti-ongelma - aihe lahjakkaiden mainostamisessa, 15 sivua. TU Dortmund University, 2003, käyty 4. lokakuuta 2020 . 
9. B ^{a b} Kurt Loeber: Historiallinen katsaus (johdanto). Julkaisussa: Panokset Malfattin ongelman ja sen laajennusten ratkaisuun ja historiaan. SUB Göttingen, Götinger Digitization Center, 1914, s. 2 ja sitä myöhemmin , Käytetty 4. lokakuuta 2020 . 
10. ^ Jacques Bernoulli: Oeuvres complètes, Geneve 1744, 1. osa, s.303.
11. ↑ Jakob Steiner: Joitakin geometrisia ehdotuksia ; Jacob Steinerin Gesammelte Werke, osa 1, G.Reimer, 1881, s.3, Google-teoshaulla, käytetty 15. marraskuuta 2020
12. ↑ Jakob Steiner: Joitakin geometrisiä näkökohtia ; Jacob Steinerin Gesammelte Werke, osa 1, G.Reimer, 1881, s.19, Google-teoshaulla, käytetty 15. marraskuuta 2020
13. ^ Alfred Clebsch: elliptisten toimintojen soveltaminen avaruuden geometrian ongelmaan. Julkaisussa: Journal for Pure and Applied Mathematics (Crelle's Journal), osa 53. SUB Göttingen, Götinger Digitization Center, 1857, s. 292–308 , käyty 15. marraskuuta 2020 . 
14. ^ Ajima Naonobu pääteoksessa Fukyo sampo vuodelta 1799. John J.O'Connor , Edmund F.Robertson :  Malfatti-ympyrä. Julkaisussa: MacTutor Mathematics History archive .
15. ^ ^{A b} H.Lob, HW Richmond: Malfattin kolmion ongelman ratkaisuista. (PDF) London Mathematical Society, 1930, käyty 20. marraskuuta 2020 . 
16. B ^{a b} Michael Goldberg: Alkuperäisestä Malfatti-ongelmasta . Julkaisussa: Florida Atlantic University (toim.): Mathematics Magazine . nauha 40 , ei. 5 , marraskuu 1967, s. 241-247 , JSTOR : 2688277 ( alkuperäisessä Malfatti Problem [PDF; näytetty 20 marraskuu 2020]). 
17. ↑ Ingmar Lehmann: Rakentaminen Steiner-Petersenin mukaan, sivu 5. (PDF) julkaisussa: Malfatti-ongelma - aihe lahjakkaiden opiskelijoiden mainostamisessa. TU Dortmund University, 2003, käyty 2. lokakuuta 2018 . 
18. ↑ Julius Petersen, R. von Fischer-Benzon (Überstzer): Menetelmät ja teoriat geometristen rakennusongelmien ratkaisemiseksi . Julkaisussa: Konstruktionsaufgabe 404. University of Michigan, Library, 1879, s.102-104 , käytetty 15. marraskuuta 2020 . 
19. ↑ ^{a b} Ingmar Lehmann: Rakentaminen Steiner-Petersenin mukaan, s. 8 ja sitä seuraavaa. (PDF) julkaisussa: Malfatti-ongelma - aihe lahjakkaiden opiskelijoiden edistämisessä. TU Dortmund University, 2003, käyty 2. lokakuuta 2018 . 
20. ↑ Sic! - Tämä Salgallerin oikeinkirjoitus vastaa Wikipediaa: nimeämiskäytännöt , katso myös Wiktor Abramowitsch Salgaller
21. ↑ ^b W. A. Salgailer, GA Los: ratkaisu Malfatti ongelma . Julkaisussa: Journal of Mathematical Sciences . 72, nro 4, 1994, s.  3163 ja sitä seuraavat, kuva 1, Springer Link, PDF . Haettu 5. lokakuuta 2020.
22. Ime Jaime Rangel-Mondragon: Malfatti-ongelma. (PDF) julkaisussa: Wolfram Demonstrations Project. Wolfram, 2011, käyty 24. marraskuuta 2020 . 
23. ^ Arnold Math Jn: 2.2 Ratkaisu Malfattin marmoriongelmaan. (PDF) julkaisussa: Malfattin marmoriongelmasta. Matemaattisten tieteiden instituutti, Stony Brook University, New York, kesäkuu 2016, käyty 24. marraskuuta 2020 . 

Tämä artikkeli on lisätty luetteloon erinomaisia artikkeleita on tässä versiossa 25. marraskuuta 2020 .