Tämän artikkelin otsikko on epäselvä. Muut merkitykset on lueteltu kohdassa
Tensori (täsmennys) .
Tensor on usean muuttujan kartoitus , joka kartoittaa tietyn määrän vektoreita vektorin pinnalle, ja joka täyttää yleinen ominaisuus . Se on matemaattinen objekti lineaarisesta algebrasta , jota käytetään monilla alueilla, mukaan lukien differentiaaligeometria , ja joka laajentaa lineaarisen kartoituksen käsitettä . Termi otettiin alun perin käyttöön fysiikassa ja vasta myöhemmin sitä täsmennettiin matemaattisesti.
Differentiaaligeometriassa ja fyysisissä tieteenaloissa ei yleensä oteta huomioon lineaarisen algebran mukaisia tentereitä, vaan käsitellään pikemminkin tensorikenttiä , joita yksinkertaisuuden vuoksi usein kutsutaan myös tentoreiksi. Tensorikenttä on kartta, joka määrittää tensorin jokaiseen avaruuden pisteeseen. Monet fyysisen kentän teoriat käsittelevät tensorikenttiä. Näkyvin esimerkki on yleinen suhteellisuusteoria . Tensorikenttien tutkimista käsittelevää matemaattista osa-aluetta kutsutaan tensori-analyysiksi, ja se on tärkeä työkalu fysiikan ja tekniikan aloilla.
Käsitteen historia
Sana tensori (johdettu latinalaisesta tarjouksesta `` span '' ), otettiin matematiikkaan 1840 -luvulla William Rowan Hamiltonin toimesta ; hän käytti sitä ilmaistakseen kvaternioidensa absoluuttisen arvon , eli ei tensori nykyaikaisessa mielessä. James Clerk Maxwell ei näytä kutsuneet jännitystensoria , jonka hän siirtyi kimmoteoria ja electrodynamics itsekin.
Nykyaikaisessa merkityksessään, skalaarin , vektorin ja matriisin yleistyksenä , sanan tensori esitteli ensimmäisen kerran Woldemar Voigt kirjassaan Kristallien perusfysikaaliset ominaisuudet alkeellisessa esityksessä (Leipzig, 1898).
Otsikolla absoluuttinen differentiaaligeometria , Gregorio Ricci-Curbastro ja hänen oppilaansa Tullio Levi-Civita kehittivät tensorilaskennan Riemannin jakotukkeihin noin vuonna 1890 . He antoivat tuloksensa laajemman asiantuntijayleisön saataville vuonna 1900 kirjalla Calcolo differenziale assoluto , joka käännettiin pian muille kielille ja josta Albert Einstein hankki matemaattiset perusteet, joita hän tarvitsi yleisen suhteellisuusteorian muodostamiseen . Einstein itse keksi termin tensori -analyysi vuonna 1916 ja auttoi teoriansa myötä merkittävästi tensorilaskennan popularisointiin; Lisäksi hän esitteli Einsteinin summakäytännön , jonka mukaan kaksoisindeksit lisätään ja summasymbolit jätetään pois.
Tenorityypit
Äärellisestä ulottuvuudesta vektoriavaruudesta alkaen skalaareja kutsutaan tyyppitensoreiksi , sarakevektoreita tyyppitensoreiksi ja covectors (tai rivivektoreita) tyyppitensoreiksi . Ylemmän tason tenorit määritellään monirivisiksi yhdistämisiksi ja alemman tason tenorit argumentteiksi ja kartta -arvoiksi. Esimerkiksi tyypin tensori voidaan ymmärtää lineaarisena kartoituksena vektoriavaruuksien välillä tai bilineaarisena kartoituksena, jossa on vektori ja peitin argumentteina.




Esimerkiksi fysiikan mekaaninen jännitystensori on toisen asteen tensori - luku ( jännityksen voimakkuus ) tai vektori ( tärkein jännityssuunta ) eivät aina riitä kuvaamaan kehon jännitystilaa . Sitä pidetään tyypin tensorina , se on lineaarinen kartoitus, joka määrittää siihen vaikuttavan voiman (peittimenä) pintaelementille (vektoriksi), tai bilineaarinen kartoitus, joka osoittaa työn, joka tapahtuu siirtymän aikana Pintaelementti pintaelementtiin ja siirtymävektoriin vaikuttavan jännitteen vaikutus suoritetaan.

Kiinteän vektoriavaruuden perusteella saadaan seuraavat esitykset erityyppisistä tentoreista:
- Skaalaari yhdellä numerolla
- Yksi vektori yhdellä sarakevektorilla
- Viivavektorin rinnakkaisvektori
- Toisen asteen tensori matriisin läpi
Jännitystensorin käyttö pintaelementtiin on tällöin z. B. annettu pylväsvektorin sisältävän matriisin tulolla. Korkeamman asteen tentoreiden koordinaatit voidaan järjestää vastaavasti korkeamman ulottuvuuden kaavioon. Toisin kuin sarakevektori tai matriisi, näillä tensorin komponenteilla voi olla enemmän kuin yksi tai kaksi indeksiä. Esimerkki kolmannen kertaluvun tensorista, jonka argumentteina on kolme vektoria des , on 3 × 3 -matriisin determinantti kyseisen matriisin sarakkeiden funktiona. Mitä tulee ortonormaaliin , sitä edustaa Levi-Civita-symboli .


Vektoreiden rinnakkais- ja ristiriitaisuus
Termit co- ja contravariant viittaavat vektoreiden, lineaaristen muotojen koordinaattien esitykseen , ja kuten jäljempänä artikkelissa kuvataan, niitä sovelletaan myös tentoreihin. Ne kuvaavat, miten tällaiset koordinaattiesitykset käyttäytyvät perusmuutoksen taustalla olevan vektoriavaruuden suhteen.
Jos määritellään perusta -ulotteisessa vektoriavaruudessa , tämän avaruuden jokainen vektori voidaan esittää numerotyypillä - sen koordinaateilla - käyttäen . Jos koordinaattien esitys perustuu eri kantaan , koordinaatit (yksi ja sama vektori) muuttuvat suhteessa uuteen tukikohtaan. Siirtyminen toiseen perustaan edellyttää siksi koordinaattien esityksen muuttamista. Seuraava pätee: Jos uusi perusta määritetään vanhan kannan perusteella, uudet koordinaatit saadaan vertaamalla









niin:

Jos esimerkiksi pyöritetään ortogonaalista kantaa kolmiulotteisessa euklidisessa avaruudessa -akselin ympärillä , koordinaattivälin koordinaattivektorit pyörivät myös -akselin ympäri , mutta vastakkaiseen suuntaan eli ympäri . Tätä perusmuunnosta vastakkaista muutoskäyttäytymistä kutsutaan vastakkaiseksi . Usein merkinnän lyhentämiseen käytettävät vektorit identifioidaan niiden koordinaattivektoreiden kanssa, joten vektoreihin viitataan yleensä vastavariantteina.






Toisaalta lineaarinen muoto tai covector on skalaariarvoinen lineaarinen kartoitus vektoriavaruudesta. Voit määrittää sen koordinaateiksi sen arvoilla perusvektoreiden ,, perusteella . Lineaarisen muodon koordinaattivektorit muuttuvat kuten perusnumero kuten




siksi tätä muutoskäyttäytymistä kutsutaan kovarianssiksi . Jos taas tunnistetaan lineaariset muodot koordinaattivektoreineen, myös lineaariset muodot määritetään yleensä kovarianteiksi. Kuten vektoreiden kohdalla, taustalla oleva perusta ilmenee kontekstista. Tässä yhteydessä puhutaan myös kaksoisvektoreista.
Nämä nimet siirretään tenoreille. Tämä selitetään seuraavassa osassa, joka koskee tensoijien määritelmää .

määritelmä
( r , s ) -anturitila
Seuraavassa kaikki vektoriavaruudet ovat rajallisia ruumiin päällä . Kanssa puhelun asetettu kaikkien lineaaristen muotojen päässä vektori tila on runko ja - yleisemmin - kanssa asetettu kaikkien -linear kuvat on -Vektorraums on vektoriavaruudessa . Ovatko vektoreiden välilyönnit ohi , vektori-avaruus, jossa on useita lineaarisia muotoja, joilla on nimetty. Vastaavasti tarkoittavat asetettu kaikkien - Multilineaarinen kuvaukset , tässä erityisesti kertaiseksi -linear kuvaukset. Kun kyseessä on ja The muodot ovat bilineaari .






















Jos - vektoriavaruuteen kutsutaan sen duaaliavaruus . Sitten on olemassa (mukaan yleispalvelun omaisuus ) kanoninen isomorfisuudella



ja yleisemmin

Kanoninen isomorphism on vektorin tilan , jossa sen kaksi tilaa seuraavasti (korvaamalla mukaan ja näin ollen mukaan ), joka on isomorfinen , että tensoritulo . (Toteutumiseksi tensoritulo tila tilana usean muuttujan muotoja sekä kanoninen tunnistamiseen , jota käytetään useammin tässä osassa, katso osiot yleistä omaisuutta ja tensor tuotteiden ja usean muuttujan muodot .)










On olemassa seuraavanlaisia luonnollisia isomorfismeja :

Nämä luonnolliset isomorfisuudella perustuvat vähentämiseen kertainen-lineaarikuvausten ja kertainen-lineaarikuvausten (ks currying tai Schönfinkeln ) toisaalta ja yleinen ominaisuus tensoritulo toisaalta - levitetään useita kertoja:



Edellä esitetty luonnollinen isomorfismi on olemassa
erityisesti
![{\ displaystyle {\ begin {matrix} L ^ {k} (E_ {1}, \ dotsc, E_ {k}; K) & {\ stackrel {\ sim} {\ longrightarrow}} & L (E_ {1} \ otimes \ dotsc \ otimes E_ {m}; E_ {m + 1} ^ {*} \ otimes \ dotsc \ otimes E_ {k} ^ {*}) \\\ lambda & \ longmapsto & \ left [\ lambda _ {(1, \ piste, m)} \ kaksoispiste v_ {1} \ otimes \ dotsc \ otimes v_ {m} \ mapsto \ lambda _ {(v_ {1}, \ piste, v_ {m})} \ in ( E_ {m + 1} \ otimes \ dotsc \ otimes E_ {k}) ^ {*} \ right] {\ text {,}} \\ && {\ text {where}} \ vasen [\ lambda _ {(v_ {1}, \ dotsc, v_ {m})} \ kaksoispiste (v_ {m + 1} \ otimes \ dotsc \ otimes v_ {k}) \ mapsto \ lambda (v_ {1}, \ piste, v_ {k} ) \ oikea] \\\ loppu {matriisi}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5af0ca5982fcea7f59fe2aa8996dd0c3de44ce0)
ja tunnistus tehdään lineaariselle lomakkeelle . Tässä yhteydessä riittää, jotta määritellä kartoitukset on
ala-tensors (katso myös kohta Tensor osana tensoritulo ) kuin tuottavan järjestelmän yli perusrungon . On lisättävä, että tapauksissa ja tyhjä tensorituote syntyy, joka voidaan tunnistaa peruskappaleesta . Erityisesti on siis kyse vektorivälistä ja tunnistamisesta









-
 .
.
Määritelmä: Jos kiinteä vektoriavaruus yli kehon dual tilaa Antaa määritellään





jossa merkinnät ja merkinnät . Tämän sarjan elementtejä kutsutaan
tentoreiksi, tason vastaisiksi ja tason kovarianteiksi . Lyhyesti sanottuna puhutaan tyyppitensoreista . Summa on nimeltään taso tai sijoitus tensor.







Edellä esitettyjen näkökohtien (varten ja sekä varten ja varten ) kokonaistulos on







Joten vektori tila on tensors tyyppiä toteuttaa
tensoritulo , nimittäin kautta edellä kanoninen tunnistaminen



-
 .
.
Nämä luonnolliset isomorfisuudella tarkoittaa, että yksi voi myös
induktiivisesti määritellä kiristimet tason kuin usean muuttujan kuvaukset välillä tensor tilojen alemman tason. Tietyn tyyppiselle tensorille on useita vastaavia mahdollisuuksia.

Fysiikassa vektorivälit eivät yleensä ole identtisiä, esim. B. nopeus- ja voimavektoria ei voi lisätä. Ohjeita voidaan kuitenkin verrata keskenään, ts. Toisin sanoen tunnistetaan vektorivälit keskenään
skalaaritekijää lukuun ottamatta . Näin ollen tyyppisten tenorien määritelmää voidaan soveltaa vastaavasti. On myös mainittava, että (ulottuvuus) skalaarit fysiikassa ovat yksiulotteisten vektoritilojen elementtejä ja että skalaarituotteella varustetut vektoriavaruudet voidaan tunnistaa niiden kaksoisavaruudesta. Yksi toimii z. B. voimavektoreilla, vaikka voimat ilman skalaarituotetta on katsottava kovektoriksi.

Ulkoinen tensorituote
An (ulompi) tensoritulo tai
tensor kertolasku on yhteys kahden tensors. Antaa olla vektori tilaa ja olla ja tensors. (Lähtö) tensorituote ja on tensori, joka on kulkenut läpi








on määritelty. Tässä niitä ja niitä .


Esimerkkejä ( r , s ) -antureista
Anna ja ole äärellisulotteiset vektoriavaruudet seuraavassa.


- (0,0) -anturien sarja on isomorfinen alla olevan rungon kanssa . Et liitä runkoelementtiä mihinkään lineaariseen muotoon tai vektoriin. Siksi nimitys (0,0) -antureiksi.

- (0,1) -tensors järjestää mikä tahansa lineaarinen muoto, ja vektorin joukko, mikä vastaa lineaarisen muotoja on .


- (1,0) Tensors määrittää numeron lineaariseen muotoon eikä vektoriin. Ne ovat siis kaksivaiheisen vektoriavaruuden elementtejä . Äärellisten ulottuvuuksien vektoriavaruuksien tapauksessa ne vastaavat alkuperäisiä vektoriavaruuksia , koska seuraava pätee tässä (katso isomorfismi ).



- Lineaarinen kartoitus välillä finite-ulotteinen vektori tilat voidaan ymmärtää osana ja on sitten (1,1) -tensor.


- Bilineaarinen muoto voidaan ymmärtää osana, toisin sanoen kuten (0,2) -tensor. Erityisesti skalaarituotteet voidaan ymmärtää (0,2) tentoreina.


- Kroneckerin delta on taas (0,2) tensor. Se on osa ja siksi monirivinen kartoitus . Moniriviset kartoitukset määräytyvät ainutlaatuisesti perusvektorien vaikutuksen perusteella. Joten Kronecker Delta on selvästi läpi




- varmasti.
- Determinantti on matriisien, tulkitaan vuorotellen usean muuttujan muodossa sarakkeet, on (0, n) -tensor. Mitä tulee ortonormaaliin, sitä edustaa Levi-Civita-symboli ("epsilon-tensori"). Erityisesti kolmessa todellisessa ulottuvuudessa determinantti on kolmannen kertaluvun tensori ja se koskee ortonormaalin perustan elementtejä. Sekä Kronecker-deltaa että Levi-Civita-symbolia käytetään laajalti tenssien symmetriaominaisuuksien tutkimiseen. Kroneckerin delta on symmetrinen, kun indeksit vaihdetaan, Levi-Civita-symboli on epäsymmetrinen, joten tenorit voidaan jakaa niiden avulla symmetrisiksi ja epäsymmetrisiksi osiksi.



- Toinen esimerkki toisen asteen kovarianssitensorista on hitaustensori .
- Kun kimmoisuusteorian , yksi yleistää Hooken yhtälö välisestä suhteesta voimien ja liittyvät kannat ja vääristymät elastisen väliaineessa, myös avulla tensor hammaskiven tuomalla kanta tensor , jossa kuvataan vääristymiä ja muodonmuutokset, ja jännitystensoria , joka kuvaa muodonmuutoksia aiheuttavia voimia. Katso myös jatkumekaniikka .
- Antaa olla vektoriavaruus skalaarituotteen kanssa . Kuten edellä mainittiin, skalaaritulo on lineaarinen molemmissa väitteissä, eli (0,2) -tensori tai kaksinkertainen kovarianssitensori. Puhutaan myös metrisestä tensorista tai lyhyesti sanottuna "metristä". Tässä on huomattava, että se itsessään ei ole metrinen tila , vaan luo sen. Metriikan koordinaatit suhteessa vektoriavaruuteen on merkitty; ja olkoon vektoreiden koordinaatit ja suhteessa samaan pohjaan. Siksi seuraava koskee kahden vektorin kartoittamista ja metrisen alapuolella














- Siirtyminen rinnakkaisten ja vastaisten tentoreiden välillä voidaan suorittaa metrisen avulla

- suorittaa.
- Riemannin jakotukien differentiaaligeometriassa tämä mittari on myös sijainnin funktio. Paikan tensori-arvoista funktiota kutsutaan tensorikentäksi , metrisen tensorin tapauksessa nimenomaan Riemannin metriksi.
Pohja
Perusta ja ulottuvuus
Antaa olla vektoriavaruus kuten yllä, niin välilyönnit ovat myös vektoriavaruuksia. Lisäksi olkoon nyt rajallinen ulottuvuus alustan kanssa . Kaksoisperustaa merkitään. Tenorien tila on tällöin myös äärellinen ja







on tämän tilan perusta. Tämä tarkoittaa, että jokainen elementti voi käydä läpi


olla edustettuna. Tämän vektoriavaruuden ulottuvuus on . Kuten jokaisessa äärellisulotteisessa vektoriavaruudessa, myös tensointiavaruudessa riittää, kun sanotaan, miten funktio toimii sen perusteella.

Koska yllä oleva summanäyttö sisältää paljon paperityötä, käytetään usein Einsteinin summakäytäntöä . Joten tässä tapauksessa kirjoitat

Kertoimia kutsutaan tensorin osiksi pohjaan nähden . Usein tensorin osat tunnistetaan tensorin kanssa. Katso tästä fysiikan tensoriesitykset .


Perusmuutos ja koordinaattimuutos
Antaa ja olla pareja vektoriavaruuksien eri kannoista . Jokainen vektori, mukaan lukien kaikki perusvektorit, voidaan esittää perusvektoreiden lineaarisena yhdistelmänä . Perusvektoria edustaa







Koot määrittävät emäksen muunnoksen emästen ja . Se koskee kaikkia . Tätä prosessia kutsutaan perustan vaihtamiseksi .




Anna myös tensorin osien olla pohjaan nähden . Yhtälö johtaa sitten tensorikomponenttien muunnoskäyttäytymiseen




Pääsääntöisesti erotetaan tensorin ja transformaatiomatriisin koordinaattiesitys . Muunnosmatriisi on indeksoitu määrä, mutta ei tensori. Euklidisessa avaruudessa nämä ovat kiertomatriiseja ja erikois suhteellisuusteoriassa z. B. Lorentzin muunnokset , jotka voidaan ymmärtää myös "kiertoina" nelidimensionaalisessa Minkowskin avaruudessa . Tässä tapauksessa puhutaan nelitensoreista ja nelivektoreista .



esimerkki
Komponenttien avulla tensori voidaan esittää suhteessa pohjaan. Esimerkiksi tensori, jolla on sijoitus 2 tietyssä perusjärjestelmässä, voidaan esittää matriisina seuraavasti:



Tämä mahdollistaa arvon laskemisen vastaavan perusjärjestelmän puitteissa matriisin kertomisen avulla :


Jos nyt tarkastellaan erityisesti hitaus tensoria , sitä voidaan käyttää jäykän kappaleen pyörimisenergian laskemiseen kulmanopeudella suhteessa valittuun koordinaattijärjestelmään seuraavasti:




Toiminta tentereillä
Tensorituotteen lisäksi (r, s) -antureille on muita tärkeitä toimintoja.
Sisäinen tuote
Tensorin sisältävän vektorin (tai (rinnakkain) vektorin ) sisäinen tuote on (tai ) -tensori, joka






tai läpi

on määritelty. Tämä tarkoittaa, että tensori arvioidaan kiinteällä vektorilla tai kiinteällä kovektorilla .




Tensorikartio
Annetut ovat (r, s) -tensori ja ja . Tensorin kartio muodostaa tensorin




tensorin päällä

pois. Tätä prosessia kutsutaan tensorin kapenevaksi tai radanmuodostukseksi. (1,1) tentureiden tapauksessa tensorin kartio vastaa

tunnistetaan jälkeäkään endomorphism.

Einsteinin summauskäytännön avulla tensorikartio voidaan esittää hyvin lyhyesti. Olkoon esimerkiksi kaksivaiheisen tensorin kertoimet (tai koordinaatit) suhteessa valittuun perustaan. Jos tätä (1,1) -tensoria halutaan pienentää, kirjoitetaan usein vain kertoimien sijasta . Einsteinin yhteenvetokäytännössä todetaan nyt, että kaikki samat indeksit lasketaan yhteen ja on siten skalaari, joka vastaa endomorfismin jälkiä. Ilmaisua sitä vastoin ei ole määritelty, koska samat indeksit lasketaan yhteen vain, jos yksi on ylhäällä ja toinen alhaalla. Toisaalta se on ensimmäisen asteen tensori.







Takaisinveto (paluukuljetus)
Antaa olla lineaarinen kartoitus vektorivälien välillä, joiden ei tarvitse olla isomorfismi. Paluu on luku, joka menee läpi




on määritelty. On ja .


Työnnä eteenpäin
Antaa olla vektori avaruuden isomorfismi . Määrittele työntää eteenpäin läpi kanssa




On , ja . Kanssa tahdon paluukuljetus lineaarisen muodon luettelossa. Konkreettisesti tämä tarkoittaa analogista paluukuljetusta, voidaan luopua työntövoiman isomorfismista ja määritellä tämä toiminto vain tentoreille.








Tensorialgebra
Antaa olla vektoriavaruus yli ruumiin . Sitten se on ohi



määrittelee ns. tensorialgebran. Tensorituotteen homogeenisten komponenttien kertomalla siitä tulee yhtenäinen assosiatiivinen algebra .

Tensorin tuotetila
Tässä osassa määritellään tensorituotetilat; niitä käsitellään tyypillisesti algebrassa . Tämä määritelmä on yleisempi kuin (r, s) -anturit, koska täällä tensoritiloja voidaan rakentaa eri vektoritiloista.
Yleinen ominaisuus kahden tekijän tensorituotteelle
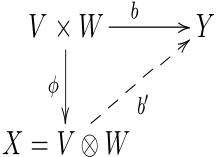
Tensorituotteen yleinen ominaisuus
Anna ja vektori välilyöntejä kentän päälle . Jos on olemassa muita vektoriavaruuksia, kaikki bilineaarinen kartoitus ja lineaarinen kartoitus, niin linkki on myös bilineaarinen kartoitus. Jos annetaan bilineaarinen kartoitus, siitä voidaan rakentaa mikä tahansa määrä muita bilineaarisia karttoja. Herää kysymys, onko olemassa bilineaarinen kartoitus, josta kaikki bilineaariset kartat voidaan rakentaa tällä tavalla (yksiselitteisellä tavalla) yhdistämällä ne lineaarisiin karttoihin . Tällainen universaali kohde, ts. H. bilineaarista kartoitusta, mukaan lukien sen kuva -alue, kutsutaan tensorituotteeksi ja .











Määritelmä: Kuten vektoriavaruuksien ja kunkin vektoriavaruuden tensorituotetta kutsutaan, jolle on olemassa bilineaarinen kartoitus, joka täyttää seuraavan yleisominaisuuden :





- Jokaista bilineaarinen kartoitus ja vektoriin tila on täsmälleen yksi lineaarinen kartoitus siten, että sovelletaan kaikkiin :






Jos tällainen vektoriavaruus on olemassa , se määritetään ainutlaatuisesti isomorfismia lukuun ottamatta . Jos on jo toinen tällainen vektoriavaruus, jossa on bilineaarinen muoto (sen tensorituotteena ) , silloin ominaisuuden kanssa yksilöllisesti määritetyn lineaarisen kartoituksen lisäksi on myös yksilöllisesti määritetty lineaarinen kartoitus ominaisuuden kanssa , koska sillä on myös yleisominaisuus. Joten molemmat ja ovat isomorfismeja. Yksi kirjoittaa ja . Joten yleisominaisuus voidaan kirjoittaa muodossa. Tällaisten tuotetilojen rakentamisessa viitataan artikkeliin Tensor -tuote .















Tensorituotteen yleinen ominaisuus antaa myöntävän vastauksen yllä olevaan kysymykseen ja voidaan muotoilla seuraavasti: Kartoitus

on surjektiivinen (olemassaolon toteamus) ja injektiivinen (ainutlaatuisuuden toteamus), siksi bijektiivinen ja siten vektoritilojen isomorfismi. Tässä tapauksessa tensorituotetilan kaksoistila tulkitaan bilineaaristen muotojen avaruudeksi. Yhdessä jo mainittujen tunnisteiden kanssa tämä johtaa:

Tensori osana tensorituotetta
Matematiikassa tenorit ovat tensorituotteiden elementtejä.
Olkoon se elin ja on vektoriavaruuksia ruumiin yläpuolelle .



Tensoritulo of on vektori tila, jonka elementit ovat summia symbolien muodossa




ovat. Näitä symboleja koskevat seuraavat laskentasäännöt:


Lomakkeen tentoreita kutsutaan alkeisiksi. Jokainen tensoija voidaan kirjoittaa alkeis tenorien summana, mutta tämä esitys ei ole yksiselitteinen paitsi triviaaleissa tapauksissa, kuten voidaan nähdä ensimmäisestä laskentasäännöstä.

Jos on perusta on (varten , ), niin on





mitan perusta on siksi yksittäisten vektoritilojen mittojen tulo


Laajennus useisiin tekijöihin: Yleinen ominaisuus useille tensorituotteille ja monirivisille muodoille
Edellisen näkökohdat on universaali ominaisuus voidaan laajentaa useisiin tekijöihin seuraavasti.
Duaaliavaruus on tölkin (mukaan yleinen ominaisuus), voidaan tunnistaa tilan kanssa on - usean muuttujan muodoissa :



- Jos lineaarinen muoto on päällä, niin - antaa Multilineaarinen muodossa . Herää kysymys, voidaanko jokainen monilinjainen muoto muodostaa tällä tavalla. Myönteiset vastauksesta saa universaali ominaisuus tensoritulo:





- Kääntäen , jos -Multilinearform on, sitten lineaarinen lomakkeelle se - mukainen yleinen ominaisuus - on määritetään määrittelemällä se, että ala-tensors (mukaisesti yleinen ominaisuus) ja sitten laajentamalla sitä lineaarisesti koko vektorin tilaa . Yleisominaisuuden mukaan perustekijöihin sovelletaan seuraavaa:





Kuten edellä (yleisominaisuutta koskevassa osassa) on muotoiltu kahden vektoriavaruuden tapauksessa, yleisominaisuus koskee myös useita tekijöitä (paitsi isomorfismi). Ja tämä voidaan muotoilla seuraavalla tavalla ja sisältää samanaikaisesti kahden yllä olevan peilipisteen lausuman:
Määritelmä: Olkoon sekä ja että vektorivälit kehon yläpuolella . Sitten monen lineaarikuvauksen kutsutaan tensoritulo vektorin tilojen yli , jos se on seuraava ominaisuus: sellaisten usean lineaarinen kuvantaminen , on olemassa ainutlaatuinen lineaarinen kartta kiinteistön kaikkien tuplat sitten kirjoittaa:












Jos on olemassa sellainen vektoriavaruus, jolla on tällainen monirivinen kartoitus , vektoriavaruus määritetään yksilöllisesti lukuun ottamatta isomorfismia tämän yleisominaisuuden vuoksi. Siksi puhumme usein vain vektoriavaruudesta , vaikka tarkkaan ottaen siihen liittyvä monirivinen kartoitus on myös osa tensorituotetta.




Itse asiassa tällainen tensorituote voidaan rakentaa vektoriavaruuksien luokalle (tarkemmin sanottuna: monirivisten kartoitusten kategoriassa annetuilla vektoriavaruuksilla mihin tahansa vektoritilaan) . Sille on selvästi ominaista sen yleismaailmallinen ominaisuus isomorfismia lukuun ottamatta.
![{\ displaystyle \ psi: V_ {1} \ kertaa \ pistettä \ kertaa V_ {s} \ - [??]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/597d0dd2574ad69e6b77499917be8e727960cd06)

Joten jos tensoritulo (isomorfismia lukuun ottamatta) merkitsee vektoriavaruuksien tensorituloa , universaali ominaisuus muodostaa vektoriavaruuksien isomorfismin (huomaa: lineaaristen kuvausten tila ja monirivisten kuvausten tila ovat luonnollisesti vektorivälit):



Tämän kartoituksen surjektiivisuus on synonyymi olemassaololausekkeelle ("on olemassa jokaiselle moniriviselle kartoitukselle", vrt. Toinen peilipiste), kun taas injektiokyky vastaa ainutlaatuisuuslausetta ("selvästi määritetty"). Koska annettu kartoitus on lineaarinen kartoitus (vektoritilojen homomorfismi), se on vektoriavaruuksien isomorfismi.
Jos kaikki tarkasteltavat vektoriavaruudet ovat äärellisulotteisia, voidaan tapaukselle käyttää kahta vektoriavaruutta


samaistua toisiinsa luonnollisesti, d. eli vastaavien monilinjaisten muotojen elementtejä


Muuttujat tenoreista 1 ja 2
Invariants yksi- tai kaksivaiheinen tensor ovat skalaareja, jotka eivät muutu ortogonaalisia koordinaattimunnosten tensor. Ensimmäisen asteen tentoreille skalaarituotteen indusoiman normin muodostuminen johtaa invarianttiin
-
 ,
,
Tässä ja seuraavassa käytetään jälleen Einsteinin yhteenvetokäytäntöä. Toisen asteen tenoreille kolmiulotteisessa euklidisessa avaruudessa voidaan yleensä löytää kuusi pelkistymätöntä invarianttia (ts. Invariantteja, joita muut invariantit eivät voi ilmaista):

Symmetristen toisen asteen tentoreiden (esim. Venytystensori ) tapauksessa invariantit ja samat. Lisäksi kolme muuta invarianttia voidaan esittää (joten se ei ole enää pelkistymätön). Determinantti on myös riippumaton; se voidaan esittää, esimerkiksi matriisien yli supistumattoman invariantit , ja kuten







Sillä antisymmetrisiä tensors koskee , , ja voidaan taas katsoa. Siten kolmiulotteisessa euklidisessa avaruudessa toisen tason symmetrisillä tentoreilla on kolme redusoitumatonta invarianttia ja toisen tason antisymmetrisillä tentoreilla yksi redusoitumaton invariantti.





Vektoriavaruuden ja symmetrian tensorituotteet
Vektoriavaruuden tensorituotteen voi muodostaa itsensä kanssa. Ilman vektoriavaruuden tuntemusta voidaan määritellä tensorituotteen automorfismi , joka koostuu puhtaiden tuotteiden tekijöiden vaihtamisesta:




Koska tämän kartoituksen neliö on identiteetti, tästä seuraa, että vain arvot tulevat kyseenalaiseksi ominaisarvoille .

- Sitä, joka täyttää, kutsutaan symmetriseksi. Esimerkkejä ovat elementit


-
 .
.
- Tason 2 kaikkien symmetristen tentoreiden joukko on merkitty symbolilla.

- Sitä, joka täyttää, kutsutaan epäsymmetriseksi tai vuorottelevaksi. Esimerkkejä ovat elementit


-
 .
.
- Kaikkien tason 2 epäsymmetristen tentoreiden joukko on merkitty symbolilla.

Avulla tensor toimivalta millään tasolla voidaan muodostaa. Vastaavasti voidaan määritellä lisää pareittain tapahtuvaa vaihtoa. Mutta nämä eivät ole enää toisistaan riippumattomia. Tällä tavalla jokainen sijaintien ja vaihtokeskusten vaihto ensimmäisen sijainnin kanssa voidaan jäljittää:





Injektiivinen ja projektiivinen tensorituote
Jos yhdessä jännitettävillä vektoreilla on topologia , on toivottavaa, että myös niiden tensorituotteella on topologia. On tietysti monia tapoja määritellä tällainen topologia. Injektiivinen ja projektiivinen tensorituote ovat kuitenkin luonnollinen valinta tähän.
Tensori -analyysi
Alun perin tensorilaskelmaa ei tutkittu tässä esitetyssä modernissa algebrallisessa käsityksessä, vaan se syntyi differentiaaligeometrian näkökohdista. Erityisesti Gregorio Ricci-Curbastro ja hänen oppilaansa Tullio Levi-Civita, joka kehitti sen. Tensorilaskuria kutsutaan siksi myös Ricci -laskimeksi. Albert Einstein otti laskennan käyttöön suhteellisuusteoriassaan , joka teki sen tunnetuksi ammattimaailmassa. Tuolloin käytettyjä tentoreita kutsutaan nykyään tensorikentiksi, ja niillä on edelleen tärkeä rooli differentiaaligeometriassa. Toisin kuin tenorit, tensorikentät ovat eriytettäviä kartoituksia, jotka osoittavat tensorin jokaiseen alla olevan (usein kaarevan) tilan pisteeseen.
Katso myös
kirjallisuus
-
Theodor Bröcker : Lineaarialgebra ja analyyttinen geometria. Birkhäuser, Basel 2004, ISBN 3-7643-2178-4 , luku . VII: Tensorikivi.
-
Ralph Abraham , Jerrold E. Marsden , T. Ratiu: Jakotukit, tensori -analyysi ja sovellukset (= Sovelletut matemaattiset tieteet. 75). 2. painos. Springer, New York NY et ai. 1998, ISBN 0-387-96790-7 .
-
Theodore Frankel : Fysiikan geometria. Esittely. Cambridge University Press, Cambridge et ai. 1997, ISBN 0-521-38334-X .
-
Horst Teichmann : Vektori- ja tensorilaskelmien fyysiset sovellukset (= BI -yliopistotaskut. 39). 3. Painos. Bibliographisches Institut , Mannheim et ai. 1973, ISBN 3-411-00039-2 .
-
André Lichnerowicz : Johdatus tensori -analyysiin (= BI -yliopiston taskukirja. 77). Bibliographisches Institut, Mannheim et ai. 1966.
-
Horst Lippmann : Sovellettu tensorilaskenta. Springer 1993.
- Mihail Itskov: Tensorialgebra ja tensori -analyysi insinööreille. 3. Painos. Springer, Heidelberg et ai. 2013, ISBN 978-3-642-30878-9 .
-
Adalbert Duschk : Tensorin käsite ja sen merkitys fysiikalle. Osa 1, 2, 3, Physikalische Blätter 1954, 1955, Osa 1, Geometriset perusteet, Osa 2, Tensalgebra, Osa 3, Tensoanalyysi.
-
Karin Reich : Tensorilaskennan kehitys. Absoluuttisesta differentiaalilaskennasta suhteellisuusteoriaan. Birkhäuser 1994 (historiasta).
nettilinkit
- Georg Bernhardt: Tietoja tenoreista, matriiseista ja pseudovektorista. PDF, saksa, 340 kB.
- Joseph C. Kolecki: Johdatus tenoreihin fysiikan ja tekniikan opiskelijoille. Johdanto oppilaiden tensorilaskimeen, PDF, englanti, 328 kB, NASA -julkaisu.
-
Eigenvalue-Eigenvector Glyphs: Visualizing Zeroth, Second, Fourth and Higher Order Tensors in Continuum. Verkkosivusto vektoreiden visualisointiin, englanti.
- Siegfried Petry: Johdatus tensorilaskimeen.
Yksilöllisiä todisteita
-
↑ elementary tensor (tai yksinkertainen tensor) kartoittuu numeerinen arvo (skalaari).
-
↑ MMG Ricci, T. Levi-Civita: methodes de calcul différentiel absolu et leurs sovelluksia. Julkaisussa: Mathematical Annals. 54, 1901, ISSN 0025-5831 , s. 125-201, verkossa.
-
^ John M. Lee: Johdatus sileisiin jakotukkeihin (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY et ai. 2003, ISBN 0-387-95448-1 , s. 172-179.
-
^ R. Abraham, Jerrold E. Marsden , T. Ratiu: Jakotukit, tensori -analyysi ja sovellukset (= Sovelletut matemaattiset tieteet 75). 2. painos. Springer, New York NY et ai. 1988, ISBN 0-387-96790-7, s. 338-339 .
-
^ Kerstin Weinberg: Luennon muistiinpanot. Tensalgebra ja analyysi. (PDF; 235 kB) Siegenin yliopisto , 24. lokakuuta 2012, käytetty 27. marraskuuta 2020 .
-
^ Heinz Schade, Klaus Neemann: Tensoanalyysi . 2. tarkistettu painos. de Gruyter, Berliini / New York 2006, ISBN 3-11-018943-7 , s. 277 ff .























































![{\ displaystyle {\ begin {matrix} L ^ {k} (E_ {1}, \ dotsc, E_ {k}; K) & {\ stackrel {\ sim} {\ longrightarrow}} & L (E_ {1} \ otimes \ dotsc \ otimes E_ {m}; E_ {m + 1} ^ {*} \ otimes \ dotsc \ otimes E_ {k} ^ {*}) \\\ lambda & \ longmapsto & \ left [\ lambda _ {(1, \ piste, m)} \ kaksoispiste v_ {1} \ otimes \ dotsc \ otimes v_ {m} \ mapsto \ lambda _ {(v_ {1}, \ piste, v_ {m})} \ in ( E_ {m + 1} \ otimes \ dotsc \ otimes E_ {k}) ^ {*} \ right] {\ text {,}} \\ && {\ text {where}} \ vasen [\ lambda _ {(v_ {1}, \ dotsc, v_ {m})} \ kaksoispiste (v_ {m + 1} \ otimes \ dotsc \ otimes v_ {k}) \ mapsto \ lambda (v_ {1}, \ piste, v_ {k} ) \ oikea] \\\ loppu {matriisi}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5af0ca5982fcea7f59fe2aa8996dd0c3de44ce0)



























































































































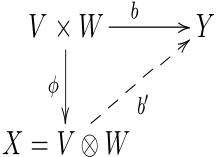




















































![{\ displaystyle \ psi: V_ {1} \ kertaa \ pistettä \ kertaa V_ {s} \ - [??]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/597d0dd2574ad69e6b77499917be8e727960cd06)































