Transitiivinen suhde

Transitiivisia kaksi ja ei-transitiivisuus (alhaalla oikealla), kuten suunnattuja graafeja esitetty

Transitiivisuus on matematiikka kaksinumeroisia suhde on määrä että kolme tekijää, jotka on ominaisuus , , määrä ja aina seuraa. Esimerkkejä transitiivisista suhteista ovat yhtäläiset ja pienemmät suhteet reaalilukuihin , koska kolmelle reaaliluvulle , sekä ja ja aina myös , sekä alkaen ja seuraa . ${\ displaystyle R}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle z}$${\ displaystyle xRy}$${\ displaystyle yRz}$${\ displaystyle xRz}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle z}$${\ displaystyle x = y}$${\ displaystyle y = z}$${\ displaystyle x = z}$${\ displaystyle x <y}$${\ displaystyle y <z}$${\ displaystyle x <z}$

Ei-transitiivista suhdetta kutsutaan intransitiiviseksi (ei pidä sekoittaa negatiiviseen transitiivisuuteen ). Transitiivisuus on yksi ekvivalenssisuhteen tai järjestyssuhteen edellytyksistä .

Muodollinen määritelmä

Jos on joukko ja kaksinumeroinen suhde , sen sanotaan olevan transitiivinen, jos (käyttäen infix-merkintää ) pätee: ${\ displaystyle M}$${\ displaystyle R \ subseteq M \ kertaa M}$${\ displaystyle M}$${\ displaystyle R}$

${\ displaystyle \ forall x, y, z \ muodossa M: xRy \ land yRz \ Rightarrow xRz.}$

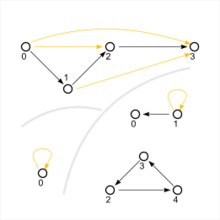
Esitys suunnattuna kaaviona

Missään suhteessa joukkoon voidaan pidettävä suunnattu graafi (katso esimerkki yllä). Kaavion solmut ovat elementin . Suunnattu reuna (nuoli ) vedetään solmusta solmuun , jos ja vain jos sovelletaan. ${\ displaystyle R}$${\ displaystyle M}$${\ displaystyle M}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle a \ longrightarrow b}$${\ displaystyle aRb}$

Transitiivisuutta voidaan nyt luonnehtia kaaviossa seuraavasti: Aina kun kaksi nuolta seuraa toisiaan ( ), on myös nuoli, joka yhdistää alku- ja loppusolmut suoraan ( ) (tämä pätee myös Hasse-kaavioon ). ${\ displaystyle R}$${\ displaystyle a \ longrightarrow b \ longrightarrow c}$${\ displaystyle a \ longrightarrow c}$

ominaisuudet

• Suhteen transitiivisuus mahdollistaa myös johtopäätösten tekemisen useista vaiheista (mikä voidaan helposti osoittaa täydellisellä induktiolla ): ${\ displaystyle R}$

  ${\ displaystyle a \, R \, b_ {1} \, R \, b_ {2} \, R \, \ pisteet \, R \, b_ {n} \, R \, c \ tarkoittaa \, R \, c}$

• Avulla, että ketjutus suhteiden, transitiivisuusehdon voidaan myös tunnettu siitä, että seuraava ehto: ${\ displaystyle \ circ}$

  ${\ displaystyle R \ circ R \ subseteq R}$

• Jos suhde on transitiivinen, tämä pätee myös käänteissuhteeseen . Esimerkkejä: suhde on liian käänteinen, suhde on liian käänteinen .${\ displaystyle R}$ ${\ displaystyle R ^ {- 1}}$${\ displaystyle \ leq}$${\ displaystyle \ geq}$${\ displaystyle <\}$${\ displaystyle> \}$
• Jos suhteet ja ovat transitiivisia, tämä pätee myös niiden risteykseen . Tämä lausunto voidaan yleistää kahdesta suhteesta minkä tahansa transitiivisten suhteiden perheen risteykseen .${\ displaystyle R}$${\ displaystyle S}$ ${\ displaystyle R \ cap S}$${\ displaystyle \ cap _ {i \ I} R_ {i}}$
• Jokaista mielivaltainen suhde on pienin transitiivisuus että sisältää ns transitiivinen kirjekuori on . Esimerkki: Olkoon edeltäjäsuhde luonnollisten numeroiden joukossa, joten se pätee . Suhde itsessään ei ole transitiivinen. Pienempi suhde johtuu transitiivisesta kirjekuoresta .${\ displaystyle R}$${\ displaystyle S}$${\ displaystyle R}$${\ displaystyle R}$
  ${\ displaystyle R}$${\ displaystyle a \, R \, b: \ Longleftrightarrow a = b-1}$${\ displaystyle R}$${\ displaystyle R}$${\ displaystyle <\}$

Esimerkkejä

Reaalilukujen järjestys

Kohdista a> b ja b> c seuraa a> c

Pienempi suhde on reaalilukuja on transitiivinen, koska se seuraa alkaen ja . Se on myös tiukka kokonaisjärjestys . ${\ displaystyle <\}$${\ displaystyle x <y}$${\ displaystyle y <z}$${\ displaystyle x <z}$

Samoin suhteet , ja ovat transitiivinen. ${\ displaystyle> \}$${\ displaystyle \ leq \}$${\ displaystyle \ geq \}$

Reaalilukujen yhtälö

Tavallinen reaalilukujen tasa-arvo on transitiivinen, koska se seuraa ja . Se on myös ekvivalenssisuhde . ${\ displaystyle = \}$${\ displaystyle x = y}$${\ displaystyle y = z}$${\ displaystyle x = z}$

Eriarvoisuus suhteessa todelliseen numeroita, ei kuitenkaan ole transitiivinen: ja , mutta tietenkään ei päde. ${\ displaystyle \ neq}$${\ displaystyle 3 \ neq 5}$${\ displaystyle 5 \ neq 3}$${\ displaystyle 3 \ neq 3}$

Kokonaislukujen jaettavuus

Jaollisuus suhde on kokonaislukuja on transitiivinen, koska se seuraa alkaen ja . Se on myös melkein tilaus . Jos rajoitat luonnollisten numeroiden joukkoa , saat osittaisen järjestyksen . ${\ displaystyle |}$${\ displaystyle a | b}$${\ displaystyle b | c}$${\ displaystyle a | c}$

Esimerkiksi ei ole transitiivinen yhteisarvo . Joten ja ovat kopriimi, aivan kuten ja kuitenkin, ja niillä on yhteinen tekijä . ${\ displaystyle 12}$${\ displaystyle 5}$${\ displaystyle 5}$${\ displaystyle 9}$${\ displaystyle 12}$${\ displaystyle 9}$ ${\ displaystyle 3}$

Alajoukko

Osajoukko suhde sarjaa on transitiivinen, koska se seuraa alkaen ja . Lisäksi on osittainen tilaus. ${\ displaystyle \ subseteq}$${\ displaystyle A \ subseteq B}$${\ displaystyle B \ subseteq C}$${\ displaystyle A \ subseteq C}$${\ displaystyle \ subseteq}$

Esimerkiksi joukkojen disjointness ei ole transitiivinen . Joten joukot ja ovat disjoint, aivan kuten ja , mutta ei ja (koska niillä on yhteinen elementti 1). ${\ displaystyle \ lbrace 1,2 \ rbrace}$${\ displaystyle \ lbrace 3 \ rbrace}$${\ displaystyle \ lbrace 3 \ rbrace}$${\ displaystyle \ lbrace 1,4 \ rbrace}$${\ displaystyle \ lbrace 1,2 \ rbrace}$${\ displaystyle \ lbrace 1,4 \ rbrace}$

Suorat viivat

On geometria , joka on yhdensuuntaisuus on suora transitiivisten: Jos sekä suora ja yhdensuuntainen, ja suorat linjat ja sitten myös ja samanaikaisesti. Lisäksi rinnakkaisuus on vastaavuussuhde. ${\ displaystyle g_ {1}}$${\ displaystyle g_ {2}}$${\ displaystyle g_ {2}}$${\ displaystyle g_ {3}}$${\ displaystyle g_ {1}}$${\ displaystyle g_ {3}}$

Vaikutus logiikkaan

On logiikka , transitiivisuusehdon koskee vaikutusta , jolloin tämä on myös tunnettu toimintatavasta Barbara on predikaattilogiikalla :

Alkaen ja seuraa (vertaa myös: leikkaussääntö ). ${\ displaystyle A \ Oikea nuoli B}$${\ displaystyle B \ Rightarrow C}$${\ displaystyle A \ Rightarrow C}$

Implikaatio määrittää kvasi-järjestyksen tarkasteltavan logiikan kaavoihin.

Katso myös

• Transitiivinen kirjekuori
• Negatiivinen transitiivisuus

nettilinkit

• Transitiivisuus . Julkaisussa: Michiel Hazewinkel (Toim.): Matematiikan tietosanakirja . Springer-Verlag ja EMS Press, Berliini 2002, ISBN 978-1-55608-010-4 (englanti, online ).