Pienimmän neliön menetelmä

Pienimmän neliösumman menetelmällä (lyhyt MKQ tai Englanti pienimmän neliösumman menetelmää , tai vain pienimmän neliösumman lyhyt: LS , ja rajaavat laajennuksia niistä johdettuja, kuten yleisen pienimmän neliösumman menetelmää , tai kaksivaiheinen pienimmän neliösumman menetelmällä sekä kutsutaan "tavallinen" ja lisäksi, että tavalliset pienimmät neliöt ( englanniksi tavalliset pienimmät neliöt , lyhyesti: OLS )) tai KQ -menetelmä ( pienimmän neliösumman summan poistettu menetelmä ) ovat matemaattiset standardimenettelyt oikaisua varten . Tässä tapauksessa, on joukko datapisteet toiminto , määrittää kulkee niin lähellä kuin mahdollista datapisteiden ja siten paras mahdollinen yhteenveto tiedot. Yleisimmin käytetty funktio on suora viiva , joka sitten sopiva viiva kutsutaan. Jotta menetelmää voidaan käyttää, toiminnon on sisällettävä vähintään yksi parametri . Nämä parametrit määritetään sitten menetelmällä siten, että kun funktiota verrataan datapisteisiin ja funktion arvon ja datapisteen välinen etäisyys neliöidään, näiden neliömatkojen summa on mahdollisimman pieni. Etäisyyksiä kutsutaan tällöin jäännöksiksi .

Tyypillisesti tätä menetelmää käytetään todellisten tietojen, kuten fyysisten tai taloudellisten mittausarvojen, tutkimiseen . Nämä tiedot sisältävät usein väistämättömiä mittausvirheitä ja vaihteluita . Jos oletetaan, että mitatut arvot ovat lähellä taustalla olevia " todellisia arvoja " ja että mitattujen arvojen välillä on tietty suhde, menetelmää voidaan käyttää funktion löytämiseen, joka kuvaa tämän datasuhteen mahdollisimman hyvin . Menetelmää voidaan käyttää myös käänteisesti eri toimintojen testaamiseen ja siten kuvaamaan tuntematonta suhdetta tiedoissa.

Esimerkkigrafiikassa syötetään datapisteitä ja kompensointitoiminto. Valitaan yleinen toiminto ( mallitoiminto ), joka vastaa kysymystä ja tietoja, tässä logistinen funktio . Niiden parametrit määritetään nyt siten, että havaintojen neliöpoikkeamien summa funktion arvoista minimoidaan . Kuvassa poikkeama tässä kohdassa voidaan nähdä pystysuorana etäisyytenä havainnon ja käyrän välillä. ${\ displaystyle e}$${\ displaystyle y}$${\ displaystyle e}$${\ displaystyle x}$${\ displaystyle y}$

In stokastiikan , pienimmän neliösumman menetelmällä on useimmiten käytetään regressio analyysi arviointimenetelmä , jossa se on myös nimitystä pienimmän neliösumman estimointiin tai pienimmän neliösumman estimoinnin . Koska pienimmän neliösumman estimaatti, jäännössumma minimoitu, se on se arviointimenetelmä, joka käsittää määrityksen maksimoinnin. Menetelmällä pienimmän neliösumman käytetään , kuten järjestelmän tunnistus yhteydessä mallikokeet esim. B. insinööreille tie ulos paradoksaalisesta tilanteesta, jossa määritetään tuntemattomien lakien malliparametrit.

tarina

Uudenvuodenpäivänä 1801 italialainen tähtitieteilijä Giuseppe Piazzi löysi kääpiöplaneetan Ceres . Hän pystyi seuraamaan polkua 40 päivää, sitten Ceres katosi auringon taakse. Vuoden aikana monet tiedemiehet yrittivät epäonnistuneesti laskea kiertorataa Piazzin havaintojen perusteella - olettaen ympyrän kiertoradan, koska tuolloin kiertoradan elementit voitiin määrittää vain matemaattisesti sellaisten havaittujen taivasasentojen perusteella .

24-vuotias Gauss onnistui laskemaan kiertoradan uuden epäsuoran kiertoradan määrittämismenetelmän ja korvauslaskelmiensa avulla, jotka perustuivat pienimmän neliösumman menetelmään (vaikka sitä ei ole vielä merkitty) siten, että Franz Xaver von Zach löysi hänet 7. joulukuuta 1801 ja - vahvistettu - 31. joulukuuta 1801. Heinrich Wilhelm Olbers vahvisti tämän Zachista riippumatta havainnoilla 1. ja 2. tammikuuta 1802.

Ongelma Cererin löytämisessä sellaisenaan oli se, että havainnot eivät tehneet sijaintia, osaa kiertoradasta tai etäisyyttä , vain havainnon suunnat . Tämä johtaa ellipsin etsimiseen eikä ympyrään Gaussin kilpailijoiden ehdottamalla tavalla. Yksi ellipsin polttopisteistä on tiedossa ( aurinko itse), ja Ceresin kiertoradan kaaret tarkkailusuuntien välillä kulkevat Keplerin toisen lain mukaisesti , toisin sanoen ajat käyttäytyvät kuten ohjauspalkki. Lisäksi laskennallisesta ratkaisusta tiedetään, että havainnot itsessään ottavat avaruuden kartiomaisen osan, maapallon kiertorata.

Periaatteessa ongelma johtaa kahdeksannen asteen yhtälöön, jonka triviaali ratkaisu on maan kierto. Laajojen toissijaisten olosuhteiden ja (myöhemmin) Gaussin kehittämän pienimmän neliön menetelmän avulla 24-vuotias onnistui määrittämään sijainnin, jonka hän oli laskenut Ceresin kiertoradalle 25. marraskuuta-31. joulukuuta 1801. Tämän ansiosta Zach löysi Ceresin ennusteen viimeisenä päivänä. Paikka oli vähintään 7 astetta (eli 13,5  täysikuun leveyttä ) itään siitä paikasta, missä muut tähtitieteilijät olivat epäilleet Ceresiä, jota paitsi Zach, myös Olbers kunnioittivat.

Hänen ensimmäiset laskelmansa olivat edelleen ilman pienimmän neliösumman menetelmää , vasta kun paljon uutta tietoa tuli saataville Ceresin uudelleen löytämisen jälkeen, hän käytti niitä kiertorataelementtien tarkempaan määrittämiseen, mutta paljastamatta yleisesti menetelmänsä yksityiskohtia. Myös Piazzin maine, joka oli kärsinyt vakavasti polkupisteistään, jotka eivät halunneet sovittaa pyöreää polkua, palautettiin.

Pienimpien neliöiden menetelmän edeltäjä on pienimpien absoluuttisten poikkeamien menetelmä , jonka Rugjer Josip Bošković kehitti vuonna 1760 . Gauss oli kehittänyt pienimmän neliösumman menetelmän perusteet jo vuonna 1795 18 -vuotiaana. Se perustui Pierre-Simon Laplacen ajatukseen laskea mitattujen arvojen poikkeamat odotetusta arvosta siten, että kaikkien näiden niin kutsuttujen virheiden summa johti nollaan. Toisin kuin tämä menetelmä, Gauss käytti virheen sijaan neliöitä ja pystyi luopumaan nollasummavaatimuksesta. Gaussista riippumatta ranskalainen Adrien-Marie Legendre kehitti saman menetelmän, julkaisi sen ensimmäisen kerran vuonna 1805, pienen komeetan kiertoradan laskennan lopussa, ja julkaisi siitä toisen tutkielman vuonna 1810. Sen esitys oli erittäin selkeä. ja yksinkertainen. Nimi Méthode des moindres carrés (pienimpien neliöiden menetelmä) tulee myös Legendresta .

Vuonna 1809 Gauss julkaisi taivaallisen mekaanisen teoksensa Theoria motus corporum coelestium toisessa osassa sectionibus conicis solem ambientium (teoria auringon taivasta kiertävien taivaankappaleiden liikkeestä), menetelmä sisältäen normaalit yhtälöt, sekä Gaussin eliminointimenetelmä ja Gauss-Newton-menetelmä , joka ylitti paljon Legendren. Siinä hän viittasi löytökseen pienimmän neliösumman menetelmään ja väitti löytäneensä ja soveltaneensa sitä jo vuonna 1795 (eli ennen Legendrea), mikä ärsytti häntä pitkään. Legendre valitti tästä Gaussille lähettämässään pitkässä kirjeessä, johon Gauss ei vastannut. Gauss viittasi vain satunnaisesti merkintään matemaattisessa päiväkirjassaan 17. kesäkuuta 1798 (latinaksi on salainen lause: Calculus probabilitatis contra La Place defensus ( Laplacea vastaan ​​puolustettu todennäköisyyslaskuri) eikä mitään muuta). Laplace arvioi asian siten, että Legendre julkaisi ensimmäisen julkaisun, mutta Gauss tiesi epäilemättä menetelmän etukäteen, käytti sitä itse ja välitti sen myös muille tähtitieteilijöille kirjeitse. Pienimmän neliösumman menetelmästä tuli nopeasti vakiomenetelmä tähtitieteellisten tai geodeettisten aineistojen käsittelyyn sen julkaisemisen jälkeen.

Gauss käytti menetelmää intensiivisesti hänen tutkimuksessa kuningaskunnan Hannoverin vuoteen triangulaation . Kaksiosainen teos julkaistiin vuosina 1821 ja 1823, ja vuonna 1826 täydennys Theoria Combinationis observum erroribus minimis obnoxiae (teoria pienimpien virheiden kohteena olevien havaintojen yhdistelmästä) , jossa Gauss perusteli pienimmän neliösumman menetelmän menestyksen se, että sitä verrattiin muihin menetelmiin, oikaisulaskelma on laaja -alaisesti optimaalinen. Matemaattinen muotoilu Tämän lausunnon kutsutaan lause, Gauss-Markow nimetty Andrei Andrejewitsch Markow , joka löysi ja teki suosituksi tämä osa Gauss työtä, joka oli aluksi huomiotta, 1900-luvulla (katso myös lauseen Gauss-Markow # Geschichte ). Theoria Combinationis sisältää myös menetelmiä tehokkaasti ratkaista lineaariset yhtälöryhmät , kuten Gauß-Seidel menetelmä ja LR hajoaminen , joka edustaa merkittävää edistystä on matemaattinen tieto ajasta.

Ranskalainen maanmittausviranomainen André-Louis Cholesky kehitti Choleskyn hajoamisen ensimmäisen maailmansodan aikana , mikä taas tuotti huomattavan tehokkuuden lisäyksen Gaussin ratkaisumenetelmään verrattuna. 1960 -luvulla Gene Golub kehitti ajatuksen ratkaista esiintyvät lineaariset yhtälöjärjestelmät käyttämällä QR -hajoamista .

Toimintatapa

vaatimukset

Tarkastellaan riippuvaista muuttujaa , johon yksi tai useampi muuttuja vaikuttaa. Jousen venymä riippuu vain käytetystä voimasta, mutta yrityksen kannattavuus riippuu useista tekijöistä, kuten myynnistä , erilaisista kustannuksista tai pääomasta . Merkintöjen yksinkertaistamiseksi esitys rajoittuu yhteen muuttujaan seuraavassa . Suhde ja muuttujat määräytyy mallifunktion , esimerkiksi paraabelin tai eksponentiaalisen funktion avulla${\ displaystyle y}$${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle f}$

${\ displaystyle y (x) = f (x; \ alpha _ {1}, \ dotsc, \ alpha _ {m})}$,

joka riippuu sekä toiminnalliset parametrit. Tämä toiminto tulee joko käyttäjän tietämyksestä tai enemmän tai vähemmän aikaa vievästä mallin etsimisestä; erilaisia ​​mallitoimintoja on ehkä sovellettava ja tuloksia on verrattava. Yksinkertainen tapaus, joka perustuu olemassa olevaan tietoon, on esimerkiksi jousi, koska tässä on Hooken laki ja siten lineaarinen funktio, jossa ainoa parametri on jousivakio . Vaikeammissa tapauksissa, kuten yrityksen, toiminnon tyypin valinnan on kuitenkin edeltettävä monimutkaista mallinnusprosessia . ${\ displaystyle x}$${\ displaystyle m}$${\ displaystyle \ alpha _ {j}}$

Tietojen saamiseksi parametreista ja siten tietystä suhteesta kerätään vastaavat havaintoarvot riippumattomien muuttujien vastaaville arvoille . Parametreja käytetään valitun toimintotyypin mukauttamiseen näihin havaittuihin arvoihin . Tavoitteena on nyt valita parametrit siten, että mallitoiminto lähentää tietoja mahdollisimman hyvin. ${\ displaystyle n}$${\ displaystyle x_ {i}}$${\ displaystyle x}$${\ displaystyle y_ {i}}$ ${\ displaystyle (i = 1, \ piste, n)}$${\ displaystyle \ alpha _ {j}}$${\ displaystyle y_ {i}}$${\ displaystyle \ alpha _ {j}}$

Gaussin ja Legendren idea oli tehdä jakeluehdotuksia näiden havaintoarvojen mittausvirheistä. Niiden pitäisi olla keskimäärin nolla, niiden vaihteluväli on vakio ja niiden on oltava stokastisesti riippumattomia kaikista muista mittausvirheistä . Tämä tarkoittaa sitä, että mittausvirheissä ei enää ole systemaattista tietoa, eli että ne vaihtelevat nollan ympäri puhtaasti sattumalta. Lisäksi mittausvirheet tulisi jakaa normaalisti , mikä toisaalta tarjoaa todennäköisyysetuja ja toisaalta takaa, että poikkeamat ovat yhtä hyviä kuin poissuljettuja. ${\ displaystyle y}$

Näiden olettamusten parametrien määrittämiseksi on yleensä tarpeen, että datapisteitä on huomattavasti enemmän kuin parametreja, joten sitä on sovellettava. ${\ displaystyle \ alpha _ {j}}$${\ displaystyle n> m}$

Virheiden neliöiden summan minimointi

Lähestymisen määrittämisperuste on valittava siten, että suuret mallifunktion poikkeamat tiedoista painotetaan enemmän kuin pienet. Jos mikään ratkaisu ei ole mahdollinen ilman poikkeamia, pienin kokonaispoikkeama oleva kompromissi on paras yleisesti sovellettava kriteeri.

Tätä tarkoitusta varten virheiden neliöiden summa, jota kutsutaan myös virheiden neliöiden summaksi (tarkemmin sanottuna: jäännösten neliöiden summa), määritellään virheiden neliöerojen summana. mallikäyrän ja tietojen arvot . ${\ displaystyle f (x_ {i})}$${\ displaystyle y_ {i}}$

Kaavamerkinnässä parametrien ja tulosten kanssa ${\ displaystyle {\ vec {\ alpha}} = (\ alfa _ {1}, \ alpha _ {2}, \ pisteitä, \ alpha _ {m}) \ in \ mathbb {R} ^ {m}}$${\ displaystyle {\ vec {f}} = (f (x_ {1}, {\ vec {\ alfa}}), \ pisteitä, f (x_ {n}, {\ vec {\ alpha}})) \ \ mathbbissa {R} ^ {n}}$

${\ displaystyle \ summa _ {i = 1} ^ {n} (f (x_ {i}, {\ vec {\ alpha}}) - y_ {i}) ^ {2} = \ | {\ vec {f }} - {\ vec {y}} \ | _ {2} ^ {2}.}$

Sitten on valittava ne parametrit , joiden neliösäätövirheiden summa on minimaalinen: ${\ displaystyle \ alpha _ {j}}$

${\ displaystyle \ min _ {\ vec {\ alpha}} \ | {\ vec {f}} - {\ vec {y}} \ | _ {2} ^ {2}.}$

Miten tämä minimointitehtävä ratkaistaan, riippuu mallitoiminnon tyypistä.

Jos ulkoisen tietojoukon virheen neliösumma ennustetaan, puhutaan PRESS -tilastoista ( englanninkielinen ennustava jäännössumma ).

Lineaarinen mallitoiminto

Lineaariset mallitoiminnot ovat mielivaltaisten, yleensä epälineaaristen perustoimintojen lineaarisia yhdistelmiä . Tällaisissa mallitoiminnoissa minimointitehtävä voidaan ratkaista myös analyyttisesti käyttämällä ääriarvomenetelmää ilman iteratiivisia lähentämisvaiheita. Ensin esitetään muutamia yksinkertaisia ​​erikoistapauksia ja esimerkkejä.

Yksinkertaisen lineaarisen parhaiten sopivan suoran erikoistapaus

Johtaminen ja menettely

Ensimmäisen kertaluvun polynomi on yksinkertainen mallitoiminto, jossa on kaksi lineaarista parametria

${\ displaystyle f (x) = \ alpha _ {0} + \ alpha _ {1} x}$

Etsimme kertoimia ja parhaiten sopivaa suoraa annetuille mittausarvoille . Poikkeamat etsimäsi suoran ja vastaavien mittausarvojen välillä ${\ displaystyle n}$${\ displaystyle (x_ {1}, y_ {1}), \ piste, (x_ {n}, y_ {n})}$${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$${\ displaystyle r_ {i}}$

${\ displaystyle {\ begin {matrix} r_ {1} = & \ alpha _ {0} + & \ alpha _ {1} x_ {1} -y_ {1} \\ r_ {2} = & \ alpha _ { 0} + & \ alfa _ {1} x_ {2} -y_ {2} \\\ vdots & \ vdots & \ vdots \\ r_ {n} = & \ alpha _ {0} + & \ alfa _ {1 } x_ {n} -y_ {n} \\\ end {matrix}}}$

kutsutaan sovitusvirheiksi tai jäännöksiksi . Etsimme nyt kertoimia ja pienintä virheiden neliöiden summaa ${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ min _ {\ alpha _ {0}, \ alpha _ {1}} \ sum _ {i = 1} ^ {n} r_ {i} ^ {2}}$.

Tämän virheiden neliön lähestymistavan suuri etu tulee näkyviin, kun tämä minimointi suoritetaan matemaattisesti: Summafunktio ymmärretään kahden muuttujan funktiona ja (tulevat mittausarvot ovat numeerisia vakioita), sitten johdannainen (tarkemmin sanottuna: osittaiset johdannaiset ) funktiosta perustuen näihin muuttujiin (eli ja ) ja lopulta etsinyt nollapistettä tästä derivaatasta . Tuloksena on lineaarinen yhtälöjärjestelmä${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle {\ begin {aligned} \ texttyle n \ cdot \ alpha _ {0} + \ vasen (\ sum \ limits _ {i = 1} ^ {n} x_ {i} \ oikea) \ alpha _ {1 } & = \ texttyle \ sum \ limits _ {i = 1} ^ {n} y_ {i} \\\ texttyle \ left (\ sum \ limits _ {i = 1} ^ {n} x_ {i} \ oikea ) \ alpha _ {0} + \ vasen (\ sum \ limits _ {i = 1} ^ {n} x_ {i} ^ {2} \ oikea) \ alpha _ {1} & = \ texttyle \ sum \ limits _ {i = 1} ^ {n} x_ {i} y_ {i} \ end {aligned}}}$

liuoksen kanssa

${\ displaystyle \ alpha _ {1} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) y_ {i}} {\ summa \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n } (x_ {i} - {\ overline {x}}) (y_ {i} - {\ overline {y}})} {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} = {\ frac {SP_ {xy}} {SQ_ {x}}}}$ja ,${\ displaystyle \; \ alpha _ {0} = {\ overline {y}} - \ alpha _ {1} {\ overline {x}}}$

jossa edustaa summa tuotteiden poikkeamien välillä ja , ja se edustaa neliöityjen poikkeamat on . Se on aritmeettinen keskiarvo on arvojen, vastaavasti. Ratkaisu voi löytyä myös ei- keskitettynä muodossa avulla ja siirtymän lause${\ displaystyle SP_ {xy}}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle SQ_ {x}}$${\ displaystyle x}$${\ displaystyle \ texttyle {\ overline {x}} = {\ frac {1} {n}} \ sum \ nolimits _ {i = 1} ^ {n} x_ {i}}$${\ displaystyle x}$${\ displaystyle {\ overline {y}}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ alpha _ {1} = {\ frac {\ sum _ {i = 1} ^ {n} (x_ {i} y_ {i}) - n {\ overline {x}} {\ overline {y }}} {\ vasen (\ summa _ {i = 1} ^ {n} x_ {i} ^ {2} \ oikea) -n {\ overline {x}} ^ {2}}}}$

voidaan määrittää. Nämä tulokset voidaan myös johtaa reaalimuuttujan funktioilla, ts. Ilman osittaisia ​​derivaattoja.

Esimerkki parhaiten sopivasta suorasta viivasta

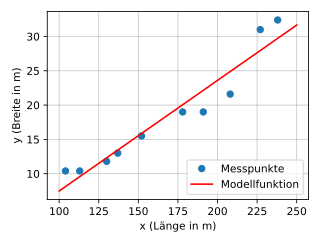
Tässä esimerkissä lasketaan muodon parhaiten sopiva suora viiva, joka näyttää tietojoukon kahden ominaisuuden välisen suhteen. Tietojoukko koostuu kymmenen sota -aluksen pituudesta ja leveydestä (katso sota -aluksen tiedot ). Leveysaste tulisi yrittää yhdistää pituusasteeseen. Tiedot on esitetty seuraavan taulukon kolmessa ensimmäisessä sarakkeessa. Muut sarakkeet liittyvät välituloksiin parhaiten sopivan suoran laskemiseksi. Muuttujan tulee osoittaa sota -aluksen pituus ja leveys. Etsimme suoraa viivaa , jolle jos käytetään tunnettuja arvoja , funktion arvot ovat mahdollisimman lähellä tunnettuja arvoja . ${\ displaystyle f (x) = \ alpha _ {0} + \ alpha _ {1} x}$${\ displaystyle x_ {i}}$${\ displaystyle i}$${\ displaystyle y_ {i}}$${\ displaystyle f (x) = y = \ alpha _ {0} + \ alpha _ {1} x}$${\ displaystyle x_ {i}}$${\ displaystyle f (x_ {i}) = {\ tilde {y}} _ {i}}$${\ displaystyle y_ {i}}$

Sotalaiva	Pituus (m)	Leveys (m)	${\ displaystyle (x_ {i} - {\ overline {x}})}$	${\ displaystyle (y_ {i} - {\ overline {y}})}$
${\ displaystyle i}$	${\ displaystyle x_ {i}}$	${\ displaystyle y_ {i}}$	${\ displaystyle x_ {i} ^ {*}}$	${\ displaystyle y_ {i} ^ {*}}$	${\ displaystyle x_ {i} ^ {*} \ cdot y_ {i} ^ {*}}$	${\ displaystyle (x_ {i} ^ {*}) ^ {2}}$	${\ displaystyle f (x_ {i})}$	${\ displaystyle f (x_ {i}) - y_ {i}}$
1	208	21.6	40.2	3.19	128,24	1616,04	24,88	3.28
2	152	15.5	−15,8	-2,91	45,98	249,64	15,86	0,36
3	113	10.4	−54,8	−8,01	438,95	3003,04	9.57	-0,83
4	227	31,0	59.2	12.59	745,33	3504,64	27,95	−3,05
5	137	13.0	−30,8	−5,41	166,63	948,64	13.44	0,44
6	238	32.4	70.2	13,99	982,10	4928,04	29.72	-2,68
7	178	19,0	10.2	0,59	6.02	104,04	20.05	1.05
8	104	10.4	−63,8	−8,01	511,04	4070,44	8.12	-2,28
9	191	19,0	23.2	0,59	13.69	538,24	22.14	3.14
10	130	11.8	−37,8	−6,61	249,86	1428,84	12.31	0,51
Summa Σ	1678	184.1			3287,72	20391,60

Parhaiten sopiva viiva määräytyy kertoimien avulla ja ne lasketaan edellä kuvatulla tavalla ${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ alpha _ {1} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) (y_ {i} - {\ overline {y}})} {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} = {\ frac {SP_ {xy }} {SQ_ {x}}}}$

${\ displaystyle \ alpha _ {0} = {\ overline {y}} - \ alpha _ {1} {\ overline {x}}}$

Vakiot ja ovat vastaavasti keskiarvoja ja - ja mittarit, niin ${\ displaystyle {\ overline {x}}}$${\ displaystyle {\ overline {y}}}$${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle {\ overline {x}} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} x_ {i}} {n}} = {\ frac {1678} {10}} = 167 {,} 8}$

${\ displaystyle {\ overline {y}} = {\ frac {184.1} {10}} = 18 {,} 41}$

Ensimmäisenä välivaiheena voidaan nyt laskea poikkeama keskiarvosta kullekin sota -alukselle: ja - nämä arvot merkitään yllä olevan taulukon neljänteen ja viidenteen sarakkeeseen. Tämä yksinkertaistaa kaavaa${\ displaystyle x_ {i} ^ {*} = (x_ {i} - {\ overline {x}})}$${\ displaystyle \; y_ {i} ^ {*} = (y_ {i} - {\ overline {y}})}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ alpha _ {1} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} x_ {i} ^ {*} \ cdot y_ {i} ^ {*}} {\ summa \ nolimits _ {i = 1} ^ {n} (x_ {i} ^ {*}) ^ {2}}}}$

Toisena välivaiheena tuotteet ja voidaan laskea kullekin sota -alukselle. Nämä arvot syötetään taulukon kuudenteen ja seitsemänteen sarakkeeseen, ja ne voidaan nyt helposti laskea yhteen. Tämä voidaan laskea muodossa ${\ displaystyle x_ {i} ^ {*} \ cdot y_ {i} ^ {*}}$${\ displaystyle (x_ {i} ^ {*}) ^ {2}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ alpha _ {1} = {\ frac {3287 {,} 82} {20391 {,} 60}} = 0 {,} 1612}$

Arvo voidaan jo tulkita: Jos oletetaan, että tiedot liittyvät lineaarisesti ja ne voidaan kuvata lasketulla parhaiten sopivalla rivillämme, sota-aluksen leveys kasvaa noin 0,16 metriä jokaista pidempää metriä kohti. ${\ displaystyle \ alpha _ {1}}$

Sieppaus on sitten ${\ displaystyle \ alpha _ {0}}$

${\ displaystyle \ alpha _ {0} = {\ overline {y}} - \ alpha _ {1} {\ overline {x}} = 18 {,} 41-0 {,} 1612 \ cdot 167 {,} 8 = -8 {,} 6451}$

Sopivimman viivan yhtälö on siis ${\ displaystyle f (x) = - 8 {,} 6451 + 0 {,} 1612x}$

Tämän havainnollistamiseksi tiedot voidaan piirtää sirontakaaviona ja lisätä parhaiten sopiva viiva. Kaavio viittaa siihen, että sota -aluksen pituuden ja leveyden välillä on todellakin lineaarinen suhde näytetiedoissamme. Pisteiden säätö on varsin hyvä. Suoralla ennustettujen arvojen poikkeama mitatuista arvoista voidaan myös nähdä mittauksena . Vastaavat arvot syötetään taulukon kahdeksanteen ja yhdeksänteen sarakkeeseen. Keskimääräinen poikkeama on 2,1 m. Määrityskerroin vakioiduna kertoimena antaa myös arvon noin 92,2% (100% vastaa 0 m: n keskimääräistä poikkeamaa); laskenta, katso esimerkki määrityskertoimesta . ${\ displaystyle f (x_ {i}) - y_ {i}}$${\ displaystyle f (x_ {i})}$${\ displaystyle y_ {i}}$

Negatiivinen sieppaus tarkoittaa kuitenkin sitä, että lineaarisessa mallissamme 0 metrin pituisen sota -aluksen leveys on negatiivinen - tai sota -alukset alkavat olla olemassa vain tietyltä vähimmäispituudelta. Todellisuuteen verrattuna tämä on tietysti väärin, mikä voidaan ottaa huomioon arvioitaessa tilastollista analyysiä. On todennäköistä, että malli pätee vain sille alueelle, jolta mittausarvot ovat todellisuudessa saatavilla (tässä tapauksessa sota -alusten pituudet välillä 100 m - 240 m) ja että alueen ulkopuolella lineaarinen funktio ei enää sovellu edustamaan tiedot. ${\ displaystyle \ alpha _ {0}}$

Yksinkertaiset polynomi parhaiten sopivat käyrät

Parhaiten sopivat polynomit ovat yleisempiä kuin lineaarisesti parhaiten sopivat viivat

${\ displaystyle y (x) \ kb \ alpha _ {0} + \ alpha _ {1} x + \ alfa _ {2} x ^ {2} + \ piste + + alfa {{}} x ^ {q} }$,

jota kuvataan nyt esimerkin avulla (tällaiset tasauspolynomi -lähestymistavat voidaan - iteratiivisen ratkaisun lisäksi - ratkaista analyyttisesti käyttämällä ääriarvomenetelmää).

Tulokset microcensus tekemän selvityksen Liittovaltion tilastokeskuksen ovat keskimäärin painot miesten ikäryhmittäin (lähde: Liittovaltion tilastokeskuksen Wiesbaden 2009). Analyysiä varten ikäryhmät korvattiin keskiluokilla. Muuttuvan painon ( ) riippuvuus muuttuvasta iästä ( ) on analysoitava. ${\ displaystyle y}$${\ displaystyle x}$

Sironta kaavio ehdottaa noin parabolinen suhde ja , joita voidaan usein arvioida hyvin käyttämällä polynomia. Siitä tulee lomakkeen polynominen lähestymistapa ${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle y (x) \ kb \ alpha _ {0} + \ alpha _ {1} x + \ alfa _ {2} x ^ {2} + \ alpha _ {3} x ^ {3} + \ alpha _ {4} x ^ {4}}$

yrittää. Ratkaisu on neljännen asteen polynomi

${\ displaystyle y (x) \ noin 47 {,} 86 + 2 {,} 2x -0 {,} 04809x ^ {2} +0 {,} 0004935x ^ {3} -0 {,} 000002148x ^ {4} }$.

Mittauspisteet poikkeavat keskimäärin ( keskihajonta ) 0,19 kg mallitoiminnosta. Jos pienennät polynomin asteen 3: ksi, saat ratkaisun

${\ displaystyle y (x) \ noin 54 {,} 22 + 1 {,} 515x-0 {,} 0226x ^ ​​{2} +0 {,} 0001002x ^ {3}}$

keskimääräinen poikkeama 0,22 kg ja polynomi -aste 2 ratkaisu

${\ displaystyle y (x) \ noin 61 {,} 42 + 0 {,} 9397x-0 {,} 008881x ^ {2}}$

keskimääräinen poikkeama 0,42 kg. Kuten voidaan nähdä, jos korkeammat termit jätetään pois, alempien termien kertoimet muuttuvat. Menetelmä yrittää saada parhaan hyödyn jokaisesta tilanteesta. Vastaavasti puuttuvat korkeammat termit kompensoidaan mahdollisimman hyvin alempien termien avulla, kunnes matemaattinen optimi saavutetaan. Toisen asteen polynomi (parabola) kuvaa hyvin mittauspisteiden kulkua (katso kuva).

Erikoistapaus lineaarisesta säätötoiminnosta, jossa on useita muuttujia

Jos mallitoiminto on ensimmäisen kertaluvun moniulotteinen polynomi eli jos sillä on useita itsenäisiä mallimuuttujia vain yhden muuttujan sijasta, saadaan muodon lineaarinen funktio ${\ displaystyle x}$${\ displaystyle x_ {1}, \ ldots, x_ {N}}$

${\ displaystyle f (x_ {1}, \ dotsc, x_ {N}; \ alpha _ {0}, \ alpha _ {1}, \ dotsc, \ alpha _ {N}) = \ alpha _ {0} + \ alfa _ {1} x_ {1} + \ piste + + alfa _ {N} x_ {N}}$,

ne, jotka ovat jäännöksissä

${\ displaystyle {\ begin {matrix} r_ {1} = & \ alpha _ {0} + \ alpha _ {1} x_ {1,1} + & \ dotsb \; \; + \ alpha _ {j} x_ {j, 1} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, 1} -y_ {1} \\ r_ {2} = α _ {0} + \ alfa _ {1} x_ {1,2} + & \ pisteitä \; \; + \ alpha _ {j} x_ {j, 2} + & \ pisteitä \; \; + \ alfa _ {N} x_ {N, 2} -y_ {2} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {i} = & \ alpha _ {0} + \ alpha _ {1} x_ {1, i} + & \ pisteitä \; \ ; + \ alpha _ {j} x_ {j, i} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, i} -y_ {i} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {n} = α _ {0} + \ alpha _ {1} x_ {1, n} + & \ dotsb \; \; + \ alpha _ {j} x_ {j, n} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, n} -y_ {n} \\\ end {matrix}}}$

ja minimointimenetelmästä

${\ displaystyle \ min _ {\ alpha} \ summa _ {i = 1} ^ {n} r_ {i} ^ {2}}$

voidaan ratkaista.

Yleinen lineaarinen tapaus

Seuraavassa esitetään minkä tahansa ulottuvuuden omaavien lineaaristen mallitoimintojen yleinen tapaus. Tietylle mitatulle arvotoiminnolle

${\ displaystyle y (x_ {1}, x_ {2}, \ pisteitä, x_ {N})}$

kanssa riippumattomia muuttujia on optimaalisesti sovitettu lineaarinen malli funktio ${\ displaystyle N}$

${\ displaystyle f (x_ {1}, x_ {2}, \ dots, x_ {N}; \ alpha _ {1}, \ alpha _ {2}, \ dots, \ alpha _ {m}) = \ summa _ {j = 1} ^ {m} \ alpha _ {j} \ varphi _ {j} (x_ {1}, x_ {2}, \ pisteitä, x_ {N})}$

haluttu, jonka neliöpoikkeaman tulisi olla minimaalinen. ovat toimintokoordinaatit, määritettävät lineaariset saapuvat parametrit ja mahdolliset lineaarisesti riippumattomat funktiot, jotka on valittu ongelmaa varten. ${\ displaystyle x_ {i}}$${\ displaystyle \ alpha _ {j}}$${\ displaystyle \ varphi _ {j}}$

Tietyissä mittauspisteissä ${\ displaystyle n}$

${\ displaystyle (x_ {1,1}, x_ {2,1}, \ pisteitä, x_ {N, 1}; y_ {1}), (x_ {1,2}, x_ {2,2}, \ pisteitä, x_ {N, 2}; y_ {2}), \ pisteitä, (x_ {1, n}, x_ {2, n}, \ pisteitä, x_ {N, n}; y_ {n})}$

yksi saa säätövirheet

${\ displaystyle {\ begin {matrix} r_ {1} = & \ alpha _ {1} \ varphi _ {1} (x_ {1,1}, \ pisteitä, x_ {N, 1}) \; \; + α _ {2} \ varphi _ {2} (x_ {1,1}, \ pisteitä, x_ {N, 1}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ { m} (x_ {1,1}, \ pisteitä, x_ {N, 1}) - y_ {1} \\ r_ {2} = & \ alfa _ {1} \ varphi _ {1} (x_ {1, 2}, \ pisteitä, x_ {N, 2}) \; \; + α _ {2} \ varphi _ {2} (x_ {1,2}, \ pisteitä, x_ {N, 2}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ {m} (x_ {1,2}, \ dots, x_ {N, 2}) - y_ {2} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {i} = & \ alpha _ {1} \ varphi _ {1} (x_ {1, i}, \ pisteitä, x_ {N, i}) \; \; + α _ {2} \ varphi _ {2} (x_ {1, i}, \ pisteitä, x_ {N, i}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ {m } (x_ {1, i}, \ pisteitä, x_ {N, i}) - y_ {i} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {n} = & \ alfa _ {1 } \ varphi _ {1} (x_ {1, n}, \ pisteitä, x_ {N, n}) \; \; + & \ alfa _ {2} \ varphi _ {2} (x_ {1, n} , \ pisteitä, x_ {N, n}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ {m} (x_ {1, n}, \ pisteitä, x_ {N, n }) - y_ {n} \\\ end {matrix}}}$

tai matriisimerkinnöissä

${\ displaystyle r = A \ alpha -y,}$

jossa vektori, joka tekee yhteenvedon siitä, mikä matriisi perusfunktion arvot , parametrivektori , parametrit ja vektorin havainnot missä . ${\ displaystyle r \ in \ mathbb {R} ^ {n}}$${\ displaystyle r_ {i}}$ ${\ displaystyle A \ \ mathbb {R} ^ {n \ times m}}$${\ displaystyle A_ {ij}: = \ varphi _ {j} (x_ {1, i}, \ pisteitä, x_ {N, i})}$${\ displaystyle \ alpha \ in \ mathbb {R} ^ {m}}$${\ displaystyle \ alpha _ {j}}$${\ displaystyle y \ in \ mathbb {R} ^ {n}}$${\ displaystyle y_ {i}}$${\ displaystyle n \ geq m}$

Minimointiongelma käyttämällä euklidista normia mennessä

${\ displaystyle \ min _ {\ alpha} \ summa _ {i = 1} ^ {n} r_ {i} ^ {2} = \ min _ {\ alpha} \ | f (\ alpha) -y \ | _ {2} ^ {2} = \ min _ {\ alfa} \ | A \ alfa -y \ | _ {2} ^ {2}}$

voidaan muotoilla tavallisissa tapauksissa (eli sillä on koko sarakkeen sijoitus , joten se on säännöllinen ja siten käänteinen) kaavalla ${\ displaystyle A}$${\ displaystyle A ^ {T} A}$

${\ displaystyle \ alpha = (A ^ {T} A) ^ {- 1} A ^ {T} y}$

voidaan ratkaista selkeästi analyyttisesti, kuten seuraavassa osassa selitetään. Kun yksittäinen tapaus, jos ei ole täysiasteinen järjestelmä normaaliyhtälöitä ei yksikäsitteisesti ratkaistavissa, i. H. parametria ei voida tunnistaa (katso Gauss-Markowin lause # Yksittäinen tapaus, arvioitavat funktiot ). ${\ displaystyle A}$${\ displaystyle \ alpha}$

Ratkaisu minimointiongelmaan

Johtaminen ja menettely

Minimointiongelma syntyy, kuten on esitetty yleisessä lineaarisessa tapauksessa, kuten

${\ displaystyle \ min _ {\ alpha} \ | A \ alpha -y \ | _ {2} ^ {2} = \ min _ {\ alpha} (A \ alpha -y) ^ {T} (A \ alpha -y) = \ min _ {\ alpha} (\ alpha ^ {T} A ^ {T} A \ alpha -2y ^ {T} A \ alpha + y ^ {T} y).}$

Tämä ongelma voidaan aina ratkaista. Jos matriisilla on täysi sijoitus , ratkaisu on jopa yksiselitteinen. Määrittää Esseenin piste, nollaus osittaisderivaatat suhteen , ${\ displaystyle A}$${\ displaystyle \ alpha _ {j}}$

${\ displaystyle \ nabla \ | A \ alpha -y \ | _ {2} ^ {2} = 2 (A \ alpha -y) ^ {T} A,}$

lineaarinen normaaliyhtälöjärjestelmä (myös Gaussin normaaliyhtälöt tai normaaliyhtälöt )

${\ displaystyle A ^ {T} A \ alpha = A ^ {T} y,}$

joka tarjoaa ratkaisun minimointitehtävään ja joka on yleensä ratkaistava numeerisesti. Sillä on täysi sijoitus ja se on , matriisi on positiivinen ja varma, joten löydetty ääripää on todellakin minimi. Tällä tavalla minimointitehtävän ratkaiseminen voidaan vähentää yhtälöjärjestelmän ratkaisemiseksi. Yksinkertaisesti parhaiten sopivan suoran tapauksessa sen ratkaisu voidaan, kuten on osoitettu, antaa jopa suoraan yksinkertaisena kaavana. ${\ displaystyle A}$${\ displaystyle n \ geq m}$${\ displaystyle A ^ {T} A}$

Vaihtoehtoisesti esityksessä voidaan käyttää normaaliyhtälöitä

${\ displaystyle A ^ {T} A \ alpha -A ^ {T} y = {\ begin {pmatrix} \ left \ langle \ varphi _ {1}, \ varphi _ {1} \ right \ rangle & \ left \ langle \ varphi _ {1}, \ varphi _ {2} \ right \ rangle & \ cdots & \ left \ langle \ varphi _ {1}, \ varphi _ {m} \ right \ rangle \\\ left \ langle \ varphi _ {2}, \ varphi _ {1} \ oikea \ rangle & \ vasen \ langle \ varphi _ {2}, \ varphi _ {2} \ oikea \ rangle & \ cdots & \ vasen \ langle \ varphi _ { 2}, \ varphi _ {m} \ oikea \ rangle \\\ vdots & \ vdots & \ ddots & \ vdots \\\ left \ langle \ varphi _ {m}, \ varphi _ {1} \ right \ rangle & \ left \ langle \ varphi _ {m}, \ varphi _ {2} \ right \ rangle & \ cdots & \ left \ langle \ varphi _ {m}, \ varphi _ {m} \ right \ rangle \\\ end {pmatrix}} {\ begin {pmatrix} \ alpha _ {1} \\\ alpha _ {2} \\\ vdots \\\ alpha _ {m} \ end {pmatrix}} - {\ begin {pmatrix} \ vasen \ langle y, \ varphi _ {1} \ oikea \ rangle \\\ vasen \ langle y, \ varphi _ {2} \ oikea \ rangle \\\ vdots \\\ vasen \ langle y, \ varphi _ {m } \ oikea \ rangle \\\ end {pmatrix}} = 0.}$

kirjoittaa, jolloin standardi skalaaritulo tuote symboloi ja voi myös ymmärrettävä integraali päällekkäisyys perustoiminnot. Perustoiminnot on luettava vektoreina, joissa on erilliset tukipisteet havaintojen sijainnissa . ${\ displaystyle \ left \ langle \ cdot, \ cdot \ right \ rangle}$${\ displaystyle \ varphi _ {i}}$${\ displaystyle {\ vec {\ varphi _ {i}}} = (\ varphi _ {i} (x_ {1,1}, \ pisteitä, x_ {N, 1}), \ varphi _ {i} (x_ {1,2}, \ pisteitä, x_ {N, 2}), \ pisteitä, \ varphi _ {i} (x_ {1, n}, \ pisteitä, x_ {N, n}))}$${\ displaystyle n}$${\ displaystyle y = {\ vec {y}} = (y_ {1}, y_ {2}, \ ldots, y_ {n})}$

Lisäksi minimointiongelma voidaan analysoida hyvin yksittäisen arvon hajoamisella . Tämä myös motivoi pseudo -käänteisen ilmaisemista, matriisin normaalin käänteisen yleistämistä . Tämä antaa sitten perspektiivin ei-neliömäisille lineaarisille yhtälöjärjestelmille, jotka mahdollistavat ei stokastisen, mutta algebrallisesti motivoituneen ratkaisukonseptin.

Liuoksen numeerinen käsittely

On kaksi tapaa ratkaista ongelma numeerisesti. Toisaalta normaalit yhtälöt

${\ displaystyle A ^ {T} A \ alpha = A ^ {T} y}$

jotka ovat ainutlaatuisesti ratkaistavissa, jos matriisilla on täysi sijoitus. Lisäksi tuotteen summa matriisin on ominaisuus, että positiivinen selvä , joten sen ominaisarvot ovat kaikki positiivisia. Yhdessä symmetrian kanssa tätä voidaan käyttää ongelman ratkaisemiseen käytettäessä numeerisia menetelmiä: esimerkiksi Cholesky -hajoamisella tai CG -menetelmällä . Koska matriisin kunto vaikuttaa voimakkaasti molempiin menetelmiin , tämä ei toisinaan ole suositeltava lähestymistapa: Jos ehto on jo huono, neliö on huonossa kunnossa. Tämän seurauksena pyöristysvirheitä voidaan vahvistaa siinä määrin, että ne tekevät tuloksesta käyttökelvottoman. Kuitenkin regularisointi menetelmiä voidaan tilan parantamiseksi. ${\ displaystyle A}$ ${\ displaystyle A ^ {T} A}$${\ displaystyle A ^ {T} A}$${\ displaystyle A}$${\ displaystyle A ^ {T} A}$

Yksi menetelmä on ns. Harjanteen regressio , joka ulottuu Hoerliin ja Kennardiin (1970). Englanninkielinen sana ridge tarkoittaa jotain, kuten harjun, riutta, takaisin. Huonosti ehdollistetun matriisin sijasta käytetään tässä paremmin ilmastoitua matriisia . Tässä on ulotteinen yksikkömatriisi. Taide on oikea valinta . Liian pieni lisää kestävyyttä vain vähän, liian suuri johtaa vääristyneeseen sopeutumiseen. ${\ displaystyle A ^ {T} A}$${\ displaystyle A ^ {T} A + \ delta I_ {m}}$${\ displaystyle I_ {m}}$${\ displaystyle m}$${\ displaystyle \ delta}$${\ displaystyle \ delta}$${\ displaystyle \ delta}$

Toisaalta alkuperäinen minimointitehtävä tarjoaa vakaamman vaihtoehdon, koska pienellä minimiarvolla sillä on ehto, jonka suuruusluokka on ehto , ja suuret neliön arvot . QR -hajoamista käytetään laskettaessa ratkaisu , joka syntyy kotitalouden muunnoksilla tai Givensin kierroksilla . Perusajatuksena on, että ortogonaaliset muunnokset eivät muuta vektorin euklidista normia. Niin on myös ${\ displaystyle A}$${\ displaystyle A}$

${\ displaystyle \ | A \ alpha -y \ | _ {2} = \ | Q (A \ alpha -y) \ | _ {2}}$

jokaiselle ortogonaaliselle matriisille . Ongelman ratkaisemiseksi voidaan laskea QR-hajoaminen , jolloin myös oikea puoli muutetaan suoraan. Tämä johtaa lomakkeeseen ${\ displaystyle Q}$${\ displaystyle A}$

${\ displaystyle \ | R \ alpha -Q ^ {T} y \ | _ {2}}$

kanssa , jossa on oikea ylempi kolmiomatriisin . Ratkaisu ongelmaan saadaan siten ratkaisemalla yhtälöjärjestelmä ${\ displaystyle R = {\ begin {pmatrix} {\ tilde {R}} \\ 0 \ end {pmatrix}},}$${\ displaystyle {\ tilde {R}} \ in \ mathbb {R} ^ {m \ times m}}$

${\ displaystyle {\ tilde {R}} {\ begin {pmatrix} \ alpha _ {1} \\\ vdots \\\ alpha _ {m} \ end {pmatrix}} = {\ begin {pmatrix} (Q ^) {T} y) _ {1} \\\ vdots \\ (Q ^ {T} y) _ {m} \ end {pmatrix}}.}$

Minimin normi johtuu sitten muunnetun oikean puolen jäljellä olevista komponenteista, koska niihin liittyvät yhtälöt eivät koskaan voi täyttyä nollaviivojen vuoksi . ${\ displaystyle (Qy) _ {m + 1}, \ pisteitä, (Qy) _ {n},}$${\ displaystyle R}$

Tilastollisten regressioanalyysi , koska useita muuttujia, puhutaan ja moninkertaisen lineaarisen regression . Yleisin lähestymistapa, moninkertainen lineaarinen malli arvioitavaksi kuin tavallinen pienimmän neliösumman estimaatti tai tavallinen pienin neliö ( englanti tavallinen pienin neliö , lyhyesti OLS ). Toisin kuin tavallinen pienimmän neliösumman menetelmä on yleistetty pienimmän neliösumman menetelmä , käytetään lyhyttä VMKQ: ta ( englanninkielinen yleistetty vähimmäisneliö , lyhyesti GLS ) yleistetyssä lineaarisessa regressiomallissa . Tässä mallissa virhetermit poikkeavat jakauman oletuksesta, kuten epäkorrelaatio ja / tai homoskedastisuus . Sitä vastoin monimuuttujaisella regressiolla on jokaiselle havainnolle monia arvoja, joten vektorin sijasta on matriisi (katso yleinen lineaarinen malli ). Lineaarisia regressiomalleja on tiiviisti tutkittu todennäköisyysteorian kannalta. Erityisesti ekonometriassa analysoidaan esimerkiksi monimutkaisia rekursiivisesti määriteltyjä lineaarisia rakenneyhtälöitä talousjärjestelmien mallintamiseksi. ${\ displaystyle x_ {1}, \ ldots, x_ {n}}$ ${\ displaystyle i}$ ${\ displaystyle (i = 1, \ pisteitä, n)}$ ${\ displaystyle r}$${\ displaystyle y}$${\ displaystyle n \ kertaa r}$${\ displaystyle Y}$

Rajoitusongelmat

Parametreista tiedetään usein lisätietoja, jotka muotoillaan toissijaisissa olosuhteissa, jotka ovat sitten saatavilla yhtälöiden tai eriarvoisuuksien muodossa. Yhtälöt näkyvät esimerkiksi silloin, kun tietyt datapisteet on interpoloitava. Eriarvoisuuksia esiintyy useammin, yleensä yksittäisten parametrien aikaväleinä. Jousivakio mainittiin johdanto -esimerkissä; se on aina suurempi kuin nolla ja se voidaan aina arvioida ylöspäin tarkasteltavana olevassa tapauksessa.

Yhtälön tapauksessa näitä voidaan käyttää kohtuullisen ongelman ratkaisemiseksi, jotta alkuperäinen minimointitehtävä muutettaisiin alemmaksi ulottuvuudeksi, jonka ratkaisu täyttää automaattisesti rajoitukset.

Eriarvoisuus on vaikeampaa. Ongelma syntyy tässä lineaarisessa epätasa -arvossa

${\ displaystyle \ min _ {\ alpha} \ | {\ vec {f}} - {\ vec {y}} \ | _ {2} \;}$kanssa ,${\ displaystyle \; l \ leq C \ alpha \ leq u}$${\ displaystyle C \ \ mathbb {R} ^ {n \ times n},}$

jossa eriarvoisuus on tarkoitettu komponenttikohtaisesti. Tämä ongelma voidaan ratkaista ainutlaatuisesti kuperaksi ja toisen asteen optimointitehtäväksi, ja sitä voidaan käsitellä esimerkiksi menetelmillä tällaisten ongelmien ratkaisemiseksi.

Asteen epätasa syntyy esimerkiksi, kun käytetään Tychonow regularisointi ratkaista kiinteä yhtälöt . Ratkaisukykyä ei aina anneta tässä. Numeerinen ratkaisu voi tapahtua esimerkiksi erityisillä QR -hajoamisilla .

Epälineaariset mallitoiminnot

Perusidea ja menettelytapa

Tehokkaiden tietokoneiden myötä erityisesti epälineaarisen regression merkitys kasvaa. Parametrit sisältyvät funktioon epälineaarisesti. Epälineaarinen mallinnus mahdollistaa periaatteessa tietojen sovittamisen mihin tahansa muotoyhtälöön . Koska nämä yhtälöt määrittävät käyrät , termejä epälineaarinen regressio ja "käyrän sovitus" käytetään enimmäkseen synonyymeinä. ${\ displaystyle y = f (\ alpha)}$

Jotkut epälineaariset ongelmat voidaan muuntaa lineaarisiksi sopivalla korvaamisella ja ratkaista sitten kuten edellä. Lomakkeen moninkertainen malli

${\ displaystyle y = \ alpha _ {0} \ cdot x ^ {\ alpha _ {1}}}$

voidaan muuntaa lisäsysteemiksi käyttämällä esimerkiksi logaritmia . Tätä lähestymistapaa käytetään muun muassa kasvuteoriassa .

Yleensä epälineaaristen mallitoimintojen kanssa syntyy muotoongelma

${\ displaystyle \ min _ {\ alpha} \ | f (\ alpha) -y \ | _ {2},}$

epälineaarisella toiminnolla . Osittainen erilaistuminen johtaa tällöin normaalien yhtälöiden järjestelmään, jota ei voida enää ratkaista analyyttisesti. Numeerinen ratkaisu voidaan tehdä iteratiivisesti Gauss-Newtonin menetelmällä . ${\ displaystyle f}$

Nykyiset ohjelmat toimivat usein yhdellä variantilla, Levenberg-Marquardt-algoritmilla . Tässä on regularisointi yksitoikkoisuus likimääräisen tuloksen taattu. Lisäksi menetelmä on suvaitsevaisempi kuin alkuperäinen menetelmä, jos arvioiduissa arvoissa on suurempi poikkeama. Molemmat menetelmät liittyvät Newtonin menetelmään ja sopivissa olosuhteissa (lähtökohta on riittävän lähellä paikallista optimumia) yleensä lähentyvät neliömäisesti , eli oikeiden desimaalien määrä kaksinkertaistuu jokaisessa vaiheessa.

Jos eriyttäminen on tavoitefunktion monimutkaisuuden vuoksi liian aikaa vievää, vaihtoehtoisia ratkaisuja on saatavana useita muita menetelmiä, jotka eivät vaadi johdannaisia, katso paikallisen epälineaarisen optimoinnin menetelmät .

Esimerkki ei-linearisoituvan mallitoiminnon entsyymikinetiikasta

Esimerkki täysin epälineaarisista regressiomalleista on entsyymien kinetiikka . Tässä vaaditaan, että "vain" (reaktionopeus) eikä (substraatin konsentraatio) altistuu virheelle ja sitä voidaan siten käyttää muuttujana. Lineweaver-Burk-suhde on algebrallisesti oikea transformaatio Michaelis-Menten yhtälö , mutta sen soveltaminen tarjoaa vain oikeat tulokset, jos mitatut arvot ovat virheettömiä. Tämä johtuu siitä, että todellisuus syntyy vain Michaelis-Menten-suhteen laajentuessa ${\ displaystyle y}$${\ displaystyle \ alpha}$${\ displaystyle \ alpha}$ ${\ displaystyle v = V _ {\ mathrm {max}} \ cdot [S] / (K_ {m} + [S])}$

${\ displaystyle \ nu _ {i} = {\ frac {V _ {\ max} \ vasen [S_ {i} \ oikea]} {K_ {m} + \ vasen [S_ {i} \ oikea]}} ( 1 + e_ {i}) \ {\ boldsymboli {\ nu}} _ {i}}$

voidaan kuvata kanssa , koska virhe parametri. Tätä yhtälöä ei voi enää linearisoida, joten ratkaisu on määritettävä täällä iteratiivisesti. ${\ displaystyle e_ {i}}$

Väärinkäytöksiä, jos vaatimukset eivät täyty

Pienimmän neliösumman menetelmä mahdollistaa tietyissä olosuhteissa kaikkien malliparametrien todennäköisimmän laskemisen. Tätä varten on oltava valittu oikea malli, oltava riittävästi mitattuja arvoja ja mitattujen arvojen poikkeamat mallijärjestelmästä muodostavat normaalijakauman . Käytännössä menetelmää voidaan kuitenkin käyttää myös eri tarkoituksiin, jos nämä vaatimukset eivät täyty. On kuitenkin huomattava, että pienimmän neliösumman menetelmä voi antaa täysin ei -toivottuja tuloksia tietyissä epäsuotuisissa olosuhteissa. Esimerkiksi mitatuissa arvoissa ei saa olla poikkeamia , koska ne vääristävät arvioinnin tulosta . Lisäksi arvioitavien parametrien välinen monikollineaarisuus on epäedullinen, koska se aiheuttaa numeerisia ongelmia. Muuten, regressorit, jotka ovat kaukana muista, voivat myös vaikuttaa voimakkaasti oikaisulaskelman tuloksiin. Tässä puhutaan arvoista, joilla on suuri vipuvaikutus ( englantilainen korkea vipuvaikutus ).

Monikollineaarisuus

Ilmiö multikollineaarisuus syntyy, kun mittauksia kahden annetun muuttujia ja erittäin korkea korrelaatio on niin on lähes lineaarisesti riippuvainen. Lineaarisen tapauksessa tämä tarkoittaa sitä, että determinantti normaaliyhtälön matriisi on hyvin pieni, ja päinvastoin, normi käänteinen on erittäin suuri; ehto on täten merkittävästi alentunut. Normaaliyhtälöitä on silloin vaikea ratkaista numeerisesti. Ratkaisuarvot voivat tulla uskomattoman suuria, ja pienetkin muutokset havainnoissa aiheuttavat suuria muutoksia arvioihin. ${\ displaystyle x_ {i}}$${\ displaystyle x_ {j}}$${\ displaystyle A ^ {T} A}$${\ displaystyle A ^ {T} A}$

Juokse pois

Data-arvoja ”eivät sovi Mittaussarjan” määritellään kuten harha . Nämä arvot vaikuttavat voimakkaasti parametrien laskentaan ja väärentävät tuloksen. Tämän välttämiseksi tiedot on tutkittava virheellisten havaintojen varalta. Havaitut poikkeamat voidaan poistaa esimerkiksi mittaussarjasta tai käyttää vaihtoehtoisia poikkeamia kestäviä laskentamenetelmiä, kuten painotettua regressiota tai kolmen ryhmän menetelmää.

Ensimmäisessä tapauksessa arvioitujen arvojen ensimmäisen laskemisen jälkeen tilastollisilla testeillä tarkistetaan, onko yksittäisissä mittausarvoissa poikkeamia. Nämä mitatut arvot hylätään ja arvioidut arvot lasketaan uudelleen. Tämä menetelmä sopii, kun poikkeamia on vain muutama.

Painotetussa regressiossa riippuvat muuttujat painotetaan niiden jäännösten mukaan . Poikkeamat, d. H. Havainnoilla, joissa on suuria jäännöksiä, on pieni paino, joka voidaan luokitella jäännöksen koon mukaan. Mostellerin ja Tukeyn (1977) mukaan algoritmissa , jota kutsutaan biopainotukseksi, ongelmattomat arvot painotetaan 1: llä ja outliers 0: lla, mikä tarkoittaa, että outlier poistetaan. Painotetulla regressiolla tarvitaan yleensä useita iterointivaiheita, kunnes tunnistettujen poikkeamien joukko ei enää muutu. ${\ displaystyle y}$

Yleistetyt vähimmän neliön mallit

Jos virhetermejä koskevassa menettelyssä asetetut tiukat vaatimukset pehmennetään, saadaan ns. Yleistettyjä pienimmän neliösumman lähestymistapoja . Tärkeillä erityistapauksilla on tällöin omat nimensä, kuten painotetut pienimmät neliöt ( englanninkieliset painotetut pienimmät neliöt , lyhyesti WLS ), joissa virheiden oletetaan edelleen olevan korreloimattomia, mutta eivät enempää samaa varianssia. Tämä johtaa muotoongelmaan

${\ displaystyle \ | D (A \ alpha -y) \ | _ {2},}$

jossa D on diagonaalinen matriisi . Jos varianssit vaihtelevat suuresti, vastaavilla normaaliyhtälöillä on erittäin suuri tila , minkä vuoksi ongelma on ratkaistava suoraan.

Jos oletetaan lisäksi, että mittausdatan virheet tulee ottaa huomioon myös mallitoiminnossa, tuloksena on lomakkeen "pienimmät neliöt yhteensä"

${\ displaystyle \ min _ {E, r} \ | (E, r) \ | _ {F}, (A + E) \ alpha = b + r,}$

missä virhe on mallissa ja virhe tiedoissa.${\ displaystyle E}$${\ displaystyle r}$

Lopuksi on myös mahdollisuus olla käyttämättä perusjakaumaa normaalijakaumana. Tämä vastaa esimerkiksi minimointia ei Euklidisen normissa, vaan summa -normissa . Tällaiset mallit ovat regressioanalyysin kohteita .

Osittainen vähiten neliöiden regressio (PLS)

Osittainen pienimmän neliösumman regressio (englantilainen Partial Least Squares, PLS) tai "projektio piilevään rakenteeseen" on monimuuttujainen menetelmä, ja sitä voidaan käyttää ulottuvuuden pienentämiseen, jolloin pääkomponentin regression tapaan tulon muunnos ja kohdemuuttujat tapahtuvat.

kirjallisuus

• Åke Björck: Numeeriset menetelmät pienimpien neliöiden ongelmille. SIAM, Philadelphia 1996, ISBN 0-89871-360-9 .
• Walter Großmann: Tasoituslaskennan perusteet. 3. laaj. Painos. Springer Verlag, Berliini / Heidelberg / New York 1969, ISBN 3-540-04495-7 .
• Richard J. Hanson, Charles L. Lawson: Pienimmän neliön tehtävien ratkaiseminen. SIAM, Philadelphia 1995, ISBN 0-89871-356-0 .
• Frederick Mosteller , John W. Tukey : Data Analysis and Regression - toinen kurssi tilastoissa. Addison-Wesley, Reading MA 1977, ISBN 0-201-04854-X .
• Gerhard Sacrifice: Numeerinen matematiikka aloittelijoille. Johdanto matemaatikoille, insinööreille ja tietojenkäsittelytieteilijöille. 4. painos. Vieweg, Braunschweig 2002, ISBN 3-528-37265-6 .
• Peter Schönfeld: Ekonometrian menetelmät. 2 osaa. Vahlen, Berliini / Frankfurt 1969–1971.
• Eberhard Zeidler (toim.): Matematiikan taskukirja. Perusteltu v. IN Bronstein, KA Semendjajew. Teubner, Stuttgart / Leipzig / Wiesbaden 2003, ISBN 3-8171-2005-2 .
• T. Strutz: Tietojen sovittaminen ja epävarmuus (Käytännöllinen johdanto painotettuihin pienimpiin neliöihin ja sen jälkeen). 2. painos. Springer Vieweg, 2016, ISBN 978-3-658-11455-8 .

nettilinkit

Yksilöllisiä todisteita

1. ↑ Göttingen. Julkaisussa:  Goettingische -mainokset opituista asioista / Goettingische -mainokset oppituista asioista / Goettingische -oppineet mainokset , 23. tammikuuta 1802, s. 1 (verkossa ANNOssa ).Malli: ANNO / huolto / kaasu
2. ^ Moritz Cantor :  Gauß: Karl Friedrich G. julkaisussa: Allgemeine Deutsche Biographie (ADB). Vuosikerta 8, Duncker & Humblot, Leipzig 1878, s. 430-445., Tässä s.436.
3. ↑ Paul Karlson: Numeroiden taika. Ullstein-Verlag, Berliini-Länsi. Yhdeksäs, tarkistettu ja laajennettu painos, 1967, s.
4. ^ A. Abdulle, Gerhard Wanner : 200 vuotta pienimmän neliön menetelmiä . Julkaisussa: Elements of Mathematics , Volume 57, 2002, s.45-60 , doi: 10.1007 / PL00000559 .
5. ↑ Vrt. Moritz Cantor :  Gauß: Karl Friedrich G. julkaisussa: Allgemeine Deutsche Biographie (ADB). Osa 8, Duncker & Humblot, Leipzig 1878, s. 430-445., S.436.
6. ^ Adrien-Marie Legendre: Nouvelles méthodes pour la détermination des orbites des comètes. Pariisi 1805, s. 72–80 (liite): Sur la Méthode des moindres quarrés.
7. ^ Carl Friedrich Gauß: Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium . Göttingen 1809; Carl Haase (käänn.): Teoria taivaankappaleiden liikkeestä, jotka kiertävät aurinkoa kartiomaisissa osissa. Hannover 1865.
8. ^ Matriisit ja determinantit .
9. ↑ Painettu julkaisussa Gauß, Werke, Volume X / 1, s.380.
10. ↑ Abdulle, Wanner: Matematiikan elementit . Vuosikerta 57, 2002, s. 51. Päiväkirjamerkinnän faksikopio.
11. ^ Laplace, lainattu Herman Goldstine: Numeerisen analyysin historia . Springer, 1977, s.209.
12. ^ Carl Friedrich Gauß: Theoria Combinationis observum erroribus minimis obnoxiae. 2 osaa. Göttingen 1821–1823 (Commentationes Societatis Regiae Scientiarum Gottingensis recentiores, classis mathematicae, osa 5); Täydentävä Theoria -yhdistelmä on havaintovirhevirhe, joka on minimis obnoxiae. Göttingen 1826/28 (Commentationes Societatis Regiae Scientiarum Gottingensis recentiores, classis mathematicae, nide 6.). Anton Börsch Paul Simon (Toim.): Carl Friedrich Gaussin traktaatit pienimmän neliösumman menetelmästä. Saksan kielellä. Berliini 1887, Textarchiv - Internet -arkisto .
13. ↑ Pete Stewart: Ehkä meidän pitäisi kutsua sitä ”Lagrangin eliminaatioksi” . NA Digest sunnuntai, 21. kesäkuuta 1991, 30. kesäkuuta 1991, osa 91, numero 26.
14. ↑ H.Wirths: Suhteellinen matematiikka regressiossa ja korrelaatiossa . Julkaisussa: Stochastik in der Schule , 1991, numero 1, s. 34–53
15. ↑ Hans R. Schwarz, Norbert Köckler: Numeerinen matematiikka. 7. tarkistettu Painos. Teubner, 2009, doi: 10.1007 / 978-3-8348-9282-9 , ISBN 978-3-8348-9282-9 , s.141 , luku 3.6 (Gaussin likimääräisyys), lause 3.23.
16. ↑ AE Hoerl ja RW Kennard: Ridge-regressio: puolueellinen arvio ei-ortogonaalisille ongelmille , Techno Metrics 12 (1970), 55-82.
17. ^ Sabine Van Huffel, Joos Vandewalle: Vähimmäisneliöiden kokonaisongelma: laskennalliset näkökohdat ja analyysi. SIAM-julkaisut, Philadelphia PA 1991, ISBN 0-89871-275-0 .
18. ↑ Martin Plesinger: Vähimmäisneliöiden kokonaisongelma ja tietojen vähentäminen AX: ssä ≈ B. Väitöskirja. ( Muisto 24. heinäkuuta 2012 Internet -arkistossa ; PDF; 1,6 Mt) TU Liberec ja ICS Prague, 2008.
19. ↑ Osittainen vähiten neliöiden regressio. 3. elokuuta 2017, katsottu 23. elokuuta 2021 (saksa). 
20. ↑ 1.8. Ristien hajoaminen - Scikit -Learn 0.24.2 -dokumentaatio. Haettu 23. elokuuta 2021 .