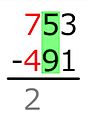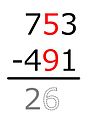vähennyslasku

Vähennys (ja lat. Subtrahere "pull", "poista"), puhekielessä miinus laskelma kutsutaan, on yksi neljästä peruslaskutoimitusta of aritmeettinen . Alle vähennyslasku tarkoitetaan poistamista on useita toisen. Matemaattisesti vähennyslasku on kaksinumeroinen yhdistelmä . Vähennyslaskun on käänteinen lisäys . Aritmeettinen symboli varten vähennys on miinusmerkki "-".

Kielisäännöt, perusominaisuudet ja merkinnät

Seuraavia symboleja ja puhetapoja käytetään vähennyselementteihin:

• Vähennyksen aritmeettinen symboli on miinusmerkki "-". Sen esitteli Johannes Widmann vuonna 1489 .
• Numeroa, josta jokin vähennetään, kutsutaan minuendiksi (latinankielinen "pienennettävä").
• Numeroa, joka vähennetään, kutsutaan subtrahendiksi (latinaksi "omavastuu").
• Aritmeettinen lauseke ( termi ), joka sisältää minuend, miinusmerkki ja vähentäjä kutsutaan eroa .
• Vähennyksen tulos on eron arvo (myös eron arvo tai vain ero ).
• Erojen symboli termeinä on Kreikan iso kirjain delta "Δ", jota käytetään myös operaattorina erojen muodostuksessa (katso alla). Usein ero - etenkin jokapäiväisessä käytössä - on vain seurausta tämän "miinus laskenta", ja useammin määrää tämän tuloksen. Esimerkki: Ero välillä 7 ja 9 ja ero välillä 5 on 2 . Esimerkissä tätä korostetaan verbillä "summat".

Muistisääntö: minuend miinus vähentäjä samanarvoisuutta erotuksen ( muistisääntö : M inuend tulee aakkosissa ennen S ubtrahend)

Esimerkkejä (ottaen huomioon merkki!):

• 4 miinus 1 kirjoitetaan (sama) 3 tai eri tavalla .${\ displaystyle 4-1 = 3}$

4 on minuend, 1 on subtrahend, aritmeettinen lauseke (termi) on ero ja tulos 3 on eron tai eron arvo. ${\ displaystyle 4-1}$

Joukko luonnollisia lukuja ei ole täydellinen osalta vähennys , joka on, jossa vähennys yksi mahdollisesti saavuttaa tulos, joka ylittää alueella luonnollisia lukuja .

• Esimerkki: ${\ displaystyle 1-4 = -3}$

On olemassa lyhennettyjä merkintöjä esimerkiksi tai: lle , jota käytetään pääasiassa termeihin kuten tai . ${\ displaystyle alkaen}$${\ displaystyle x | _ {x = b} ^ {x = a}}$${\ displaystyle [x] _ {b} ^ {a}}$${\ displaystyle f (a) -f (b) = f (x) | _ {x = b} ^ {x = a}}$${\ displaystyle F (a) -F (b) = [F (x)] _ {b} ^ {a} = [F (x)] _ {x = b} ^ {x = a} = F (x) ) {\ Iso |} _ {b} ^ {a} = F (x) {\ Iso |} _ {x = b} ^ {x = a}}$

Jos useita vähennyksiä tapahtuu peräkkäin, lauseketta käsitellään vasemmalta oikealle; vähennyslasku on siis vasemmalle assosiatiivista :

• ${\ displaystyle abc = (ab) -c}$.

Matemaattinen määritelmä

Vähennyslaskun on käänteinen lisäys . Vuonna ryhmissä te löytyy tasan kunkin annetun ja siten, että: ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle x}$

${\ displaystyle b + x = a \!}$

Määrittämistä kutsutaan vähennykseksi . voidaan määrittää mukaan vähentämällä alkaen : ${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle b}$${\ displaystyle a}$

${\ displaystyle x = lähettäjä}$

${\ displaystyle a}$kutsutaan minuend , vähentäjä . Vähennyksen tulosta kutsutaan tässä eron arvoksi . Vähennys merkitään miinusmerkillä: ${\ displaystyle b}$${\ displaystyle x}$

${\ displaystyle alkaen}$

Vähennyslaskun voidaan myös määritellä lisäämällä vastapäätä määrä vähentäjä on minuend : ${\ displaystyle alkaen}$ ${\ displaystyle -b = (- 1) \ cdot b}$${\ displaystyle a}$

${\ displaystyle ab = a + (- 1) \ cdot b = a + (- b)}$

Perusmenettely

Graafinen menetelmä

Graafisessa menetelmässä numeeriset arvot esitetään palkoina, viivoina, pisteinä tai muina abstrakteina esineinä. Toinen mahdollisuus on esitys vektoreilla , jolloin alaliittovektorin suunta käännetään päinvastaiseksi ja vektorit lasketaan yhteen.

esimerkki

•

•

•

•

•

•

•

•

•

•

•

•

•

(13)

-

•

•

•

•

•

•

•

•

•

(9)

=

•

•

•

•

(4)

Vähennys-vähennysmenetelmä

Kun vähennys vähennyksen menetelmä , osittainen määrä vähentäjä vähennetään vähentäjä ja minuend kunnes vähentäjä on 0. Kymmenet valitaan yleensä välivaiheeksi.

esimerkki

${\ displaystyle 13-9 = (13-3) - (9-3) = 10-6 = 4}$

Vähennyslaskumenetelmä

Kun vähennys-lisäys menetelmä , vähentäjän ja minuend jaetaan osakomponenttien, vähennetään näitä, ja sitten osittainen määrät lisätään uudelleen.

esimerkki

${\ displaystyle 13-9 = (10 + 3) -9 = (10-9) + 3 = 1 + 3 = 4}$

Täydennysmenetelmä

Kun täydennys menetelmä , vastaava komplementti on laskettu pois vähentäjä . Sitten lisätään minuend ja subtraimen komplementti. Menetelmä on erityisesti teknisessä tietojenkäsittelytieteessä , kuten mekaanisessa kentässä Tarrant- Comptometer , mekaanista Hoffritz-summainta ja elektronisia lisäaineita voidaan käyttää nykyaikaisissa tietokonejärjestelmissä.

esimerkki

Aloituskaava:

${\ displaystyle 13_ {10} -9_ {10} = 1101_ {2} -1001_ {2}}$

Tämä sopii:

${\ displaystyle 13_ {10} + \ vasen (-9_ {10} \ oikea) = 1101_ {2} + \ vasen (-1001_ {2} \ oikea)}$

Komplementin laskeminen:

Komplementin laskeminen

leikkaus	Tuloksen arvo
	Kymmenet täydentävät	Kaksi täydentää
Lähtötaso	${\ displaystyle \ ldots \ 000 \ 009,0_ {10}}$	${\ displaystyle \ ldots \ 0000 \ 1001,0_ {2}}$
Inversio	${\ displaystyle \ ldots \ 999 \ 990, {\ piste {9}} _ {10}}$	${\ displaystyle \ ldots \ 1111 \ 0110, {\ piste {1}} _ {2}}$
Kanssa ${\ displaystyle 0, {\ dot {9}} _ {10} = 0, {\ dot {1}} _ {2} = 1}$	${\ displaystyle \ ldots \ 999 \ 991,0_ {10}}$	${\ displaystyle \ ldots \ 1111 \ 0111,0_ {2}}$

Lisäys:

${\ displaystyle {\ begin {array} {rrrcrrr} & 13_ {10} &&& 1101_ {2} \\ + & \ ldots \ 999 \ 991_ {10} && + & \ ldots \ 1111 \ 0111_ {2} \\ = = & 4_ {10} && = & 100_ {2} \ end {array}}}$

Kirjallinen vähennyslasku

Kirjallisen lisäyksen lisäksi kirjallinen vähennyslasku on yksi kulttuurin perusmenetelmistä, joka opitaan peruskoulun ensimmäisinä vuosina. Kirjallisen vähennyksen hallinta on edellytys kirjallisen jaon oppimiselle .

Pystysuuntainen vähennyslasku kuljettaa yli

Peruskouluissa tänään, päätetään yleensä opetetaan, jossa vastaava kannat minuend ja vähentäjä ovat päällä päällekkäin muiden. Asemia käsitellään peräkkäin, enimmäkseen oikealta vasemmalle.

Kirjallista vähennystä varten minuendin (numero yllä) on oltava suurempi tai yhtä suuri kuin alaliitto (numero (t) alla). Negatiiviset tulokset eivät siten ole mahdollisia suoraan.

Jos minuend on pienempi kuin alaliitto, merkit voidaan vaihtaa laskutoimitusta varten. Subtrahendista tulee minuend (kirjoitettu yllä) ja minuendistä tulee subtrahend (kirjoitettu alla). Seuraavassa kuvattua menettelyä voidaan käyttää laskennassa. Loppujen lopuksi tulos on kuitenkin annettava miinuksella, koska se on aina negatiivinen (ei luonnollinen luku). Tämä kääntää aikaisemmin laskutoimituksessa suoritetun muutoksen merkissä.

Jos alaliittymän numero on suurempi kuin samat paikat, käsitellään minunendin tarvitsemat siirrot . Toisin sanoen minuendea lisätään 10: llä vähennyksen mahdollistamiseksi; Tämän kompensoimiseksi joko minipistettä on vähennettävä vasemmanpuoleisessa sarakkeessa (eriyttämismenettely; siirtojen ennakkolaskenta) tai lisättyä (lisämenettely; vähennys oikealta vasemmalle). Saksankielisellä alueella jälkimmäinen lähestymistapa on vallinnut täydentävän menettelyn kanssa. Vuonna 2000 eräissä osavaltioissa tuli voimaan uusi opetussuunnitelma, joka nyt määrittelee eriyttämisen standardiksi sen täydentämisen sijaan.

Täydentävä menettely

Lisämenetelmällä, jota kutsutaan myös täyttötekniikaksi tai (Yhdysvalloissa) itävaltalaiseksi menetelmäksi ("Itävallan menetelmä"), vähennystä ei tehdä, mutta osa-arvoa lisätään minuutin loppuun saakka . Jos tämä ei ole mahdollista, minuend korotetaan 10: llä. Kymmentä ei ole "lainattu", vaan se lisätään 1: nä seuraavan osalaskelman vähennykseen. Saksankielisissä maissa tätä menettelytapaa opetetaan perusmenetelmänä peruskouluissa. Yksi menetelmän eduista on se, että se valmistelee sellaisten tehtävien käsittelyä, joissa minuendista on vähennettävä useita alitunnistuksia.

esimerkki

	kuvaus
${\ displaystyle {\ begin {array} {r} 75 {\ color {red} 3} \\ - {\ underderset {} {4}} 9 {\ color {red} 1} \\\ hline \ end {array }}}$	1 +… = 3
${\ displaystyle {\ begin {array} {r} 7 {\ color {red} 5} 3 \\ - {\ alaviivat {} {4}} {\ color {red} 9} 1 \\ hline {\ color {Harmaa} 2} \ loppu {matriisi}}}$	Tulos kirjoitetaan rivin alle.
${\ displaystyle {\ begin {array} {r} 7 {\ color {red} 5} 3 \\ - {\ alaviivat {} {4}} {\ color {red} 9} 1 \\ hline {\ color {Harmaa} 2} \ loppu {matriisi}}}$	9 +… = 5 Kohdistettu summa (5) on liian pieni!
${\ displaystyle {\ begin {array} {r} 7 {\ color {red} 5} 3 \\ - {\ underderset {\ color {red} 1} {4}} {\ color {red} 9} 1 \ \\ hline {\ color {Gray} 2} \ end {array}}}$	Siksi sitä korotetaan 10: llä. 1 on kirjoitettu seuraavan alitunnistuksen alle.
${\ displaystyle {\ begin {array} {r} 7 {\ color {red} 5} 3 \\ - {\ underderset {\ color {red} 1} {4}} {\ color {red} 9} 1 \ \\ hline {\ color {Gray} 62} \ end {array}}}$	9 +… = 15 Laskenta voidaan nyt suorittaa, tulos kirjoitetaan rivin alle.
${\ displaystyle {\ begin {array} {r} {\ color {red} 7} 53 \\ - {\ color {red} {\ underderset {1} {4}}} 91 \\\ hline {\ color { Harmaa} 62} \ end {array}}}$	(4 + 1) +… = 7
${\ displaystyle {\ begin {array} {r} {\ color {red} 7} 53 \\ - {\ color {red} {\ underderset {1} {4}}} 91 \\\ hline {\ color { Harmaa} 262} \ end {array}}}$	Tulos kirjoitetaan rivin alle.
${\ displaystyle {\ begin {array} {r} 753 \\ - {\ alaviivat {1} {4}} 91 \\\ hline {\ color {Gray} 262} \ end {array}}}$	Kokonaistulos.

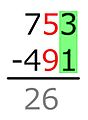
Vähennys vasemmalta oikealle

Vähennys voidaan suorittaa myös vasemmalta oikealle. Tässä epätavallisessa menettelyssä, joka on muunnos täydentävästä menettelystä, siirrot käsitellään ennen kuin ero lasketaan tarkasti. Koska siirtoja ei tarvitse huomata eikä muistaa, menetelmä on paitsi suhteellisen kestävä huolimattomille virheille, myös erittäin nopea ja jopa sopiva henkiseen aritmeettiseen.

esimerkki

• 

  7 - 4 = 3
  Tämä arvo ilmoitetaan vain, ei huomioida.

• 

  Koska seuraavan sarakkeen minuend on pienempi kuin alikäyttö, juuri laskettua arvoa vähennetään yhdellä.

• 

  15 - 9 = 6

• 

  Koska seuraavassa sarakkeessa oleva myyntiluku ei ole pienempi kuin alaliitto, tämä arvo säilyy.

• 

  3 - 1 = 2

Jos on sarake tai useita sarakkeita, joista löytyy kaksi samanlaista numeroa, ja sen oikealla puolella oleva sarake, jonka minipiste on pienempi kuin aliyhteys, tässä prosessissa käytetty rutiininomainen "ennakointi" ei vain samat kaksi numeroa, mutta myös seuraavat sarakkeet. Jokainen sarake, jolla on samat numerot, saa tuloksena yhdeksän nollan sijasta.

Ennuste useissa sarakkeissa edellä kuvatuissa tapauksissa on tämän menetelmän heikko kohta.

Eriyttämismenettely

Peruutus "eriyttämisellä" tarkoittaa, että liian pieni Minuend tekee "lainaa" vasemman naapurinsa kanssa. Minun loppua korotetaan 10: llä ja vasenta naapuria vähennetään 1: llä. Prosessia käytetään esimerkiksi peruskouluissa. B. opetti Yhdysvalloissa normaalina käytäntönä. Pelkkä laskentaprosessi on samanlainen kuin lisämenettelyssä; kuitenkin, jos nolla on "lainattava", sen on "lainattava" omalta vasemmalta naapuriltaan - tekniikka, joka on opittava lisäksi (sitä ei tarvita täydentävässä menettelyssä). Lisäksi eriyttämistä varten on kirjoitettava enemmän.

esimerkki

	kuvaus
${\ displaystyle {\ begin {array} {r} 75 {\ color {red} 3} \\ - 49 {\ color {red} 1} \\\ hline \ end {array}}}$	3 - 1 = ...
${\ displaystyle {\ begin {array} {r} 75 {\ color {red} 3} \\ - 49 {\ color {red} 1} \\\ hline {\ color {Gray} 2} \ end {array} }}$	Tulos kirjoitetaan rivin alle.
${\ displaystyle {\ begin {array} {r} 7 {\ color {red} 5} 3 \\ - 4 {\ color {red} 9} 1 \\\ hline {\ color {Gray} 2} \ end { taulukko}}}$	5 - 9 =… Minuend (5) on liian pieni!
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Grey} 6} {\ peruuta {7}}} {\ overset {\ color {punainen} 15} {\ peruuta {5}}} 3 \\ - 4 {\ color {red} 9} 1 \\\ hline {\ color {Gray} 2} \ end {array}}}$	Siksi sitä korotetaan 10: llä. Tämä 10 on "lainattu" vasemmalla olevasta numerosta (7); tätä vähennetään yhdellä.
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Grey} 6} {\ peruuta {7}}} {\ overset {\ color {punainen} 15} {\ peruuta {5}}} 3 \\ - 4 {\ color {red} 9} 1 \\\ hline {\ color {Gray} 62} \ end {array}}}$	15 - 9 =… Vähennys voidaan nyt suorittaa. Tulos kirjoitetaan rivin alle.
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Red} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ Cancel {5}}} 3 \\ - {\ color {red} 4} 91 \\\ hline {\ color {Gray} 62} \ end {array}}}$	6 - 4 = ...
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Red} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ Cancel {5}}} 3 \\ - {\ color {red} 4} 91 \\\ hline {\ color {Gray} 262} \ end {array}}}$	Tulos kirjoitetaan rivin alle.
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Grey} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ Cancel {5}}} 3 \\ - 491 \\\ hline {\ color {Gray} 262} \ end {array}}}$	Kokonaistulos.

Eriyttäminen

Erotteluprosessin muunnelma on, että kaikki pisteet erotetaan kokonaan ensimmäisessä työvaiheessa siten, että toiseen työvaiheeseen, jossa tehdään vain vähennys, on käytettävissä riittävän suuria minipisteitä.

esimerkki

	kuvaus
${\ displaystyle {\ begin {array} {r} 75 {\ color {red} 3} \\ - 49 {\ color {red} 1} \\\ hline \ end {array}}}$	3 - 1 = mahdollista. Ei "lainata" vasemmalta olevasta numerosta ei ole tarpeen.
${\ textstyle {\ begin {array} {r} {\ overset {\ color {Gray} 6} {\ cancel {7}}} {\ overset {\ color {Grey} 15} {\ cancel {\ color {punainen } 5}}} 3 \\ - 4 {\ color {red} 9} 1 \\\ hline \ end {array}}}$	5 - 9 = ei mahdollista. 5 lisätään 10: llä. Koska 10 on "lainattu" vasemmalla olevasta 7: stä, sitä on vähennettävä yhdellä.
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Grey} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ Cancel {5}}} {\ color {red} 3} \\ - 49 {\ color {red} 1} \\\ hline {\ color {Gray} 2} \ end {array}}}$	Numeroiden käsittely: 3 - 1 = 2
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Grey} 6} {\ peruuta {7}}} {\ overset {\ color {punainen} 15} {\ peruuta {5}}} 3 \\ - 4 {\ color {red} 9} 1 \\\ hline {\ color {Gray} 62} \ end {array}}}$	15 - 9 = 6
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {red} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ Cancel {5}}} 3 \\ - {\ color {red} 4} 91 \\\ hline {\ color {Gray} 262} \ end {array}}}$	6 - 4 = 2

Pystysuora vähennys ilman siirtoja

Osittaiset erot

Osittainen Erot menetelmä eroaa muista pystysuora vähennyslasku menetelmiä, että se ei käytön kuljettaa yli. Ne korvataan osittaisilla eroilla, joille annetaan plus- tai miinusmerkki sen mukaan, onko minuend tai subtrahend sarakkeessa suurempi. Osittaisten erojen summa johtaa kokonaiseroon.

esimerkki

	kuvaus
${\ displaystyle {\ begin {array} {rr} & {\ color {red} 7} 53 \\ - & {\ color {red} 4} 91 \\ hline {\ color {Gray} +} & {\ väri {harmaa} 300} \ loppu {matriisi}}}$	Pienempi luku vähennetään suuremmasta: 700 - 400 = 300 Koska minuend on suurempi kuin alaliitto, erolle annetaan plusmerkki.
${\ displaystyle {\ begin {array} {rr} & 7 {\ color {red} 5} 3 \\ - & 4 {\ color {red} 9} 1 \\\ hline {\ color {Gray} +} & {\ color {Gray} 300} \\ {\ color {Gray} -} ja {\ color {Gray} 40} \ end {array}}}$	Pienempi luku vähennetään suuremmasta: 90 - 50 = 40 Koska osa-ala on suurempi kuin minuend, erolle annetaan miinusmerkki.
${\ displaystyle {\ begin {array} {rr} & 75 {\ color {red} 3} \\ - & 49 {\ color {red} 1} \\\ hline {\ color {Grey} +} & {\ väri {harmaa} 300} \\ {\ väri {harmaa} -} ja {\ väri {harmaa} 40} \\ {\ väri {harmaa} +} ja {\ väri {harmaa} 2} \ loppu {matriisi}} }$	Pienempi luku vähennetään suuremmasta: 3 - 1 = 2 Koska minuend on suurempi kuin alaliitto, erolle annetaan plusmerkki.
${\ displaystyle {\ begin {array} {rr} & 753 \\ - & 491 \\\ hline {\ color {red} +} ja {\ color {red} 300} \\ {\ color {red} -} & {\ color {red} 40} \\ {\ color {red} +} ja {\ color {red} 2} \\\ hline & {\ color {Gray} 262} \ end {array}}}$	+ 300 - 40 + 2 = 262

Muut kuin vertikaaliset menettelyt

Ero on liioiteltu

Eroa ei tarvitse laskea numeroittain. Enimmäkseen hankala, mutta on myös mahdollista käydä läpi numeroalueen subtrahendin ja minuendin välillä.

esimerkki

1234-567 = voidaan laskea seuraavilla vaiheilla:

• 567 +  3  = 570
• 570 +  30  = 600
• 600 +  400  = 1000
• 1000 +  234  = 1234

Eron määrittämiseksi lisätään yksittäisten vaiheiden arvot: 3 + 30 + 400 + 234 = 667.

Alitunnistuksen hajoaminen

Toinen lähestymistapa, joka soveltuu yhtä hyvin kirjalliseen vähennykseen ja henkiseen aritmeettiseen toimintaan, on hajottaa alaosa, joka vähennetään minuendistä yksittäisissä vaiheissa.

esimerkki

"1234 - 567 =" voidaan laskea seuraavasti:

• 1234 -  500  = 734
• 734 -  60  = 674
• 674 -  7  = 667

Sama muutos

Sama muutos vähennys perustuu havaintoon, että vähennys on helppo toteuttaa, jos on yksi tai useampia nollia lopussa vähentäjä. Tällä menetelmällä osa-alaosaa kasvatetaan tai pienennetään lähimpään kymmeneen; koska minuendea kasvatetaan tai pienennetään samalla erolla, manipulaatiolla ei ole vaikutusta eroon. Jos tehtävä on sen jälkeen edelleen liian vaikea, operaatio voidaan toistaa.

esimerkki

"1234 - 567 =" voidaan laskea seuraavasti:

• 1234-567 = 1237-570 = 1267-600 = 667

nettilinkit

• Esimerkkejä irrotuksesta ja laajennustekniikasta (PDF-tiedosto; 39 kt)
• Omenat - Freeware-harjoitusohjelma kirjalliseen vähennykseen

Yksittäiset todisteet

1. ^ Rochester Institute of Technology : Toimintajärjestys
2. ^ Koulutuspaikka: Operaatiojärjestys
3. ↑ Khan Academy : Operaation järjestys ( video, klo 05:40 )
4. ^ Virginian opetusministeriö : Toimintajärjestyksen käyttäminen ja ominaisuuksien tutkiminen , kohta 9
5. ↑ Chemnitzin teknillinen yliopisto : Etusijasäännöt ja assosiatiivisuus
6. ^ Donald E.Knuth: Tietokoneohjelmoinnin taide, 2. osa: Seminumeriset algoritmit . 3. painos. Addison-Wesley, New York 1997, ISBN 978-0-201-89684-8 . 
7. ^ Monia aritmeettisia tapoja UCSMP: n jokapäiväisessä matematiikan vähennyslaskennassa: Vaihda ensin
8. ↑ Osittainen-erot vähennyslasku ( Memento of alkuperäisen 23 kesäkuu, 2014 Internet Archive ) Info: arkisto yhteys oli lisätään automaattisesti, ei ole vielä tarkastettu. Tarkista alkuperäinen ja arkistolinkki ohjeiden mukaisesti ja poista sitten tämä ilmoitus. ; Monia aritmeettisia tapoja UCSMP: n jokapäiväisessä matematiikan vähennyslaskussa: osittaiset erot @ 1@ 2Malline: Webachiv / IABot / ouronlineschools.org
9. ↑ UCSMP: n jokapäiväisen matematiikan vähennyslaskun monet aritmeettiset tavat : laskenta
10. ^ Monia aritmeettisia tapoja UCSMP: n päivittäisessä matematiikan vähennyslaskussa: Vasemmalta oikealle vähennyslasku
11. ^ Monia aritmeettisia tapoja UCSMP: n jokapäiväisessä matematiikan vähennyslaskussa: sama muutossääntö