Yksivaiheinen prosessi

Yksi-vaihe menetelmiä lähentää liuos (sininen) ja alkuarvon ongelman määrittämällä pistettä , jne., Yksi toisensa jälkeen annetusta lähtöpisteestä${\ displaystyle A_ {0}}$${\ displaystyle A_ {1}}$${\ displaystyle A_ {2}}$

On numeerinen matematiikka, yksi-vaihe menetelmiä ovat, on lisäksi monivaiheinen menetelmiä, suuri joukko laskentamenetelmiä ratkaisemiseksi alkuarvotehtävät . Tällä tehtävällä, jossa annetaan yhteinen differentiaaliyhtälö yhdessä lähtöehdon kanssa, on keskeinen rooli kaikissa luonnontieteissä ja tekniikan aloilla, ja siitä tulee yhä tärkeämpi esimerkiksi taloustieteessä ja yhteiskuntatieteessä. Alkuarvo-ongelmia käytetään dynaamisten prosessien analysointiin, simulointiin tai ennustamiseen.

Yksivaiheisen menetelmän nimi antaa perusajatuksen, että he laskevat annetusta lähtökohdasta lähentymispisteet askel askeleelta etsittyä ratkaisua pitkin. Tällöin he käyttävät seuraavaan vaiheeseen vain viimeisimmin määritettyä likiarvoa, toisin kuin monivaiheinen menetelmä, joka sisältää myös pisteitä, jotka olivat myöhemmin laskennassa. Yksivaiheiset menetelmät voidaan jakaa karkeasti kahteen ryhmään: eksplisiittisiin menetelmiin, jotka laskevat uuden likiarvon suoraan vanhasta, ja implisiittisiin menetelmiin, joissa yhtälö on ratkaistava. Jälkimmäiset soveltuvat myös niin kutsuttuihin jäykkiin alkuarvo-ongelmiin.

Yksinkertaisin ja vanhin yksivaiheinen menetelmä, nimenomainen Euler-menetelmä , julkaistiin vuonna 1768 Leonhard Euler . Sen jälkeen kun joukko monivaiheisia prosesseja oli esitetty vuonna 1883, noin vuonna 1900 Carl Runge , Karl Heun ja Wilhelm Kutta kehittivät merkittäviä parannuksia Eulerin prosessiin. Näistä syntyi suuri joukko Runge-Kutta-prosesseja , jotka muodostavat tärkeimmän yksivaiheisten prosessien luokan. 1900-luvun jatkokehitys on esimerkiksi ajatus ekstrapoloinnista , mutta ennen kaikkea vaiheiden koon säätämistä, eli sopivan pituuden valitsemista menetelmän yksittäisille vaiheille. Nämä käsitteet muodostavat perustan vaikeiden alkuarvo-ongelmien ratkaisemiselle, koska niitä esiintyy nykyaikaisissa sovelluksissa tehokkaasti ja tarvittavalla tarkkuudella tietokoneohjelmien avulla.

esittely

Tavalliset differentiaaliyhtälöt

Englantilaisen fyysikon ja matemaatikon Isaac Newtonin ja saksalaisen polymatin Gottfried Wilhelm Leibnizin tekemä differentiaalisen ja integraalilaskennan kehittäminen 1700-luvun viimeisellä kolmanneksella oli olennainen sysäys tieteen matematisoinnille varhaisen nykyaikana . Nämä menetelmät muodostivat analyysin matemaattisen haaran lähtökohdan, ja niillä on keskeinen merkitys kaikissa luonnontieteissä ja tekniikoissa . Vaikka Leibniziä johti geometrinen ongelma määrittää tangentit annetuille käyrille differentiaalilaskennalle, Newton lähti kysymyksestä, kuinka fyysisen määrän muutokset voidaan määrittää tietyllä ajankohdalla.

Esimerkiksi kun keho liikkuu, sen keskinopeus on yksinkertaisesti kuljettu matka jaettuna kuluneella ajalla. Kuitenkin, jotta matemaattisesti muotoilla nykyinen nopeus rungon sisään tiettynä ajankohtana , raja on ylitettävä: Yksi katsoo lyhyitä pituus , matkaan, ja siihen liittyvä keskimääräinen nopeus . Jos ajanjakson annetaan nollata ja jos keskinopeudet lähestyvät myös kiinteää arvoa , niin tätä arvoa kutsutaan (hetkelliseksi) nopeudeksi annetussa ajankohdassa . Kuvaa asemaa kehon tuolloin , sitten yksi kirjoituksia ja nimet johtaminen on . ${\ displaystyle v (t)}$${\ displaystyle t}$${\ displaystyle \ Delta t}$${\ displaystyle \ Delta x}$${\ displaystyle {\ tfrac {\ Delta x} {\ Delta t}}}$${\ displaystyle \ Delta t}$${\ displaystyle v (t)}$${\ displaystyle t}$${\ displaystyle x (t)}$${\ displaystyle t}$${\ displaystyle v (t) = x '(t)}$${\ displaystyle v}$${\ displaystyle x}$

Ratkaiseva askel differentiaaliyhtälömallien suuntaan on nyt päinvastainen kysymys: Liikkuvan kappaleen esimerkissä nopeus tunnetaan koko ajan ja sen sijainti on määritettävä siitä. On elävästi selvää, että myös ruumiin alkuasento on tiedettävä tietyllä hetkellä, jotta tämä ongelma voidaan ratkaista selvästi. Se on etsinnän funktio , jonka mukaan alkuperäinen ehto annetuilla arvoilla ja täyttyi. ${\ displaystyle t}$${\ displaystyle v (t)}$${\ displaystyle x (t)}$${\ displaystyle t_ {0}}$${\ displaystyle x (t)}$${\ displaystyle x '(t) = v (t)}$${\ displaystyle x (t_ {0}) = x_ {0}}$${\ displaystyle t_ {0}}$${\ displaystyle x_ {0}}$

Esimerkissä, jossa kehon sijainti määritetään sen nopeudesta, etsityn funktion johdanto on nimenomaisesti annettu. Yleensä on kuitenkin tärkeä yleisten tapausten tavanomaiset differentiaaliyhtälöt vaaditulle määrälle : Luontolakien tai malliehdotusten perusteella tiedetään toiminnallinen suhde, joka osoittaa kuinka määritettävän funktion derivaatti voidaan laskea ja (tuntemattomasta) arvosta . Lisäksi on jälleen oltava alkuehto, joka voidaan saada esimerkiksi mittaamalla vaadittu muuttuja kiinteänä ajankohtana. Yhteenvetona voidaan todeta, että meillä on seuraavan tyyppinen ongelma: Etsi funktio, joka sisältää yhtälöt ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle y '(t)}$${\ displaystyle t}$${\ displaystyle y (t)}$${\ displaystyle y}$

${\ displaystyle y '(t) = f (t, y (t)), \ quad y (t_ {0}) = y_ {0}}$

missä on tietty funktio. ${\ displaystyle f}$

Esitetty ratkaisu Lorenzin vetovoiman differentiaaliyhtälöstä on hyvin monimutkainen käyrä kolmiulotteisessa tilassa

Yksinkertainen esimerkki on koko, joka kasvaa räjähdysmäisesti . Tämä tarkoittaa sitä, että nykyinen muutos, eli johdannainen, on verrannollinen että itse. Joten sitä sovelletaan kasvunopeudella ja esimerkiksi alkuehdolla . Tällöin etsimäsi ratkaisu löytyy jo alkuerotuslaskelmasta ja määritetään eksponenttifunktion avulla : Se pätee . ${\ displaystyle y}$${\ displaystyle y '(t)}$ ${\ displaystyle y (t)}$${\ displaystyle y '(t) = \ lambda y (t)}$${\ displaystyle \ lambda}$${\ displaystyle y (0) = y_ {0}}$${\ displaystyle y}$${\ displaystyle y (t) = y_ {0} e ^ {\ lambda t}}$

Toiminnon vaatimukset on differentiaaliyhtälön voi olla vektori-arvo , joka on kunkin siellä voi olla vektori , jossa on komponentteja. Sitten puhutaan -dimensionaalisesta differentiaaliyhtälöjärjestelmästä. Tapauksessa liikkuvan elimen, sen asema ulotteinen euklidinen avaruus ja sen nopeus ovat sitten aikaan . Siksi differentiaaliyhtälö määrittää määritetyn liikeradan nopeuden suunnan ja suuruuden mukaan kullakin aika- ja avaruuspisteellä . Itse polku tulisi laskea tästä. ${\ displaystyle y}$${\ displaystyle t}$${\ displaystyle y (t) = (y_ {1} (t), \ dotsc, y_ {d} (t))}$${\ displaystyle d}$${\ displaystyle d}$${\ displaystyle y (t)}$${\ displaystyle d}$${\ displaystyle y '(t)}$${\ displaystyle t}$

Perusvaihe yksivaiheisesta prosessista

Kun esimerkkinä pidetään eksponentiaalisen kasvun yksinkertaista differentiaaliyhtälöä, ratkaisutoiminto voidaan määrittää suoraan. Yleensä tämä ei ole enää mahdollista monimutkaisemmilla ongelmilla. Tietyissä lisäedellytyksissä voidaan sitten näyttää funktiolle , että alkuperäisen arvon ongelmaan on olemassa yksilöllisesti määritetty ratkaisu; Tätä ei kuitenkaan voida enää erikseen laskea käyttämällä analyysimenetelmiä (kuten muuttujien erottaminen , eksponentiaalinen lähestymistapa tai vakioiden vaihtelu ). Tässä tapauksessa numeerisia menetelmiä voidaan käyttää etsimään ratkaisua. ${\ displaystyle f}$

Menetelmät tavallisten differentiaaliyhtälöiden alkuarvotehtävien numeeriseksi ratkaisemiseksi voidaan jakaa karkeasti kahteen suureen ryhmään: yksi- ja monivaiheinen menetelmä. Molemmilla ryhmillä on yhteistä, että ne laskevat vähitellen likiarvot haluttuille funktioarvoille pisteissä . Yksivaiheisen menetelmän määrittävä ominaisuus on, että vain ”nykyistä” likiarvoa käytetään seuraavan likiarvon määrittämiseen . Toisin kuin monivaiheisissa menetelmissä, sisällytetään myös aiemmin lasketut likiarvot; kolmivaiheisella menetelmällä käytettäisiin siis myös ja uuden likiarvon määrittämiseen . ${\ displaystyle y_ {0}, y_ {1}, y_ {2}, \ dotsc}$${\ displaystyle y (t_ {0}), y (t_ {1}), y (t_ {2}), \ dotsc}$${\ displaystyle t_ {0} <t_ {1} <t_ {2} <\ ldots}$${\ displaystyle y_ {j + 1}}$${\ displaystyle y_ {j}}$${\ displaystyle y_ {j}}$${\ displaystyle y_ {j-1}}$${\ displaystyle y_ {j-2}}$${\ displaystyle y_ {j + 1}}$

Kaksi vaihetta nimenomaisesta Euler-menetelmästä

Yksinkertaisin ja perustavin yksivaiheinen menetelmä on eksplisiittinen Euler-menetelmä , jonka sveitsiläinen matemaatikko ja fyysikko Leonhard Euler esitteli oppikirjassa Institutiones Calculi Integralis vuonna 1768 . Tämän menetelmän tarkoituksena on lähentää paloittain lineaarisen funktion etsimää ratkaisua, jossa suoran kaltevuus annetaan jokaisessa vaiheessa pisteestä toiseen . Tarkemmin: Ongelma antaa jo arvon etsittävälle toiminnolle, nimittäin . Mutta johdatus tässä vaiheessa on myös tiedossa, koska se pätee . Ratkaisufunktion graafin tangentti voidaan siten määrittää ja käyttää likiarvona. Tässä vaiheessa on askelkoko${\ displaystyle t_ {j}}$${\ displaystyle t_ {j + 1}}$${\ displaystyle f (t_ {j}, y_ {j})}$${\ displaystyle y (t_ {0}) = y_ {0}}$${\ displaystyle y '(t_ {0}) = f (t_ {0}, y_ {0})}$${\ displaystyle t_ {1}> t_ {0}}$${\ displaystyle h_ {0}: = t_ {1} -t_ {0}}$

${\ displaystyle y (t_ {1}) \ noin y_ {0} + h_ {0} f (t_ {0}, y_ {0}) =: y_ {1}}$.

Tätä menettelyä voidaan nyt jatkaa seuraavissa vaiheissa. Kaiken kaikkiaan tämä johtaa nimenomaisen Euler-menetelmän laskusääntöön

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} f (t_ {j}, y_ {j}), \ quad j = 0,1,2, \ dotsc}$

askelkokojen kanssa .${\ displaystyle h_ {j} = t_ {j + 1} -t_ {j}}$

Selkeä Euler-menetelmä on lähtökohta lukuisille yleistyksille, joissa rinne korvataan rinteillä, jotka arvioivat ratkaisun käyttäytymistä pisteiden välillä ja tarkemmin. Kaltevuutena käytetty implisiittinen Euler-menetelmä tarjoaa lisäidean yksivaiheisille menetelmille . Ensi silmäyksellä tämä valinta ei näytä sopivan, koska sitä ei tunneta. Yhtälö saadaan nyt menettelyvaiheeksi ${\ displaystyle f (t_ {j}, y_ {j})}$${\ displaystyle t_ {j}}$${\ displaystyle t_ {j + 1}}$${\ displaystyle f (t_ {j + 1}, y_ {j + 1})}$${\ displaystyle y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} f (t_ {j + 1}, y_ {j + 1})}$

josta (tarvittaessa numeerisella menetelmällä) voidaan laskea. Jos kaltevuudeksi valitaan esimerkiksi eksplisiittisen ja implisiittisen Euler-menetelmän kaltevuuksien aritmeettinen keskiarvo , saadaan implisiittinen puolisuunnikkaan muotoinen menetelmä . Tästä voidaan saada eksplisiittinen menetelmä, esimerkiksi jos approksimoidaan tuntemattomuus yhtälön oikealla puolella lähentämällä eksplisiittistä Euler-menetelmää, ns. Heun-menetelmää . Kaikilla näillä menettelyillä ja kaikilla muilla yleistyksillä on perusajatus yksivaiheisesta menettelystä: vaihe ${\ displaystyle y_ {j + 1}}$${\ displaystyle y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} \ Phi}$

kulmakertoimen , joka voi riippua , ja ja (tapauksessa implisiittinen menetelmät) päälle. ${\ displaystyle \ Phi}$${\ displaystyle t_ {j}}$${\ displaystyle y_ {j}}$${\ displaystyle h_ {j}}$${\ displaystyle y_ {j + 1}}$

määritelmä

Tämän artikkelin johdanto-osan huomioiden perusteella yksivaiheisen menettelyn käsite voidaan määritellä seuraavasti: Etsimme ratkaisua alkuarvo-ongelmaan ${\ displaystyle y}$

${\ displaystyle y '(t) = f (t, y (t))}$, .${\ displaystyle \ quad y (t_ {0}) = y_ {0}}$

Oletetaan, että ratkaisu

${\ displaystyle y \ kaksoispiste I \ to \ mathbb {R} ^ {d}}$

esiintyy tietyllä aikavälillä ja on yksilöllisesti määritetty. ovat ${\ displaystyle I = [t_ {0}, T]}$

${\ displaystyle t_ {0} <t_ {1} <t_ {2} <\ ldots <t_ {n} = T}$

Välipisteet välissä ja siihen liittyvät askelkoot, se tarkoittaa läpi ${\ displaystyle I}$${\ displaystyle h_ {j} = t_ {j + 1} -t_ {j}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} \ Phi (t_ {j}, y_ {j}, y_ {j + 1}, h_ {j})}$, ${\ displaystyle \ quad j = 0, \ dotsc, n-1}$

annetut menettelyt yksivaiheinen menettely ja toiminto . Jos se ei riipu, niin sitä kutsutaan yksiselitteiseksi yksivaiheiseksi menettelyksi . Muussa tapauksessa yhtälö yhtälölle on ratkaistava jokaisessa vaiheessa ja menettelyä kutsutaan implisiittiseksi .${\ displaystyle \ Phi}$${\ displaystyle \ Phi}$${\ displaystyle y_ {j + 1}}$${\ displaystyle j}$${\ displaystyle y_ {j + 1}}$

Johdonmukaisuus ja lähentyminen

Lähentymisjärjestys

Yleinen virhe eri askelkoissa kolmelle yksivaiheiselle menetelmälle. On kaksinkertainen logaritminen käyrä , suhde näyttää suunnilleen lineaarinen, rinteillä vastaavat lähentymisen tilauksia 1, 2 ja 4.${\ displaystyle h}$

Käytännöllisessä yksivaiheisessa menetelmässä tarkan ratkaisun arvojen laskettujen hyvien likiarvojen tulisi olla pisteessä . Koska määrät ovat yleensä -dimensionaalisia vektoreita, tämän approksimaation laatu mitataan vektorinormilla as , virheen pisteessä . On toivottavaa, että nämä virheet lähestyvät nopeasti nollaa kaikille, jos askelkokojen annetaan lähentyä nollaan. Jotta voidaan kattaa myös ei-vakioisten askelkokojen tapaus, määritellään tämä tarkemmin käytettyjen askelkokojen maksimiksi ja otetaan huomioon maksimivirheen käyttäytyminen kaikissa pisteissä verrattuna tehoihin . Sanotaan, että yksivaiheisella menettelyllä annetun lähtöarvo-ongelman ratkaisemiseksi on lähentymisjärjestys, jos estimaatti ${\ displaystyle y_ {j}}$${\ displaystyle y (t_ {j})}$${\ displaystyle y}$${\ displaystyle t_ {j}}$${\ displaystyle d}$${\ displaystyle \ | y_ {j} -y (t_ {j}) \ |}$${\ displaystyle t_ {j}}$${\ displaystyle j}$${\ displaystyle h}$${\ displaystyle t_ {j}}$${\ displaystyle h}$ ${\ displaystyle p \ geq 1}$

${\ displaystyle \ max _ {j = 0, \ dotsc, n} \ | y_ {j} -y (t_ {j}) \ | \ leq Ch ^ {p}}$

pätee kaikille riittävän pieniä , joiden vakio, joka on riippumaton .${\ displaystyle h}$${\ displaystyle h}$${\ displaystyle C> 0}$

Lähentymisjärjestys on tärkein parametri erilaisten yksivaiheisten menettelyjen vertailussa. Menetelmä, jolla on korkeampi konvergenssiluokka, tuottaa yleensä pienemmän kokonaisvirheen tietylle askelkokolle tai päinvastoin, vähemmän vaiheita tarvitaan tietyn tarkkuuden saavuttamiseksi. Menetelmän kanssa on odotettavissa, että jos askelkoko puolitetaan, virhe vain noin puolittuu. Lähentymisjärjestyksessä olevan menetelmän tapauksessa voidaan kuitenkin olettaa, että virhe pienenee suunnilleen kertoimella . ${\ displaystyle p}$${\ displaystyle p = 1}$${\ displaystyle p = 4}$${\ displaystyle {\ bigl (} {\ tfrac {1} {2}} {\ bigr)} ^ {4} = {\ tfrac {1} {16}}}$

Yleinen ja paikallinen virhe

Lähentymisjärjestyksen määrittelyssä huomioon otetut virheet koostuvat kahdesta yksittäisestä komponentista tavalla, joka vaikuttaa alun perin monimutkaiselta: Tietysti ne riippuvat toisaalta menettelyn yhdessä vaiheessa tekemästä virheestä, koska etsittävän toiminnon tuntematon kaltevuus korvataan likimääräisellä toimintotoiminnolla. Toisaalta on myös otettava huomioon, että vaiheen aloituspiste ei yleensä ole jo täsmällinen tarkan aloituskohdan kanssa ; tämän vaiheen jälkeinen virhe riippuu myös kaikista virheistä, jotka on jo tehty edellisissä vaiheissa. Yhden vaiheen menettelyn yhdenmukaisen määritelmän vuoksi, joka eroaa vain menettelytavan valinnassa, voidaan osoittaa, että (tietyissä teknisissä olosuhteissa ) lähentymismääräyksen voidaan päätellä suoraan virhemääräyksestä yhdessä vaiheessa, ns. johdonmukaisuusjärjestys . ${\ displaystyle \ | y_ {j} -y (t_ {j}) \ |}$${\ displaystyle (t_ {j}, y_ {j})}$${\ displaystyle (t_ {j}, y (t_ {j}))}}$${\ displaystyle \ Phi}$${\ displaystyle \ Phi}$

Johdonmukaisuuden käsite on yleinen ja keskeinen käsite nykyaikaisessa numeerisessa matematiikassa. Kun tutkitaan, kuinka hyvin numeeriset likiarvot sopivat tarkkaan ratkaisuun menettelyn lähentymisen aikana, kun on kyse johdonmukaisuudesta, yksinkertaisesti sanottuna, kysytään "päinvastainen" kysymys: Kuinka hyvin tarkka ratkaisu täyttää menettelyspesifikaation? Tässä yleisessä teoriassa on todettu, että menetelmä on yhteneväinen vain ja vain, jos se on johdonmukainen ja vakaa . Merkintöjen yksinkertaistamiseksi on seuraavassa harkittava, että nimenomainen yksivaiheinen menettely

${\ displaystyle y_ {j + 1} = y_ {j} + h \ Phi (t_ {j}, y_ {j}, h)}$

vakiona askelkoko . Todellinen ratkaisu määrittelee paikallisen leikkausvirheen (jota kutsutaan myös paikalliseksi menettelyvirheeksi ) muodossa${\ displaystyle h}$${\ displaystyle t \ mapsto y (t)}$${\ displaystyle \ eta}$

${\ displaystyle \ eta (t, h) = y (t) + h \ Phi (t, y (t), h) -y (t + h)}$.

Joten oletetaan, että tarkka ratkaisu on tiedossa, aloittaa prosessivaiheen siinä vaiheessa ja muodostaa eron pisteessä olevaan tarkkaan ratkaisuun . Tämä määrittelee: Yksivaiheisella menettelyllä on johdonmukaisuusjärjestys, jos arvio ${\ displaystyle (t, y (t))}}$${\ displaystyle t + h}$ ${\ displaystyle p \ geq 1}$

${\ displaystyle \ | \ eta (t, h) \ | \ leq Ch ^ {p + 1}}$

pätee kaikille riittävän pieniä , joiden vakio, joka on riippumaton . ${\ displaystyle h}$${\ displaystyle h}$${\ displaystyle C> 0}$

Huomattava ero johdonmukaisuusjärjestyksen ja lähentymisjärjestyksen määritelmien välillä on voiman sijasta . Tämä voidaan tulkita selkeästi siten, että askelkokoinen teho "menetetään" siirtyessä paikallisesta virheestä globaaliin. Seuraava lause, joka on keskeinen yksivaiheisen menettelyn teoriassa, pätee:${\ displaystyle h ^ {p + 1}}$${\ displaystyle h ^ {p}}$

Jos prosessitoiminto on jatkuva Lipschitz ja siihen liittyvällä yksivaiheisella prosessilla on johdonmukaisuusjärjestys , niin sillä on myös lähentymisjärjestys .${\ displaystyle \ Phi}$ ${\ displaystyle p}$${\ displaystyle p}$

Prosessitoiminnon Lipschitz-jatkuvuus vakauden lisävaatimuksena täyttyy yleensä aina, jos differentiaaliyhtälön funktio on itse Lipschitz-jatkuva. Tämä vaatimus on otettava useimmissa sovelluksissa joka tapauksessa, jotta taataan alkuperäisen arvon ongelman yksiselitteinen ratkaisukyky. Lauseen mukaan riittää määrittämään yksivaiheisen menettelyn johdonmukaisuusjärjestys. Periaatteessa tämä voidaan saavuttaa Taylorin ja on valtuudet . Käytännössä saadut korkeamman asteen kaavat muuttuvat hyvin monimutkaisiksi ja hämmentäviksi, joten tarvitaan lisäkäsitteitä ja merkintöjä.${\ displaystyle f}$${\ displaystyle \ eta (t, h)}$${\ displaystyle h}$

Jäykkyys ja A-vakaus

Menetelmän lähentymisjärjestys on asymptoottinen lausunto, joka kuvaa likiarvojen käyttäytymistä, kun askelkoko lähenee nollaa. Se ei kuitenkaan kerro mitään siitä, lasketaanko menetelmä tosiasiallisesti käyttökelpoinen likiarvo tietylle kiinteälle askelkokolle. Charles Francis Curtiss ja Joseph O. Hirschfelder kuvasivat ensimmäisen kerran vuonna 1952, että tämä voi todellakin olla suuri ongelma tietyntyyppisissä alkuarvo-ongelmissa.He ovat havainneet, että joidenkin kemiallisten reaktioiden kinetiikan differentiaaliyhtälöjärjestelmien ratkaisuja ei voida laskea käyttämällä numeerisia menetelmiä, ja he nimittivät heidät tällaisiksi alkuperäisiksi arvoiksi "jäykiksi". Tietyn ongelman jäykkyyden määrittämiseksi on olemassa useita matemaattisia kriteerejä. Jäykät alkuarvoongelmat ovat selvästi enimmäkseen differentiaaliyhtälöjärjestelmiä, joissa joistakin komponenteista tulee vakioita hyvin nopeasti, kun taas toiset komponentit muuttuvat vain hitaasti. Tällainen käyttäytyminen tapahtuu tyypillisesti kemiallisia reaktioita mallinnettaessa. Hyödyllisin jäykkyyden määritelmä käytännön sovelluksissa on: Alkuarvo-ongelma on jäykkä, jos joudutaan valitsemaan askelkoko "liian pieni" saadakseen käyttökelpoisen ratkaisun yksiselitteisellä yksivaiheisella menetelmällä. Tällaiset ongelmat voidaan ratkaista vain implisiittisillä menetelmillä.

Eksponentiaalisesti putoavan ratkaisun (sininen) laskemiseksi eksplisiittinen Euler-menetelmä (punainen) on täysin hyödytön, jos askelkoko on liian suuri; implisiittinen Euler-menetelmä (vihreä) määrittää ratkaisun laadullisesti oikein mille tahansa askelkokolle.

Tätä vaikutusta voidaan havainnollistaa tarkemmin tutkimalla, kuinka yksittäiset menetelmät selviävät eksponentiaalisesta hajoamisesta . Harkitse tätä varten ruotsalaisen matemaatikon Germund Dahlquistin testikaava

${\ displaystyle y '(t) = \ lambda y (t), \ quad y (0) = 1}$

jossa vähennetään eksponentiaalisesti liuos . Graafinen vastakohta osoittaa - esimerkkinä eksplisiittisestä ja implisiittisestä Euler-menetelmästä - näiden kahden menetelmäryhmän tyypillisen käyttäytymisen tässä näennäisen yksinkertaisessa alkuarvoongelmassa: Jos käytetään liian suurta askelkokoa eksplisiittisessä menetelmässä, voimakkaasti heilahteleva Tulokset, jotka ovat Build up -laskennassa ja siirtyvät yhä kauemmas tarkasta ratkaisusta. Toisaalta implisiittiset menetelmät laskevat tyypillisesti ratkaisun laadullisesti oikein kaikille askelkoille, nimittäin eksponentiaalisesti laskevana likimääräisten arvojen jaksona.${\ displaystyle \ lambda <0}$${\ displaystyle y (t) = e ^ {\ lambda t}}$

Edellä olevaa testiyhtälöä pidetään myös jonkin verran yleisemmin arvojen kompleksisten arvojen suhteen . Tässä tapauksessa ratkaisujen värähtelyt, joiden amplitudi pysyy rajoitettuna, jos mahdollista , ts. Todellinen komponentti on pienempi tai yhtä suuri kuin 0. Tämä mahdollistaa yhden vaiheen menetelmien toivotun ominaisuuden muotoilun, joita on käytettävä jäykkiin alkuarvo-ongelmiin: niin sanottu A-stabiilisuus. Menetelmä on nimeltään A-stabiili, jos se on sovellettu testi yhtälö tahansa koko ja lasketaan kaikkien kanssa sekvenssin arvioita , jotka (kuten todellinen liuos) pysyy rajoitettu. Epäsuora Euler-menetelmä ja implisiittinen puolisuunnikkaan muotoinen menetelmä ovat yksinkertaisimpia esimerkkejä A-stabiileista yksivaiheisista menetelmistä. Toisaalta voidaan osoittaa, että nimenomainen menettely ei voi koskaan olla A-vakaa.${\ displaystyle \ lambda}$${\ displaystyle \ operaattorin nimi {Re} (\ lambda) \ leq 0}$${\ displaystyle \ lambda}$${\ displaystyle h> 0}$${\ displaystyle \ lambda}$${\ displaystyle \ operaattorin nimi {Re} (\ lambda) \ leq 0}$${\ displaystyle y_ {0}, y_ {1}, y_ {2}, \ dotsc}$

Erityiset menettelyt ja menettelytavat

Joitakin yhden vaiheen menettelyjä verrattuna

Yksinkertaiset menettelyt järjestyksessä 1 ja 2

Kuten Ranskan matemaatikko Augustin Louis Cauchy osoittautui noin 1820, Euler menetelmä on suuruusluokkaa lähentymisen 1. Jos rinteillä nimenomaisen Eulerin ja implisiittinen Eulerin , sellaisena kuin ne ovat kahden päätepisteen on välivaihe, voi olla keskimääräinen toivo saada parempi likiarvo koko intervallin ajan. Itse asiassa voidaan osoittaa, että näin saatu implisiittinen puolisuunnikkaan muotoinen menetelmä${\ displaystyle f (t_ {j}, y_ {j})}$${\ displaystyle f (t_ {j + 1}, y_ {j + 1})}$

${\ displaystyle y_ {j + 1} = y_ {j} + {\ frac {h} {2}} {\ iso (} f (t_ {j}, y_ {j}) + f (t_ {j + 1 }, y_ {j + 1}) {\ iso)}}$

lähentymismääräyksellä on 2. Tällä menetelmällä on erittäin hyvät stabiiliusominaisuudet, mutta se on implisiittinen, joten yhtälö arvolle on ratkaistava jokaisessa vaiheessa . Jos tämä määrä arvioidaan yhtälön oikealla puolella käyttäen eksplisiittistä Euler-menetelmää, Heunin eksplisiittinen menetelmä johtaa${\ displaystyle y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + {\ frac {h} {2}} {\ iso (} f (t_ {j}, y_ {j}) + f {\ iso (} t_ {j + 1}, y_ {j} + hf (t_ {j}, y_ {j}) {\ iso)} {\ iso)}}$,

jolla on myös lähentymisjärjestys 2. Toinen yksinkertainen selkeä menetelmä järjestyksessä 2, parannettu Euler-menetelmä , voidaan saada ottamalla huomioon seuraavat seikat: "Keskimääräinen" kaltevuus prosessivaiheessa olisi liuoksen kaltevuus vaiheen keskellä eli kohdassa . Koska ratkaisua ei kuitenkaan tunneta, se arvioidaan nimenomaisella Euler-askeleella, jossa on puolet askelkokosta. Menettelysääntö johtaa ${\ displaystyle y}$${\ displaystyle t_ {j} + {\ tfrac {h} {2}}}$

${\ displaystyle y_ {j + 1} = y_ {j} + hf {\ iso (} t_ {j} + {\ tfrac {h} {2}}, y_ {j} + {\ tfrac {h} {2 }} f (t_ {j}, y_ {j}) {\ iso)}}$.

Nämä saksalaisen matemaatikko Carl Runge julkaisivat nämä tilauksen 2 yksivaiheiset menetelmät vuonna 1895 parannuksina Euler-menetelmään .

Runge-Kutta-menetelmä

Klassisessa neljännen asteen Runge-Kutta -menetelmässä keskimäärin neljä apurinteitä (punainen) kussakin vaiheessa

Edellä mainitut ideat yksinkertaisista yksivaiheisista menetelmistä johtavat Runge-Kutta-menetelmien tärkeään luokkaan, jos niitä edelleen yleistetään. Esimerkiksi Heunin menetelmä voidaan esittää selkeämmin seuraavasti: Ensin lasketaan apukaltevuus, nimittäin eksplisiittisen Euler-menetelmän kaltevuus. Tämä määrittää toisen apukaltevuuden tässä . Tosiasiallisesti käytetty prosessigradientti saadaan sitten lisägradienttien painotettuna keskiarvona Heun-menetelmällä . Tämä menettely voidaan yleistää useammalle kuin kahdelle apukaltevuudelle. A- vaiheinen Runge-Kutta-menetelmä laskee ensin apugradientit arvioimalla ne sopivissa pisteissä ja sitten painotettuna keskiarvona. Selkeän Runge-Kutta-menetelmän tapauksessa apukaltevuudet lasketaan suoraan peräkkäin; implisiittisen menetelmän tapauksessa ne johtuvat ratkaisuina yhtälöjärjestelmään. Tyypillinen esimerkki on selkeä, klassinen Runge-Kutta menetelmä järjestyksessä 4, joka on joskus kutsutaan yksinkertaisesti Runge-Kutta menetelmä: Ensin, neljä ylimääräiset kaltevuudet ovat käytettyjen ${\ displaystyle k_ {1} = f (t_ {j}, y_ {j})}$${\ displaystyle k_ {2} = f (t_ {j} + h, y_ {j} + hk_ {1})}$${\ displaystyle \ Phi}$${\ displaystyle {\ tfrac {1} {2}} k_ {1} + {\ tfrac {1} {2}} k_ {2}}$${\ displaystyle s}$${\ displaystyle k_ {1}, \ dotsc, k_ {s}}$${\ displaystyle f}$${\ displaystyle \ Phi}$${\ displaystyle k_ {1}, k_ {2}, k_ {3}, \ dotsc}$

${\ displaystyle {\ begin {tasattu} k_ {1} & = f (t_ {j}, y_ {j}) \\ k_ {2} & = f (t_ {j} + {\ tfrac {h} {2 }}, y_ {j} + {\ tfrac {h} {2}} k_ {1}) \\ k_ {3} & = f (t_ {j} + {\ tfrac {h} {2}}, y_ {j} + {\ tfrac {h} {2}} k_ {2}) \\ k_ {4} & = f (t_ {j} + h, y_ {j} + hk_ {3}) \ loppu {tasattu }}}$

ja sitten painotettu keskiarvo prosessin kaltevuutena

${\ displaystyle {\ tfrac {1} {6}} k_ {1} + {\ tfrac {1} {3}} k_ {2} + {\ tfrac {1} {3}} k_ {3} + {\ tfrac {1} {6}} k_ {4}}$

käytetty. Saksalaisen matemaatikko Wilhelm Kutta julkaisi tämän tunnetun menetelmän vuonna 1901, kun Karl Heun oli löytänyt 3-vaiheisen yksivaiheisen menetelmän vuosi 3 aiemmin .

Vielä korkeamman asteen eksplisiittisten prosessien rakentaminen mahdollisimman pienellä määrällä vaiheita on matemaattisesti erittäin vaativa ongelma. Kuten John C. Butcher pystyi osoittamaan vuonna 1965, tilauksessa 5 on esimerkiksi vain vähintään kuuden vaiheen menettelyt; 8. asteen nimenomainen Runge-Kutta-menetelmä vaatii vähintään 11 ​​vaihetta. Vuonna 1978 itävaltalainen matemaatikko Ernst Hairer löysi järjestyksen 10 mukaisen menettelyn 17 vaiheella. Tällaisen menettelyn kertoimien on täytettävä 1205 määrittävää yhtälöä. Implisiittisten Runge-Kutta -menetelmien tapauksessa tilanne on yksinkertaisempi ja selkeämpi: jokaiselle vaiheiden lukumäärälle on järjestysmenetelmä ; tämä on samalla suurin mahdollinen järjestys.${\ displaystyle s}$${\ displaystyle p = 2s}$

Ekstrapolointimenetelmä

Ajatus ekstrapoloinnista ei rajoitu alkuarvo-ongelmien ratkaisemiseen yksivaiheisilla menetelmillä, vaan sitä voidaan soveltaa analogisesti kaikkiin numeerisiin menetelmiin, jotka diskretisoivat ratkaistavan ongelman askelkoolla . Tunnettu esimerkki ekstrapolointimenetelmästä on Rombergin integraatio integraalien numeeriseen laskemiseen. Olkoon siis yleensä arvo, joka on määritettävä numeerisesti, tässä artikkelissa esimerkiksi alkuarvo-ongelman ratkaisufunktion arvo tietyssä pisteessä. Numeerinen menetelmä, esimerkiksi yksivaiheinen menetelmä, laskee tälle likimääräisen arvon , joka riippuu askelkoon valinnasta . Tässä oletetaan, että menetelmä on yhtenevä, eli että vastaan jos suppenee suppenee nollaan. Tämä lähentyminen on kuitenkin vain puhtaasti teoreettinen lausunto, koska menetelmän tosiasiallisessa soveltamisessa likimääräiset arvot voidaan laskea rajalliselle määrälle eri askelkokoja , mutta tietysti et voi antaa vaihekoon "lähentyä nollaan". Laskettu likiarvoja eri kokoja voidaan kuitenkin ymmärrettävä tietoa (tuntematon) toiminto : Kun ekstrapolointi menetelmä , interpolointia polynomi käytetään kuin approksimaatio, eli polynomi , jossa on ${\ displaystyle h}$${\ displaystyle v}$${\ displaystyle {\ tilde {v}} (h)}$${\ displaystyle h> 0}$${\ displaystyle {\ tilde {v}} (h)}$${\ displaystyle v}$${\ displaystyle h}$${\ displaystyle {\ tilde {v}} (h_ {1}), {\ tilde {v}} (h_ {2}), \ dotsc, {\ tilde {v}} (h_ {m})}$${\ displaystyle h_ {1}> h_ {2}> \ ldots> h_ {m}}$${\ displaystyle {\ tilde {v}}}$${\ displaystyle {\ tilde {v}}}$${\ displaystyle P}$

${\ displaystyle P (h_ {k}) = {\ tilde {v}} (h_ {k})}$

varten . Arvo polynomin pisteessä käytetään sitten laskettavissa approksimaatio ei-laskettavissa raja varten kohti nollaa. Roland Bulirsch ja Josef Stoer julkaisivat varhaisen onnistuneen ekstrapolointialgoritmin alkuperäisiin arvo-ongelmiin vuonna 1966.${\ displaystyle k = 1,2, \ dotsc, m}$${\ displaystyle P (0)}$${\ displaystyle h = 0}$${\ displaystyle {\ tilde {v}} (h)}$${\ displaystyle h}$

Ekstrapolointi järjestysmenettelyssä${\ displaystyle h = 0}$${\ displaystyle p = 2}$

Konkreettinen esimerkki yksivaiheisen tilausmenetelmän tapauksessa voi tehdä yleisen ekstrapolointimenettelyn ymmärrettäväksi. Tällaisella menetelmällä laskettu likiarvo pienille askelkoille voidaan helposti muuntaa muodon polynomiksi ${\ displaystyle p}$${\ displaystyle h}$

${\ displaystyle P (h) = a + bh ^ {p}}$

aluksi tuntemattomilla parametreillä ja likimääräinen. Jos nyt käytetään menettelyä laskemaan kaksi likiarvoa ja yhdelle askelkokolle ja puolelle askelkokoa , saadaan interpolointiolosuhteista ja kahdesta lineaarisesta yhtälöstä tuntemattomille ja . Arvo ekstrapoloidaan ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle h_ {1}}$${\ displaystyle h_ {2} = {\ tfrac {1} {2}} h_ {1}}$${\ displaystyle y_ {h_ {1}}}$${\ displaystyle y_ {h_ {2}}}$${\ displaystyle P (h_ {1}) = y_ {h_ {1}}}$${\ displaystyle P (h_ {2}) = y_ {h_ {2}}}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle h = 0}$

${\ displaystyle P (0) = a = y_ {h_ {2}} + {\ frac {y_ {h_ {2}} - y_ {h_ {1}}} {2 ^ {p} -1}}}$

sitten edustaa yleensä paljon parempaa likiarvoa kuin kaksi alun perin laskettua arvoa. Voidaan osoittaa, että tällä tavalla saadun yksivaiheisen prosessin järjestys on vähintään , ts. Vähintään 1 suurempi kuin alkuperäisessä prosessissa.${\ displaystyle p + 1}$

Menettely portaiden koon säädöllä

Yksi yksivaiheisen menetelmän etu on, että mitä tahansa askelkokoa voidaan käyttää kussakin vaiheessa muista vaiheista riippumatta . Käytännössä tämä luonnollisesti herättää kysymyksen siitä, miten valita . Todellisissa sovelluksissa on aina virhetoleranssi, jolla alkuarvo-ongelman ratkaisu lasketaan; Esimerkiksi olisi turhaa määrittää numeerinen likiarvio, joka on merkittävästi "tarkempi" kuin tiedot, joissa on mittausvirheet annetun ongelman lähtöarvoille ja parametreille. Tavoitteena on siis valita askelkoot niin, että toisaalta noudatetaan määritettyjä virhetoleransseja, mutta toisaalta käytetään mahdollisimman vähän vaiheita pitämään laskennallinen vaivannäkö pienenä. Yleensä tämä voidaan saavuttaa vain, jos askelkoot sovitetaan ratkaisun kulkuun: pienet portaat, joissa ratkaisu muuttuu merkittävästi, suuret portaat, joissa se on melkein vakio.${\ displaystyle j}$${\ displaystyle h_ {j}}$ ${\ displaystyle h_ {j}}$

Tapauksessa hyvin ilmastoituja alkuarvotehtävät, voidaan osoittaa, että maailmanlaajuinen menettelyyn virhe on suunnilleen yhtä suuri kuin paikallisen pyöristysvirheet yksittäisissä vaiheissa. Siksi tulisi valita mahdollisimman suuri askelkoko , joka on alle valitun toleranssikynnyksen. Ongelmana on, että sitä ei voida laskea suoraan, koska se riippuu alkuperäisen arvon ongelman tuntemattomasta tarkasta ratkaisusta pisteessä . Portaiden koon säätämisen perusajatuksena on siis lähentää menetelmää, joka on tarkempi kuin perusmenetelmä, johon se perustuu.${\ displaystyle \ eta _ {j}: = \ | \ eta (t_ {j}, h_ {j}) \ |}$${\ displaystyle h_ {j}}$${\ displaystyle \ eta _ {j}}$${\ displaystyle \ eta _ {j}}$${\ displaystyle y (t_ {j})}$${\ displaystyle t_ {j}}$${\ displaystyle y (t_ {j})}$

Kaksi askelkokokontrollin perusideoita ovat puolittaa askelkoko ja upotetut menettelyt . Puolitettaessa askelkoko lasketaan kahden vaiheen tulos, jossa on puolet askelkoosta, vertailuarvona todellisen prosessivaiheen lisäksi. Tarkempi likiarvo arvolle määritetään sitten molemmista arvoista ekstrapoloimalla ja siten arvioidaan paikallinen virhe . Jos tämä on liian suuri, tämä vaihe hylätään ja toistetaan pienemmällä askelmalla. Jos se on merkittävästi pienempi kuin määritetty toleranssi, askelkokoa voidaan lisätä seuraavassa vaiheessa. Lisälaskentaponnistus tälle askelkoon puolittamismenetelmälle on suhteellisen suuri; siksi nykyaikaisissa toteutuksissa käytetään enimmäkseen ns. upotettuja menetelmiä askelkokojen säätämiseen. Perusidea on laskea kaksi likiarvoa kullekin vaiheelle käyttämällä kahta yksivaiheista menetelmää, joilla on erilaiset lähentymisjärjestykset, ja siten arvioida paikallinen virhe. Laskentaponnistelujen optimoimiseksi kahdella menettelyllä tulisi olla mahdollisimman monta laskentavaihetta yhteistä: Niiden tulisi olla "upotettuja toisiinsa". Esimerkiksi sulautetuissa Runge-Kutta -menetelmissä käytetään samoja apurinteitä ja ne eroavat toisistaan ​​vain niiden keskiarvon suhteen. Tunnettuja sulautettuja menetelmiä ovat Runge-Kutta-Fehlberg -menetelmät ( Erwin Fehlberg , 1969) ja Dormand-Prince-menetelmät (JR Dormand ja PJ Prince, 1980).${\ displaystyle y (t_ {j})}$${\ displaystyle \ eta _ {j}}$${\ displaystyle y (t_ {j})}$

Käytännön esimerkki: Alkuarvo-ongelmien ratkaiseminen numeerisella ohjelmistolla

Tämän artikkelin yleiskatsauksessa esitetyille matemaattisille käsitteille on kehitetty lukuisia ohjelmistototeutuksia, joiden avulla käyttäjä voi ratkaista käytännön ongelmat numeerisesti yksinkertaisella tavalla. Konkreettisena esimerkkinä Lotka-Volterra-yhtälöiden ratkaisu on laskettava laajasti käytetyllä Matlab- ohjelmistolla . Lotka-Volterra yhtälöt ovat yksinkertainen malli biologian, joka kuvaa vuorovaikutukset saalistajan ja saaliin populaatiot . Tätä varten annetaan differentiaaliyhtälöjärjestelmä

${\ displaystyle {\ begin {aligned} y_ {1} '(t) & = ay_ {1} (t) -by_ {1} (t) y_ {2} (t) \\ y_ {2}' (t ) & = cy_ {1} (t) y_ {2} (t) -dy_ {2} (t) \ loppu {tasattu}}}$

- parametrit ja lähtöehto , - . Täällä ja vastaavat saalista tai saalistajien populaation ajallista kehitystä. Liuos tulisi laskea aikavälin mukaan . ${\ displaystyle a = 1, b = 2, c = 1, d = 1}$${\ displaystyle y_ {1} (0) = 3}$${\ displaystyle y_ {2} (0) = 1}$${\ displaystyle y_ {1}}$${\ displaystyle y_ {2}}$${\ displaystyle [0,20]}$

Matlabia käytettäessä lasketaan ensin differentiaaliyhtälön oikealla puolella oleva funktio annetuille parametriarvoille : ${\ displaystyle f}$${\ displaystyle y '= f (t, y)}$

a = 1; b = 2; c = 1; d = 1;
f = @(t,y) [a*y(1) - b*y(1)*y(2); c*y(1)*y(2) - d*y(2)];

Lisäksi vaaditaan aikaväli ja alkuarvot:

t_int = [0, 20];
y0 = [3; 1];

Sitten ratkaisu voidaan laskea:

[t, y] = ode45(f, t_int, y0);

Matlab-funktio ode45toteuttaa yksivaiheisen menetelmän, joka käyttää kahta upotettua eksplisiittistä Runge-Kutta-menetelmää, joiden konvergenssiluokitukset 4 ja 5 ovat vaiheiden koon säätämiseen.

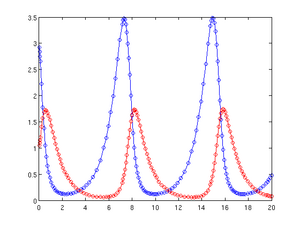
Ratkaisu voidaan nyt piirtää sinisenä käyränä ja punaisena käyränä ; lasketut pisteet on merkitty pienillä ympyröillä: ${\ displaystyle y_ {1}}$${\ displaystyle y_ {2}}$

figure(1)
plot(t, y(:,1), 'b-o', t, y(:,2), 'r-o')

Tulos näkyy alla olevassa kuvassa vasemmalla. Oikea kuva näyttää prosessin käyttämät askelkoot, jotka on luotu

figure(2)
plot(t(1:end-1), diff(t))

Lotka-Volterra-yhtälöiden ratkaisut

Käytetyt lisäykset

Tämä esimerkki voidaan suorittaa myös ilmaisella numeerisella ohjelmistolla GNU Octave ilman muutoksia . Siellä toteutetun menetelmän kanssa on kuitenkin jonkin verran erilainen askelkokosekvenssi.

kirjallisuus

• John C. Butcher : Numeeriset menetelmät tavallisille differentiaaliyhtälöille . John Wiley & Sons, Chichester 2008, ISBN 978-0-470-72335-7 . 
• Wolfgang Dahmen , Arnold Reusken: Numerot insinööreille ja luonnontieteilijöille . 2. painos. Springer, Berliini / Heidelberg 2008, ISBN 978-3-540-76492-2 , luku. 11: Tavalliset differentiaaliyhtälöt . 
• Peter Deuflhard , Folkmar Bornemann : Numeerinen matematiikka 2 - tavalliset differentiaaliyhtälöt . 3. painos. Walter de Gruyter, Berliini 2008, ISBN 978-3-11-020356-1 . 
• David F.Griffiths, Desmond J.Higham: Numeeriset menetelmät tavallisille differentiaaliyhtälöille - alkuarvo-ongelmat . Springer, Lontoo 2010, ISBN 978-0-85729-147-9 . 
• Robert Plato: Numeerisen matematiikan kompakti . 4. painos. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , luku. 7: Yksivaiheinen menettely alkuarvoongelmille . 
• Hans-Jürgen Reinhardt: Tavallisten differentiaaliyhtälöiden numerot . 2. painos. Walter de Gruyter, Berliini / Boston 2012, ISBN 978-3-11-028045-6 . 
• Hans Rudolf Schwarz, Norbert Köckler: Numeerinen matematiikka . 8. painos. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1551-4 , luku. 8: Alkuarvo-ongelmat . 
• Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Tavallisten differentiaaliyhtälöiden numerot . 2. painos. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 . 

nettilinkit

• Lars Grüne: Numeeriset menetelmät tavallisille differentiaaliyhtälöille (numeerinen matematiikka II). (PDF) 2008, käyty 20. elokuuta 2018 ( Bayreuthin yliopiston luentomuistiinpanot ). 
• Peter Spellucci: Tavallisten differentiaaliyhtälöiden numerot . (PDF) 2007, luettu 20. elokuuta 2018 (luentomuistiinpanot TU Darmstadtilta ). 
• Hans U. Fuchs: Numeeriset menetelmät differentiaaliyhtälöille. (PDF) 2007, käyty 20. elokuuta 2018 (englanti, luentotiedot Zürichin ammattikorkeakoulusta ). 
• Matemaattinen opetusohjelma: ensimmäisen kertaluvun yleinen differentiaaliyhtälälaskuri. Julkaisussa: Matematiikan opetusohjelma. Haettu 20. elokuuta 2018 . 

Yksittäiset todisteet

1. ^ Thomas Sonar : 3000 vuotta analyysia . Springer, Berliini / Heidelberg 2011, ISBN 978-3-642-17203-8 , s. 378-388 ja 401-426 . 
2. ↑ Jean-Luc Chabert ym.: Algoritmien historia . Springer, Berliini / Heidelberg 1999, ISBN 978-3-540-63369-3 , s. 374-378 . 
3. ↑ Wolfgang Dahmen, Arnold Reusken: numeerinen analyysi insinööreille ja tutkijoille . 2. painos. Springer, Berliini / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 386 f . 
4. ↑ Wolfgang Dahmen, Arnold Reusken: numeerinen analyysi insinööreille ja tutkijoille . 2. painos. Springer, Berliini / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 386-392 . 
5. ↑ Hans Rudolf Schwarz, Norbert Köckler: Numeerinen matematiikka . 8. painos. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1551-4 , s. 350 f . 
6. ^ Robert Plato: Numeerisen matematiikan kompakti . 4. painos. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , s. 157 . 
7. ^ Robert Plato: Numeerisen matematiikan kompakti . 4. painos. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , s. 156 . 
8. ^ Robert Plato: Numeerisen matematiikan kompakti . 4. painos. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , s. 157 . 
9. ↑ Hans-Jürgen Reinhardt: Tavallisten differentiaaliyhtälöiden numerot . 2. painos. Walter de Gruyter, Berliini / Boston 2012, ISBN 978-3-11-028045-6 , s. 42 f . 
10. ^ John C. Butcher: Numeeriset menetelmät tavallisille differentiaaliyhtälöille . John Wiley & Sons, Chichester 2008, ISBN 978-0-470-72335-7 , s. 95-100 . 
11. ^ JC Butcher: Numeeriset menetelmät tavallisille differentiaaliyhtälöille 1900-luvulla . Julkaisussa: Journal of Computational and Applied Mathematics . nauha 125 , ei. 1-2 , 15. joulukuuta 2000, s. 21 f . ( verkossa ). 
12. ↑ Peter Deuflhard, Folkmar Bornemann: Numeerinen matematiikka 2 - Tavalliset differentiaaliyhtälöt . 3. painos. Walter de Gruyter, Berliini 2008, ISBN 978-3-11-020356-1 , s. 228 f . 
13. ↑ Peter Deuflhard, Folkmar Bornemann: Numeerinen matematiikka 2 - Tavalliset differentiaaliyhtälöt . 3. painos. Walter de Gruyter, Berliini 2008, ISBN 978-3-11-020356-1 , s. 229-231 . 
14. ↑ Wolfgang Dahmen, Arnold Reusken: numeerinen analyysi insinööreille ja tutkijoille . 2. painos. Springer, Berliini / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 443 f . 
15. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Tavallisten differentiaaliyhtälöiden numerot . 2. painos. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 258 f . 
16. ↑ Jean-Luc Chabert ym.: Algoritmien historia . Springer, Berliini / Heidelberg 1999, ISBN 978-3-540-63369-3 , s. 378 f . 
17. ↑ Jean-Luc Chabert ym.: Algoritmien historia . Springer, Berliini / Heidelberg 1999, ISBN 978-3-540-63369-3 , s. 381-388 . 
18. ↑ Wolfgang Dahmen, Arnold Reusken: numeerinen analyysi insinööreille ja tutkijoille . 2. painos. Springer, Berliini / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 406 f . 
19. ^ JC Butcher: Numeeriset menetelmät tavallisille differentiaaliyhtälöille 1900-luvulla . Julkaisussa: Journal of Computational and Applied Mathematics . nauha 125 , ei. 1-2 , 15. joulukuuta 2000, s. 4-6 ( verkossa ). 
20. ↑ Peter Deuflhard, Folkmar Bornemann: Numeerinen matematiikka 2 - Tavalliset differentiaaliyhtälöt . 3. painos. Walter de Gruyter, Berliini 2008, ISBN 978-3-11-020356-1 , s. 160-162 . 
21. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Tavallisten differentiaaliyhtälöiden numerot . 2. painos. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 219-221 . 
22. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Tavallisten differentiaaliyhtälöiden numerot . 2. painos. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 79 ff . 
23. ^ JC Butcher: Numeeriset menetelmät tavallisille differentiaaliyhtälöille 1900-luvulla . Julkaisussa: Journal of Computational and Applied Mathematics . nauha 125 , ei. 1-2 , 15. joulukuuta 2000, s. 26 ( verkossa ). 
24. ^ Robert Plato: Numeerisen matematiikan kompakti . 4. painos. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , s. 171-173 . 
25. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Tavallisten differentiaaliyhtälöiden numerot . 2. painos. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 57-59 . 
26. ↑ Peter Deuflhard, Folkmar Bornemann: Numeerinen matematiikka 2 - Tavalliset differentiaaliyhtälöt . 3. painos. Walter de Gruyter, Berliini 2008, ISBN 978-3-11-020356-1 , s. 199-204 . 
27. ^ Robert Plato: Numeerisen matematiikan kompakti . 4. painos. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , luku. 7: Yksivaiheinen menetelmä alkuarvoongelmille , s. 173-177 . 
28. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Tavallisten differentiaaliyhtälöiden numerot . 2. painos. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 64-70 . 
29. ↑ ode45: ratkaista nonstiff differentiaaliyhtälöiden - väliaineessa, jotta menetelmä. MathWorks, käyty 23. marraskuuta 2017 .