Euklidinen tila

Vuonna matematiikka The euklidinen avaruus on ensinnäkin ”avaruus meidän intuitio”, koska se on kuvattu Euklideen elementit mukaan aksioomat ja postulaatit (vrt Euklidinen geometria ). 1800-luvulle asti oletettiin, että tämä kuvasi meitä ympäröivää fyysistä tilaa . Lisäys "Euklidinen" tuli välttämättömäksi sen jälkeen, kun matematiikassa oli kehitetty yleisempiä avaruuskäsitteitä (esim. Hyperbolinen tila , Riemannin jakotukit ), ja erityisen ja yleisen suhteellisuusteorian yhteydessä kävi ilmi, että muita avaruuskäsitteitä tarvitaan kuvaamaan tilaa fysiikassa ( Minkowski-tila , Lorentz-jakotukki ).

Ajan myötä Euclidin geometriaa tarkennettiin ja yleistettiin useilla tavoilla:

• Hilbertin aksiomaattisesti ( katso Hilbertin euklidisen geometrian aksioomajärjestelmä ),
• kuten vektori tila (a vektori tila on määritelty , jonka skalaaritulo ),${\ displaystyle \ mathbb {R}}$
• kuten euklidinen kohta tila (an affiini tila mallintaa yli vektori tila),
• kuten koordinaatistossa kanssa standardin skalaaritulo .${\ displaystyle \ mathbb {R} ^ {3}}$

Kun euklidinen tila mainitaan, mitä tahansa näistä määritelmistä voidaan tarkoittaa tai korkeamman ulottuvuuden yleistyksiä. Kaksiulotteista euklidista avaruutta kutsutaan myös euklidiseksi tasoksi . Tässä kaksiulotteisessa tapauksessa termi on yleisempi synteettisessä geometriassa : euklidiset tasot voidaan määritellä siellä affinitasoina yleisemmälle kappaleille, euklidisille kappaleille . Nämä rungot ovat (mielipiteestäsi riippuen) osarunkoja tai isomorfisia rungoille${\ displaystyle \ mathbb {R}.}$

Euklidinen tila eroaa affiinisesta avaruudesta siinä, että pituudet ja kulmat voidaan mitata. Siksi piirretään kuvat, jotka sisältävät pituuksia ja kulmia. Näitä kutsutaan perinteisesti kongruenssikartoiksi , muut termit ovat liikkeet ja isometriikat .

Kun ei-Euclidean tilat , kuten hyperbolisen ja elliptinen työskentelytiloissa, selviö yhtäläisyyksiä ei sovelleta.

Euklidiset vektoritilat

Euklidisesta intuitiosta euklidiseen vektoritilaan

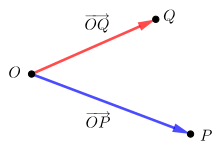
In analyyttinen geometria , euklidinen tila on annettu vektori tilaa . Yksi mahdollisuus tehdä tämä on ottaa suorituksen mukana toimitettujen rinnakkaisten siirtymien (käännösten) määrä lisäykseksi. Jokainen siirtymä voidaan kuvata nuolella, joka yhdistää pisteen sen kuvapisteeseen. Kaksi nuolta, jotka ovat yhdensuuntaisia ​​samaan suuntaan ja joilla on sama pituus, kuvaavat samaa siirtymää. Kahta tällaista nuolta kutsutaan ekvivalenteiksi ja ekvivalenssiluokkia kutsutaan vektoreiksi .

Jos valitaan piste Euclidean tilan kuin referenssipiste ( alkuperä ), voidaan määrittää jokaisen pisteen asemaansa vektori , vektori, joka edustaa nuoli alkuperää kohtaan . Tällä tavoin ihmissuhde saadaan aikaan euklidisen avaruuden ja siihen liittyvän euklidisen vektoritilan välillä ja voidaan siten tunnistaa alkuperäinen euklidinen tila euklidisen vektoritilan kanssa. Tämä tunnistaminen ei kuitenkaan ole kanonista, vaan riippuu alkuperän valinnasta. ${\ displaystyle O}$${\ displaystyle P}$ ${\ displaystyle {\ vec {p}} = {\ ylisuuri {OP}}}$${\ displaystyle O}$${\ displaystyle P}$

Voidaan nyt myös siirtää pituus- ja kulmamittaukset euklidisesta avaruudesta vektoreihin liittyvien nuolien ja kulmien pituudella niiden välillä. Tällä tavalla saadaan vektoritila skalaarisen tuloksen kanssa . Skalaarituotteelle on tunnusomaista se, että vektorin tulo itsessään on sen pituuden neliö . Kaava saadaan laskutoimitusskaaleista, binomi kaavoista ja kosini-laista (sovellettu kolmioon, jonka sivut vastaavat vektoreita , ja ) ${\ displaystyle {\ vec {a}} \ cdot {\ vec {a}}}$${\ displaystyle {\ vec {a}}}$${\ displaystyle | {\ vec {a}} | ^ {2}}$${\ displaystyle | {\ vec {a}} |}$${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}}}$${\ displaystyle {\ vec {b}} - {\ vec {a}}}$

${\ displaystyle {\ vec {a}} \ cdot {\ vec {b}} = | {\ vec {a}} | \, | {\ vec {b}} | \, \ cos \ pallomaiset kulmat ({\ vec {a}}, {\ vec {b}})}$.

Tässä tarkoittaa vektorien ja . ${\ displaystyle \ pallomainen kulma ({\ vec {a}}, {\ vec {b}})}$${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}}}$

Yleinen termi

Tästä eteenpäin kutakin kutakin todellista vektoriavaruutta, jolla on skalaarinen tulo (mikä tahansa äärellinen ulottuvuus ) , kutsutaan euklidiseksi vektoritilaksi . Edellä olevaa kaavaa käytetään sitten määrittämään vektorin pituus ( normi ) ja vektorien välinen kulma. Kaksi vektoria ovat kohtisuorassa, jos niiden skalaarinen tulo on nolla. Jokainen kolmiulotteinen euklidinen vektoriavaruus on isometrisesti isomorfinen nuoliluokkien vektoriavaruuteen nähden. Jokainen dimensioinen euklidinen vektoriavaruus on isometrisesti isomorfinen koordinaattivektoriavaruuteen nähden (katso alla). Siksi saman ulottuvuuden euklidiset vektoritilat eivät ole erotettavissa. Tämä oikeuttaa yhden nimetä kutakin kuten vektori tilaan ulottuvuus . Jotkut kirjoittajat käyttävät myös termiä euklidinen avaruus äärettömän ulotteisiin todellisiin vektoritiloihin skalaarisen tuloksen kanssa, jotkut myös monimutkaisiin vektoritiloihin skalaarisen tuloksen kanssa, vrt. Piste tuotetila . ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle n}$${\ displaystyle n}$

Pituudet, kulmat, ortogonaalisuus ja ortonormaalipohjat

Heti kun on annettu todellinen vektoritila skalaarituotteella, voidaan siirtää euklidisen intuitioavaruuden metriset käsitteet tähän. Pituus (jäljempänä normi , määrä ) vektorin on silloin juuri skalaaritulo vektorin itsensä kanssa: ${\ displaystyle {\ vec {a}}}$

${\ displaystyle | {\ vec {a}} | = {\ sqrt {{\ vec {a}} \ cdot {\ vec {a}}}}}$.

Kaksi vektoria on kohtisuorassa (tai kohtisuorassa ) toisiinsa, jos niiden skalaarinen tulo on nolla: ${\ displaystyle {\ vec {a}}, {\ vec {b}}}$

${\ displaystyle {\ vec {a}} \ perp {\ vec {b}} \ Leftightarrow {\ vec {a}} \ cdot {\ vec {b}} = 0}$.

Kahden vektorin välinen (ei-suuntautunut) kulma määritetään käyttämällä yllä olevaa kaavaa

${\ displaystyle {\ vec {a}} \ cdot {\ vec {b}} = | {\ vec {a}} | \, | {\ vec {b}} | \, \ cos \ pallomaiset kulmat ({\ vec {a}}, {\ vec {b}})}$,

niin

${\ displaystyle \ sphericalangle ({\ vec {a}}, {\ vec {b}}) = \ arccos {\ frac {{\ vec {a}} \ cdot {\ vec {b}}} {| {\ vec {a}} | \, | {\ vec {b}} |}}}$.

Vektori kutsutaan yksikkö vektori , jos se on pituus 1. Perusteella koostuu yksikön vektoreita, jotka ovat pareittain ortogonaalisia kutsutaan ortonormaali kanta . Ortonormaalit emäkset ovat jokaisessa euklidisessa vektoriavaruudessa. Jos on ortonormaalipohja, vektori voidaan esittää tällä perusteella: ${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {e}} _ {1}, \ dotsc, {\ vec {e}} _ {n}}$${\ displaystyle {\ vec {a}}}$

${\ displaystyle {\ vec {a}} = a_ {1} {\ vec {e}} _ {1} + \ piste + + a_ {n} {\ vec {e}} _ {n}}$.

Kertoimet saadaan laskemalla

${\ displaystyle a_ {i} = {\ vec {a}} \ cdot {\ vec {e}} _ {i}}$.

Isometriikka

Jos ja ovat kaksi- ulotteinen vektori tilat, lineaarinen kartoitus kutsutaan a kappale (lineaarinen) isometria jos se sisältää skalaaritulo, eli jos ${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle n}$${\ displaystyle f \ kaksoispiste V \ - W}$

${\ displaystyle f ({\ vec {a}}) \ cdot f ({\ vec {b}}) = {\ vec {a}} \ cdot {\ vec {b}}}$

koskee kaikkia . Tällaista kartoitusta kutsutaan myös ortogonaaliseksi kartoitukseksi . Isometrialle annetaan erityisesti pituudet ${\ displaystyle {\ vec {a}}, {\ vec {b}} \ in V}$${\ displaystyle f}$

${\ displaystyle | f ({\ vec {a}}) | = | {\ vec {a}} |}$

ja kulmat, erityisesti ortogonaalisuus

${\ displaystyle f ({\ vec {a}}) \ perp f ({\ vec {b}}) \ Longleftrightarrow {\ vec {a}} \ perp {\ vec {b}}.}$

Päinvastoin mikä tahansa lineaarinen kartoitus, joka vastaanottaa pituudet, on isometria.

Isometria kartoittaa jokaisen ortonormaalipohjan takaisin ortonormaalipohjaan. Toisaalta, jos ortonormaalin perusteella ja ortonormaalin perusteella , niin on olemassa isometrinen kuva, joka on karttoja. ${\ displaystyle {\ vec {e}} _ {1}, \ dotsc, {\ vec {e}} _ {n}}$${\ displaystyle V}$${\ displaystyle {\ vec {e}} _ {1} {} ', \ dotsc, {\ vec {e}} _ {n} {}'}$${\ displaystyle W}$${\ displaystyle {\ vec {e}} _ {i}}$${\ displaystyle {\ vec {e}} _ {i} {} '}$

Tämä tarkoittaa, että kaksi saman ulottuvuuden euklidista vektoriavaruutta ovat isometrisiä, toisin sanoen niitä ei voida erottaa euklidisina vektoreina.

Euklidinen pisteavaruus

motivaatio

Euklidiset vektoritilat toimivat usein euklidisen avaruuden malleina. Vektoritilan elementtejä kutsutaan sitten pisteiksi tai vektoreiksi kontekstista riippuen. Pisteitä ja niiden sijaintivektoreita ei tehdä eroa. Tämä voi olla laskennallisesti edullista. Käsitteellisesti se ei kuitenkaan ole tyydyttävä:

• Geometriselta kannalta pisteet ja vektorit tulisi erottaa käsitteellisesti.
  • Vektorit voidaan lisätä ja kertoa numeroilla, mutta pisteet eivät.
  • Pisteet on kytketty vektoreilla tai yhdistetty toisiinsa.
• Vektoritilassa on erinomainen elementti, nollavektori . Euklidisessa geometriassa kaikki pisteet ovat kuitenkin samat.

kuvaus

Euklidisen pisteavaruuden käsite tarjoaa parannuksen . Tämä on affiniteettitila euklidisen vektoriavaruuden päällä. Tässä tehdään ero pisteiden ja vektorien välillä.

• Pisteiden kokonaisuus muodostaa euklidisen pisteavaruuden. Tämä on tavallisesti , , tai , vastaavasti. (Yläindeksi ei ole eksponentti, vaan indeksi, joka luonnehtii ulottuvuutta. Joten se ei ole suorakulmainen tulo.)${\ displaystyle E}$${\ displaystyle E_ {n}}$${\ displaystyle E ^ {n}}$${\ displaystyle \ mathbb {E} ^ {n}}$${\ displaystyle n}$${\ displaystyle E ^ {n}}$
• Kaikkien vektorien kokonaisuus muodostaa euklidisen vektoritilan .${\ displaystyle V}$

• Jokaista kahta pistettä ja on täsmälleen yksi yhteys vektori, joka on merkitty. Pisteen yhteysvektori itsensä kanssa on nollavektori:${\ displaystyle P}$${\ displaystyle Q \ E: ssä}$${\ displaystyle {\ overrightarrow {PQ}}}$
  ${\ displaystyle {\ overrightarrow {PP}} = {\ vec {0}}}$
• Piste voidaan muuntaa pisteeksi yksiselitteisellä tavalla vektorin avulla . Tätä kutsutaan usein nimellä. (Tämä on puhtaasti muodollinen merkintätapa. Plus-merkki ei tarkoita mitään vektoriavaruuden lisäystä eikä myöskään lisäystä pistetilaan.) Nollavektori johtaa jokaisen vektorin itseensä:${\ displaystyle P}$${\ displaystyle {\ vec {v}}}$${\ displaystyle Q}$${\ displaystyle P + {\ vec {v}}}$
  ${\ displaystyle P + {\ vec {0}} = P}$
• Jos vektori johtaa piste tulee piste ja vektorin johtaa piste tulee piste , sitten piste johtaa osaksi kohta . Tämä voidaan ilmaista seuraavasti: ${\ displaystyle {\ vec {v}}}$${\ displaystyle P}$${\ displaystyle Q}$${\ displaystyle {\ vec {w}}}$${\ displaystyle Q}$${\ displaystyle R}$${\ displaystyle {\ vec {v}} + {\ vec {w}}}$${\ displaystyle P}$${\ displaystyle R}$

  ${\ displaystyle (P + {\ vec {v}}) + {\ vec {w}} = P + ({\ vec {v}} + {\ vec {w}})}$

  ${\ displaystyle {\ overrightarrow {PQ}} + {\ overrightarrow {QR}} = {\ overrightarrow {PR}}}$

Algebran kielellä nämä ominaisuudet tarkoittavat: Vektoriavaruuden additiivinen ryhmä toimii joukossa vapaasti ja siirtyvästi . ${\ displaystyle V}$ ${\ displaystyle E}$

Pituudet, etäisyydet ja kulmat

Linjojen pituudet, pisteiden väliset etäisyydet, kulmat ja ortogonaalisuus voidaan nyt määritellä vektorien skalaarisen tuloksen avulla:

Pituus linjan ja etäisyys pisteiden ja on määritelty pituus vektorin : ${\ displaystyle {\ overline {PQ}}}$ ${\ displaystyle [PQ]}$ ${\ displaystyle d (P, Q)}$${\ displaystyle P}$${\ displaystyle Q}$${\ displaystyle {\ overrightarrow {PQ}}}$

${\ displaystyle d (P, Q) = {\ overline {PQ}} = | {\ ylisuuri {PQ}} |}$

Kulman koko määritellään kulmana vektorien ja : ${\ displaystyle \ pallomainen nelikulma QPR}$${\ displaystyle {\ overrightarrow {PQ}}}$${\ displaystyle {\ overrightarrow {PR}}}$

${\ displaystyle \ sphericalangle QPR = \ sphericalangle ({\ overrightarrow {PQ}}, {\ overrightarrow {PR}})}$

Kaksi viivaa ja ovat ortogonaalisia vain ja vain, jos niihin liittyvät vektorit ja ovat ortogonaalisia. ${\ displaystyle [PQ]}$${\ displaystyle [RS]}$${\ displaystyle {\ overrightarrow {PQ}}}$${\ displaystyle {\ ylisuuri {RS}}}$

Kuvat

Euklidisen pisteavaruuden pituudeltaan säilyviä esityksiä kutsutaan isometriaksi , kongruenssikartoiksi (tasogeometriassa) tai liikkeiksi . Saat myös kulmat automaattisesti. Jos tapahtuu liikettä, tapahtuu ortogonaalinen kartoitus (lineaarinen isometria) siten, että kaikille pisteille ja : ${\ displaystyle f \ kaksoispiste E \ E}$${\ displaystyle {\ vec {f}} \ kaksoispiste V \ - V}$${\ displaystyle P}$${\ displaystyle Q}$

${\ displaystyle f (Q) = f (P) + {\ vec {f}} ({\ overrightarrow {PQ}})}$

Todellinen koordinaatitila

määritelmä

Ulotteinen todellinen koordinaatistossa on kertainen karteesinen tuote joukon todellinen määrä, eli joukko -Tuples jossa todelliset luvut ovat. Kontekstista riippuen elementtejä kutsutaan pisteiksi tai vektoreiksi, joten pisteiden ja vektorien välillä ei tehdä eroa. ${\ displaystyle n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle n}$${\ displaystyle \ mathbb {R}}$${\ displaystyle n}$${\ displaystyle x = (x_ {1}, \ dotsc, x_ {n})}$${\ displaystyle x_ {i}}$${\ displaystyle \ mathbb {R} ^ {n}}$

Vektoreina ne lisätään komponentti kerrallaan ja kerrotaan reaaliluvuilla:

${\ displaystyle x + y = (x_ {1}, \ dotsc, x_ {n}) + (y_ {1}, \ dotsc, y_ {n}) = (x_ {1} + y_ {1}, \ dotsc , x_ {n} + y_ {n})}$

${\ displaystyle r \, x = r \, (x_ {1}, \ dotsc, x_ {n}) = (rx_ {1}, \ dotsc, rx_ {n})}$

Tässä tapauksessa usein (ts. Sarakevektoreina - matriiseina ) elementit kirjoittivat: ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle (n \ kertaa 1)}$

${\ displaystyle x = {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}}; \ y = {\ begin {pmatrix} y_ {1} \\\ vdots \ \ y_ {n} \ end {pmatrix}}; \ x + y = {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}} + {\ begin {pmatrix} y_ {1} \\\ vdots \\ y_ {n} \ end {pmatrix}} = {\ begin {pmatrix} x_ {1} + y_ {1} \\\ vdots \\ x_ {n} + y_ {n } \ end {pmatrix}}; \ r \, x = r {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}} = {\ begin {pmatrix} rx_ { 1} \\\ vdots \\ rx_ {n} \ end {pmatrix}}}$

Skalaarituote ( tavallinen skalaarituote ) on määritelty

${\ displaystyle x \ cdot y = (x_ {1}, \ dotsc, x_ {n}) \ cdot (y_ {1}, \ dotsc, y_ {n}) = {\ aloita {pmatrix} x_ {1} \ \\ vdots \\ x_ {n} \ end {pmatrix}} \ cdot {\ begin {pmatrix} y_ {1} \\\ vdots \\ y_ {n} \ end {pmatrix}} = x_ {1} y_ { 1} + \ pistepiste + x_ {n} y_ {n}}$.

Tämän skalaarisen tuloksen avulla se on euklidinen vektoriavaruus. ${\ displaystyle \ mathbb {R} ^ {n}}$

Euklidisesta vektoritilasta / pistetilasta koordinaatiosta

Jos joku valitsee ortonormaalin perustan Eukleidesen vektoriavaruudessa tai suorakulmaisen koordinaatiston Euclidean pisteavaruudessa (ts. Koordinaattialkuperä ja vektoriavaruuden ortonormaali perusta), täten jokaiselle vektorille tai pisteelle osoitetaan koordinaattikuppi . Tällä tavalla saadaan isometria tietyn euklidisen avaruuden ja koordinaattitilan välillä ja ne voidaan tunnistaa keskenään tämän isometrian avulla. Tämän vuoksi on perusteltua, että koska nimitetyn euklidinen avaruus. Isometria riippuu kuitenkin ortonormaalin perustan valinnasta ja - pistetilan ollessa kyseessä - alkuperän valinnasta. ${\ displaystyle n}$${\ displaystyle \ mathbb {R} ^ {n}}$

Pituus, kulma, ortogonaalisuus, vakio pohja ja väli

Kuten kaikissa euklidisissa vektoriavaruuksissa, vektorin pituus tai normi annetaan skalaarisen tuloksen neliöjuurella itsensä kanssa:

${\ displaystyle | x | = {\ sqrt {x \ cdot x}} = {\ sqrt {x_ {1} ^ {2} + \ dotsb + x_ {n} ^ {2}}}}$

Tätä normia kutsutaan myös euklidiseksi normiksi tai 2-normiksi ja se kirjoittaa myös tai -merkin sijaan . ${\ displaystyle | x |}$${\ displaystyle \ lVert x \ rVert}$${\ displaystyle \ lVert x \ rVert _ {2}}$

Välinen kulma kaksi vektoria ja lasketaan sitten läpi ${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle \ cos \ pallokulma (x, y) = {\ frac {x \ cdot y} {| x | \, | y |}} = {\ frac {x_ {1} y_ {1} + \ piste + x_ {n} y_ {n}} {{\ sqrt {x_ {1} ^ {2} + \ dotsb + x_ {n} ^ {2}}} {\ sqrt {y_ {1} ^ {2} + \ piste + y_ {n} ^ {2}}}}}}$

Kaksi vektoria ja ovat ortogonaalisia vain ja vain ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle x \ perp y}$

${\ displaystyle x \ cdot y = x_ {1} y_ {1} + \ piste + + x_ {n} y_ {n} = 0}$

sovelletaan. Vektorit vakioperusteesta

${\ displaystyle e_ {1} = (1.0, \ dotsc, 0.0) \, \ quad e_ {2} = (0.1, \ dotsc, 0.0) \, \ quad \ dotsc \, \ quad e_ {n} = (0,0, \ dotsc, 0,1)}$

ovat yksikkövektoreita ja ortogonaalisia pareittain, ts. ne muodostavat ortonormaalin perustan .

Jos otetaan huomioon pisteiden elementit, määritetään pisteiden välinen etäisyys ja yhteysvektorin pituus : ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle yx}$

${\ displaystyle d (x, y) = | yx | = {\ sqrt {(yx) \ cdot (yx)}} = {\ sqrt {(y_ {1} -x_ {1}) ^ {2} + \ piste + + (y_ {n} -x_ {n}) ^ {2}}}}$

Isometriikka

Vektoriavaruudessa isometrics (lineaarinen isometries) ovat ortogonaalisia karttoja edustaa mukaan ortogonaalisia matriiseja . Onko lineaarinen isometrinen piirustus ja on ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle f \ kaksoispiste \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {n}}$

${\ displaystyle f (e_ {j}) = {\ aloita {pmatrix} a_ {1j} \\\ vdots \\ a_ {nj} \ end {pmatrix}} \}$

kuva nnen standardin perusteella vektori ( ) voidaan esittää käyttäen apuna matriisitulo kuin ${\ displaystyle j}$${\ displaystyle j = 1, \ dotsc, n}$${\ displaystyle f (x)}$

${\ displaystyle f (x) = Ax = {\ begin {pmatrix} a_ {11} & \ dotso & a_ {1n} \\\ vdots && \ vdots \\ a_ {n1} & \ dotso & a_ {nn} \ end { pmatrix}} {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}}}$.

Jokainen isometria ( liikkuminen ) ja pisteen tila voidaan ilmaista muodossa ${\ displaystyle f \ kaksoispiste \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {n}}$

${\ displaystyle f (x) = Ax + b = {\ begin {pmatrix} a_ {11} & \ dotso & a_ {1n} \\\ vdots && \ vdots \\ a_ {n1} & \ pisteet ja a_ {nn} \ end {pmatrix}} {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}} + {\ begin {pmatrix} b_ {1} \\\ vdots \\ b_ { n} \ end {pmatrix}}}$

linkkinä ortogonaalisen kartoituksen ja rinnakkaissiirron (käännös) välillä . ${\ displaystyle x \ mapsto Axe}$${\ displaystyle x \ mapsto x + b}$

suuntautuminen

Jokainen finite-ulotteinen todellinen vektori tilaa voidaan varustettu kanssa orientaation mukaan valitsemalla tilattu perusteella . Vaikka minkään euklidisen vektorin ja pisteavaruuden kohdalle ei ole merkitty suuntausta, koordinaatitilalla on kanoninen suuntaus, jonka standardipohja antaa: Vektorien järjestetty perusta on positiivisesti suuntautunut. ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle e_ {1}, \ dotsc, e_ {n}}$

Järjestetty perusta

${\ displaystyle a_ {1} = {\ aloita {pmatrix} a_ {11} \\ a_ {21} \\\ vdots \\ a_ {n1} \ end {pmatrix}}, \ a_ {2} = {\ alku {pmatrix} a_ {12} \\ a_ {22} \\\ vdots \\ a_ {n2} \ end {pmatrix}}, \ \ dotsc, \ a_ {n} = {\ begin {pmatrix} a_ {1n} \\ a_ {2n} \\\ vdots \\ a_ {nn} \ end {pmatrix}}}$

on positiivisesti suuntautunut vain ja vain, jos siitä muodostunut determinantti on positiivinen:

${\ displaystyle \ det (a_ {1}, a_ {2}, \ dotsc, a_ {n}) = {\ aloita {vmatrix} a_ {11} & a_ {12} & \ dotso & a_ {1n} \\ a_ { 21} & a_ {22} & \ dotso & a_ {2n} \\\ vdots & \ vdots & \ ddots & \ vdots \\ a_ {n1} & a_ {n2} & \ dotso & a_ {nn} \ end {vmatrix}}> 0}$

Jos fyysinen tila (jonka oletetaan olevan euklidinen) tunnistetaan koordinaatitilaan tuomalla suorakulmainen koordinaatisto , koordinaatti-akselit valitaan yleensä siten, että ne muodostavat oikean järjestelmän . Orientaatio fyysinen tila antama jonka oikean käden sääntö vastaa tällöin kanoninen orientaation koordinaatistossa . ${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle \ mathbb {R} ^ {3}}$

Euklidinen tila muilla matematiikan alueilla

Euklidiset tilat topologiassa

Funktio, joka määrittää kullekin vektorille skalaaritulon määrittelemän pituuden, on normi . Puhutaan skalaarituotteen tai skalaarisen tuotteen normin indusoimasta normista ; jotkut kirjoittajat kutsuvat normia myös euklidiseksi normiksi . Normaalin skalaarituotteen indusoimaa normia kutsutaan euklidiseksi normiksi tai 2-normiksi ja se on p- normien erityistapaus . Indusoidun normin seurauksena jokaisesta euklidisesta vektoriavaruudesta tulee normalisoitu tila ja siten klassinen esimerkki topologisesta vektoriavaruudesta . Erityisesti se on Prehilbert-tila, ja koska se on täydellinen myös rajallisessa ulottuvuudessa , Banach-tila ja siten myös Hilbert-tila . ${\ displaystyle \ mathbb {R} ^ {n}}$

Euklidisen etäisyyden funktio muuttuu joka euklidisen avaruuden metrinen avaruus ja siten erityisesti osaksi topologinen avaruus . ${\ displaystyle d (P, Q) = | {\ ylisuuri nuoli {PQ}} |}$

Koska kaikki normit ovat rajallisten ulottuvuuksien vektoritiloissa samanarvoisia , euklidisen avaruuden topologia ei todellakaan ole riippuvainen euklidisesta rakenteesta. Saman äärellisen ulottuvuuden normalisoidut vektoritilat ovat siis kaikki homeomorfisia toisilleen ja siten homeomorfisia . Sen jälkeen, kun joukko invariance ulottuvuus on Luitzen EJ Brouwer Euclidean tilat eri ulottuvuuden ei homeomorphic peräkkäisiä kuvattavan. ${\ displaystyle n}$${\ displaystyle \ mathbb {R} ^ {n}}$

Topologisena avaruutena euklidinen tila on vierekkäinen ja supistettavissa .

Euklidiset tilat differentiaalisessa topologiassa

Jakotukit on mallinnettu euklidisten tilojen yli: Jakotukki on paikallisesti homeomorfinen . Johtuen differentiable rakenteen derivoituva venttiilejä paikallisesti diffeomorfiset sen . Erityisesti euklidinen tila on itsessään erilaistuva moninaiset. Kaikille ulottuvuuksille, paitsi ulottuvuudelle 4, liian homeomorfinen erotettavissa oleva jakotukki on myös liian diffeomorfinen. Neljässä ulottuvuudessa olevia poikkeuksia kutsutaan eksoottisiksi 4-huoneisiksi . ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {n}}$

Euklidiset tilat differentiaaligeometriassa

Skalaarituote (joka ei ole pisteestä riippuvainen) muuttaa euklidisen avaruuden Riemannin monikerrokseksi . Käänteisesti Riemannin geometria, joka Riemannin pakosarja, joka on isometrinen vektorin tilan kanssa standardi skalaaritulo kutsutaan euklidisen tilaa. Näille Riemannian-jakotukille kaarevuustensori katoaa , eli tila on tasainen. Päinvastoin, jokainen tasainen Riemannin-jakotukki on paikallisesti isometrinen Euklidisen avaruuteen nähden. Se voi kuitenkin olla myös avoin osajoukko tai jakotukki, jonka yleinen päällekkäisyys on osajoukko . Kaksiulotteisia esimerkkejä jälkimmäiseen tapaukseen ovat tasainen torus tai suora pyöreä sylinteri . Toisaalta jokainen täydellinen ja yksinkertaisesti yhdistetty tasainen Riemannin-jakotukki on euklidinen tila. ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {n}}$

kirjallisuus

• Marcel Berger: Geometria I. Ranskalaisilta M. Cole ja S. Levy. Yliopiston teksti. Springer-Verlag, Berliini 1987, ISBN 3-540-11658-3 .
• Marcel Berger: Geometria II, ranskalaisilta M. Cole ja S. Levy. Yliopiston teksti. Springer-Verlag, Berliini 1987, ISBN 3-540-17015-4 .