Riemannin zeta -toiminto

Zeta -funktion funktiokaavio todellisille argumentteille alueella -20 < s <10

Kompleksikaavio funktion arvojen värillä : Riemannin zeta -funktio kompleksitasossa: Nolla eli kompleksitason alkuperä sijaitsee tarkalleen kaavion keskellä. Kuvassa näkyvät ns. Ei-triviaalit zeta-funktion nollat ​​sijaitsevat pystysuoralla viivalla 0,5, jota ei näytetä. Ne ovat tunnistettavissa mustina pisteinä tällä kuvitteellisella viivalla ja ne on järjestetty peilisymmetrisesti todelliseen akseliin, ts. Alkuperäisen kautta kulkevaan vaakasuoraan viivaan nähden. Kaaviossa on yksi puhdas valkoinen piste. Tämä kuuluu kuvion 1 zeta -funktion ainoaan napaan, eli siihen pisteeseen, joka on yksi yksikkö alkuperästä oikealla ja jossa zeta -funktiota ei ole määritelty. Niin sanotut triviaalit nollat ​​sijaitsevat todellisen akselin vasemmalla puolella, nimittäin −2, −4, −6, −8 ...

Riemannin Zeta funktio , myös Riemannin ζ funktio tai Riemannin Zeta funktio (kun Bernhard Riemannin ), on kompleksiarvoinen , erityinen matemaattinen funktio , joka on tärkeä rooli vuonna analyyttinen lukuteoria , eli haara on matematiikka . Leonhard Euler tutki sitä ensimmäisen kerran 1700 -luvulla osana Baselin ongelmaa . Se on yleensä kutsutaan symbolilla (kirjaimella zeta ), jossa Kompleksiluvun on sen verkkotunnuksen . ${\ displaystyle \ zeta (s)}$${\ displaystyle s}$

Arvoille , joiden todellinen osa on suurempi kuin 1, Riemannin zeta -funktio määritetään käyttämällä Dirichlet -sarjaa . Avulla analyyttinen jatkaminen , se voidaan laajennetaan on holomorphic funktio. Se täyttää tärkeän toiminnallisen yhtälön , jonka avulla sitä voidaan jopa kuvata. ${\ displaystyle s \ in \ mathbb {C}}$${\ displaystyle \ mathbb {C} \ setminus \ {1 \}}$

On erittäin tärkeää numero teoria, että Zeta funktio analyyttisesti seuraa lain yksiselitteinen hajoaminen luonnollisia lukuja osaksi alkutekijät (tämä tarkoittaa hajoamista numeron "jakamaton" elementtejä, noin 132 = 2 · 2 · 3 · 11 ), eli suljetun kaavan avulla . Tämän perusteella Riemann pystyi vuonna 1859 osoittamaan hyvin läheisen ja epäselvän suhteen alkuluvujen ja zeta-funktion nollien sijainnin välillä . Niin se johtuu siitä kaikille kompleksiluvut kanssa , että nnen alkuluku on arvo ”melko tarkalleen” - tarkemmin tästä seuraa${\ displaystyle \ zeta (s) \ neq 0}$ ${\ displaystyle s}$${\ displaystyle \ operaattorinimi {Re} (t) \ geq 1}$${\ displaystyle n}$${\ displaystyle p_ {n}}$${\ displaystyle n \ log (n)}$

${\ displaystyle \ lim _ {n \ to \ infty} {\ frac {p_ {n}} {n \ log (n)}} = 1.}$

Tarkoittaa tässä luonnollinen logaritmi on . Tarkemmat tiedot nolla-alueista tekevät kuvan alkuluvun jakauman ympärillä selkeämmäksi. Riemannin hypoteesissa , jota ei ole todistettu tähän päivään asti (syyskuusta 2020 lähtien), todetaan, että kaikki Riemannin zeta-funktion ei-triviaalit nollat ​​ovat todellinen osa , eli ne sijaitsevat yhteisellä suoralla viivalla. Onko tämä olettamus oikea vai ei, on yksi matematiikan tärkeimmistä ratkaisemattomista ongelmista . Koska alkuluvut ovat tärkeitä nykyaikaisille salausjärjestelmille (kuten RSA -salaus ), Riemannin hypoteesi saa huomiota myös puhtaan lukuteorian ulkopuolella. ${\ displaystyle \ log (n)}$${\ displaystyle n}$ ${\ displaystyle 1/2}$

Riemannin zeta -toiminnon käyttäytyminen ymmärretään laajalti alueilla ja . Niiden ominaisuudet ovat kuitenkin suurelta osin tuntemattomia kriittisessä kaistassa, ja niistä spekuloidaan merkittävästi. Tämä koskee muun muassa kysymyksiä asymptoottisesta kasvusta kuvitteellisessa suunnassa ja nollapisteen jakautumisesta, mikä on niin tärkeää lukuteorian kannalta. Sikäli kuin tiedämme tänään, nauhan zeta -toiminto kuvaa olennaisesti kaaosta . Nollien arvot eivät ainoastaan ​​rakenna siltoja alkuluvuteoriaan, vaan todennäköisesti myös nykyaikaiseen kvanttifysiikkaan . Muita sovellusalueita ovat todennäköisyysteoria ja automorfisten muotojen teoria (erityisesti Langlands -ohjelman alalla ). ${\ displaystyle \ operaattorinimi {Re} (t) \ geq 1}$${\ displaystyle \ operaattorinimi {Re} (t) \ leq 0}$ ${\ displaystyle 0 <\ operaattorinimi {Re} (t) <1}$${\ displaystyle 1/2 <\ operaattorinimi {Re} (t) <1}$

Vuodesta näkökulmasta algebrallinen lukuteoria , Riemannin Zeta funktio on vain erikoistapaus koko luokan ns L-toimintoja . Se vastaa triviaalimerkkiin modulo 1 kuuluvaa Dirichletin L-funktiota ja numerokenttää ( järkevät numerot ) vastaavaa Dedekind-zeta-funktiota . ${\ displaystyle \ mathbb {Q}}$

Koska Riemannin hypoteesi on äärimmäisen tärkeä lukuteorian ja sen sovellusten kannalta, Riemannin zeta -funktion aihe on edelleen intensiivisen matemaattisen tutkimuksen alue. Ratkaisevaa edistystä tehtiin matemaatikot kuten Lindelöf , Hadamard , de La Vallée poussin , Hardy , Littlewood , Selberg , Woronin ja Conrey .

Merkintä: Täysin artikkelissa viitataan imaginääriyksikköä ja Euler numero . Sitä käytetään myös usein monimutkaisena muuttujana, joka usein jaetaan. ${\ displaystyle \ mathrm {i}}$${\ displaystyle \ mathrm {e} = 2 {,} 71828 \ pistettä}$${\ displaystyle s}$${\ displaystyle s = \ sigma + \ mathrm {i} t}$

Lisäksi Landaun O -merkintää käytetään usein ilmaisemaan vikojen koko. Toimi kahdella (rajoittamattomalla) funktiolla ja sama kasvavalla argumentilla, mikä on totta , niin tämä on huomioitava. ${\ displaystyle f}$${\ displaystyle g}$${\ displaystyle \ lim _ {x \ to \ infty} f (x) / g (x) = 1}$${\ displaystyle f (x) \ sim g (x)}$

Luokittelu ilman ennakkotietoa

motivaatio

Kullekin alkuluvulle laskentatoiminto ottaa yhden askeleen äärettömän pitkiä ja korkeita portaita ylöspäin. Ennuste "käärmeitä" tasaisesti laskutoiminnon ympärillä. Hyvin suurilla arvoilla voidaan kuitenkin odottaa yhä suurempaa etäisyyttä portaikon ja ennusteen välillä.

Zeta -funktion nollat ​​korjaavat ennusteen täsmälliseen termiin. Kuvassa näkyy 100 nollaparin korjaus.

Keskiössä lukuteoria , että matematiikan, joka käsittelee ominaisuuksia luonnolliset luvut 1, 2, 3, 4 ..., ovat alkulukuja 2, 3, 5, 7, 11 ... Nämä erottuvat ominaisuuden mukaan, tarkalleen kaksi Jakajien saaminen , nimittäin 1 ja itsesi. 1 ei ole alkuluku. Eukleides pystyi jo osoittamaan, että alkulukuja on ääretön määrä, minkä vuoksi luettelo 2, 3, 5, 7, 11 ... ei koskaan lopu.

Alkuluvut ovat niin sanotusti kokonaislukujen atomeja , koska jokainen positiivinen kokonaisluku voidaan hajottaa yksiselitteisesti moninkertaisesti sellaisiksi. Esimerkiksi 21 = 3,7 ja 110 = 2,5 · 11. Tästä perusominaisuudesta huolimatta useiden vuosituhansien matematiikkahistorian jälkeen ei tiedetä yksinkertaista mallia, jonka alkuluvut ovat niiden järjestyksessä. Niiden luonne on yksi matematiikan merkittävimmistä avoimista kysymyksistä.

Vaikka sekvenssin 2, 3, 5, 7, 11 ... yksityiskohtainen ymmärtäminen ei ole mahdollista, voit etsiä kuvioita, jos laajennat näkemystäsi. Esimerkiksi ajatus siitä, että tilastollisten menetelmien avulla useiden ihmisten käyttäytymistä (esimerkiksi kulutuksen ja äänestyskäyttäytymisen suhteen) voidaan usein kuvata yllättävän tarkasti, vaikka yksittäinen henkilö on erittäin monimutkainen. Karkeasti ottaen tämä liittyy siihen tosiasiaan, että kasvavat määrät asiaankuuluvaa dataa antavat yhä luotettavampia tietoja . Kun kyseessä ovat alkuluvut, tällainen laajentuminen johtaa muun muassa kysymykseen siitä, kuinka monta alkulukua on kiinteän luvun alapuolella.

Esimerkiksi vain 4 alkulukua, nimittäin 2, 3, 5 ja 7, ovat pienempiä kuin luku 10. 50: n tapauksessa on jo 15 pienempää alkulukua, nimittäin

${\ displaystyle 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47.}$

1800 -luvun lopulla hämmästyttävän tarkka arvio alkulukujen jakaumasta voidaan todistaa alkuluvun lauseen seurauksena . 15-vuotias Gauss oletti alkuluvun lauseen jo 1700-luvulla (vuosina 1792/93). Arvio annettiin jo ennen Riemannin todistusta alkuluvun lauseesta ja se näkyy kaavana, joka mahdollistaa ennustetun arvon nopean laskemisen. Tällä kaavalla tietylle luvulle voidaan arvioida tätä lukua pienempien alkulukujen määrä kohtuullisessa ajassa. Ennustekaava muuttuu yhä tarkemmaksi prosentteina , mitä suurempi luku valitaan (mutta vaihtelevasti). Esimerkiksi se antaa ennusteen 14.97 arvolle 50 (alkulukuja on itse asiassa 15, katso yllä), mikä tarkoittaa, että virhe on 0,16 prosenttia. Se ennustaa myös noin 78 527 alkulukua alle luvun 1 000 000 - itse asiassa niitä on 78 498. Tämä vastaa 0,037 prosentin poikkeamaa.

Mahdollinen työkalu tämän kaavan todistamiseen on Riemannin zeta -funktio. Se hyödyntää sitä tosiasiaa, että se ilmaisee yksiselitteisen alkutekijäämisen lain analyysikielellä . Joten alkulukujen ominaisuudet tallennetaan piilotettuina tähän funktioon. Jos zeta -funktion tuntemus kasvaa, myös alkuluvujen tuntemus kasvaa, jopa yksityiskohtaisempien kysymysten yhteydessä. Tällä tavalla monet alkukokeet, kuten Miller-Rabin , voidaan todistaa tai parantaa Riemannin hypoteesin oletuksella .

Nollat Zeta funktio tuottaa korjaustermi on edellä mainittu kaava, joka muuntaa ne osaksi tarkka ilmaisu. Tuloksena oleva tarkka kaava tietää alkulukujen jakautumisen viimeiseen yksityiskohtaan asti. Tämä ei kuitenkaan tarkoita sitä, että alkulukuja koskevat kysymykset olisi ratkaistu: laskentatyö lisääntyy jyrkästi arvojen kasvaessa, joten tämän kaavan mukaiset käytännön laskelmat eivät ole tehokkaita. Sitä vastoin nykyaikaiset alkutestit sopivat paremmin numeeriseen tutkimukseen . Tarkka kaava kiinnostaa kuitenkin teoreettisesti: se sisältää virhemarginaalin yksinkertaisen ennusteen ja todellisen alkuluvun jakauman välillä. Oletetaan, että tämä virhe (kaikkien mahdollisuuksien rajoissa) on pienin mahdollinen. Tämän virheen tulkitseminen ei olisi niin tärkeää numeron kannalta . Pikemminkin puhdas matematiikka pyrkii selvittämään aiemmin piilotetun syyn siihen, miksi virhe (jos sovellettavissa) on mahdollisimman pieni.

Alkuluvut eivät ole vain matemaattisen perustutkimuksen aihe, vaan niillä on myös käytännön sovelluksia. Esimerkiksi erittäin suuria alkulukuja käytetään salausjärjestelmissä , kuten RSA -salauksessa .

Miten zeta -toiminto "toimii"?

Matematiikka toiminto toimii periaatteessa laskukone . Syötät funktioon arvon, joka antaa tulon tuloarvosta riippuen, ainakin teoreettisesti. Tämä tarkoittaa sitä, että funktiota ei lasketa sellaiseksi, vaan se on enimmäkseen vain aritmeettinen sääntö kaava . Yksinkertainen esimerkki funktiosta on neliöfunktio , joka kertoo syötteen itse. Kaavamaisesti tämä kirjoitetaan muodossa . Siten esimerkiksi asteen funktio määrittää arvon numerolle . Jos lasket tämän, tulos on siis . ${\ displaystyle f (x) = x ^ {2}}$${\ displaystyle -2}$${\ displaystyle (-2) ^ {2}}$${\ displaystyle 4}$${\ displaystyle f (-2) = 4}$

Periaatteessa Riemannin zeta -toiminto toimii täsmälleen kuten yllä oleva esimerkki, vain laskentasääntö on hieman monimutkaisempi. Näiden ymmärtämiseksi ääretön sarja on ymmärrettävä . (Lähentyvä) sarja on karkeasti ottaen numeroiden summa, joka ei koskaan lopu ja joka lähestyy ja lähenee numeroa. Yksinkertainen, ei-triviaali esimerkki sarjasta perustuu numeroon, jota ei ole suljettu desimaalimerkinnällä, vaan vain loputtoman jaksollisen kehityksen kautta ${\ displaystyle 1/9}$

${\ displaystyle {\ frac {1} {9}} = 0 {,} 11111111111 \ pistettä}$

voidaan kirjoittaa. Tutkitaan tarkemmin, voit nähdä, että tämä on vain summa kehrwertiger 10s valtuudet on:

${\ displaystyle {\ frac {1} {10}} + {\ frac {1} {100}} + {\ frac {1} {1000}} + \ cdots = 0 {,} 1 + 0 {,} 01 +0 {,} 001+ \ cdots = 0 {,} 111111 \ pistettä}$

Jotta äärettömän pitkä summa olisi likimääräinen arvo, on varmistettava, että kutsut muuttuvat "riittävän pieniksi".

Riemannin zeta -funktiota voidaan nyt verrata laskukoneeseen, joka muodostaa äärettömän summan kaikkien luonnonvoimien vastavuoroisista arvoista tällä eksponentilla tietylle luvulle . Tämä sääntö luetaan matemaattiseksi kaavaksi ${\ displaystyle x}$

${\ displaystyle {\ begin {aligned} \ zeta (x) & = {\ frac {1} {1 ^ {x}}} + {\ frac {1} {2 ^ {x}}} + {\ frac { 1} {3 ^ {x}}} + {\ frac {1} {4 ^ {x}}} + {\ frac {1} {5 ^ {x}}} + {\ frac {1} {6 ^ {x}}} + {\ frac {1} {7 ^ {x}}} + {\ frac {1} {8 ^ {x}}} + {\ frac {1} {9 ^ {x}}} + \ cdots \\ & = \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {x}}}. \ end {aligned}}}$.

Ymmärtääksesi tämän paremmin, harkitse syötteen esimerkkiä . Luonnollinen valtuuksia tämän eksponentti ovat neliön numerot 1, 4, 9, 16, 25 .... Tämä johtaisi zeta -laskimen tulokseen syöttöarvosta 2 riippuen ${\ displaystyle x = 2}$

${\ displaystyle \ zeta (2) = {\ frac {1} {1}} + {\ frac {1} {4}} + {\ frac {1} {9}} + {\ frac {1} {16 }} + {\ frac {1} {25}} + {\ frac {1} {36}} + {\ frac {1} {49}} + {\ frac {1} {64}} + {\ frac {1} {81}} + \ cdots.}$

On käynyt ilmi, että lausekkeet pienenevät riittävän nopeasti, joten tämä äärettömän pitkä summa lähentää mielivaltaisesti tiettyä numeerista arvoa sitä enemmän, mitä lisäät. Kokeellisesti voidaan todeta: ${\ displaystyle 1 / N ^ {2}}$

${\ displaystyle 1 = 1; \ qquad 1 + {\ frac {1} {4}} = 1 {,} 25; \ qquad 1 + {\ frac {1} {4}} + {\ frac {1} { 9}} \ noin 1 {,} 361; \ qquad 1 + {\ frac {1} {4}} + {\ frac {1} {9}} + {\ frac {1} {16}} \ noin 1 {,} 4236}$

ja jos edes miljoonas neliön numero on ${\ displaystyle 1,000,000 ^ {2} = 1 000 000 000 000}$

${\ displaystyle 1 + {\ frac {1} {4}} + {\ frac {1} {9}} + \ cdots + {\ frac {1} {1 000 000 000 000}} \ noin 1 {,} 644933.}$

Koska tähän on jo lisätty paljon termejä, voidaan olettaa, että tarkka tulos on jo melko lähellä. Leonhard Euler pystyi perustelemaan tämän, tarkka raja -arvo on numero ${\ displaystyle 1 {,} 644933}$

${\ displaystyle {\ frac {\ pi ^ {2}} {6}} = 1 {,} 644934066848226436472415 \ dotso}$.

Jossa on ympyrä numero . Vaikka Euler tiesi desimaalisekvenssin alun , hänen perustelunsa perustuivat viime kädessä matemaattisiin argumentteihin eivätkä nimenomaisiin laskelmiin, koska summa ei lopu koskaan. Siten tulon 2 zeta -toiminto antaa tuloksen . Vastaavasti tulo 3, 4 ... jne., Vastavuoroista kaikki arvot kuution numerot , BIQUAD numerot jne. On lisättävä vastaavasti ja uudet raja-arvot , ... jne. Ovat luoneet. ${\ displaystyle \ pi = 3 {,} 1415926 \ pistettä}$${\ displaystyle 1 {,} 64493406684822 \ dotso}$${\ displaystyle \ pi ^ {2} / 6}$${\ displaystyle \ zeta (3)}$${\ displaystyle \ zeta (4)}$

tarina

Toisin kuin alkuluvut tai euklidinen geometria , Riemannin zeta -funktion matemaattisen löytämisen historia on hyvin tuore. Kaikki tähän mennessä tehdyt merkittävät löydöt tästä toiminnosta on tehty viimeisten 250 vuoden aikana. Toisaalta varhainen löytö , joka liittyy tiukan ( monimutkaisen ) analyysin syntymiseen, voidaan selittää sarjan yksinkertaisuudella. Toisaalta myöhäiset tulokset voidaan selittää niiden ominaisuuksien vaikeudella.

Leonhard Euler ratkaisi Baselin ongelman noin vuonna 1735

Leonhard Euler, 1753

Eulerin nimenomaiset laskelmat alkuperäisessä De Summis Serierum Reciprocarumissa

Yksi ensimmäisistä matemaatikoista, joka käsitteli intensiivisesti ja yksityiskohtaisesti tänään määritellyn zeta -funktion edelläkävijää, oli Leonhard Euler . 1600 -luvun puolivälistä lähtien matemaatikot yrittivät löytää äärettömän sarjan tarkan rajan

${\ displaystyle 1 + {\ frac {1} {2 ^ {2}}} + {\ frac {1} {3 ^ {2}}} + {\ frac {1} {4 ^ {2}}} + {\ frac {1} {5 ^ {2}}} + \ piste}$

määrittämiseksi. Persoonallisuuksia kuten Pietro Mengoli , joka ensin muotoiltu Basel ongelma (koska se oli myöhemmin kutsutaan), mutta myös Jakob minä Bernoulli epäonnistui yrittäessään ratkaista niitä. Leonhard Euler löysi ratkaisun vasta noin vuonna 1734

${\ displaystyle 1 + {\ frac {1} {2 ^ {2}}} + {\ frac {1} {3 ^ {2}}} + \ dotsb = {\ frac {\ pi ^ {2}} { 6}} = 1 {,} 6449340668 \ pistettä}$

jossa ympyrä numero mukaan kehittämällä uusi tekniikka laskettaessa sinifunktion . Hänen aikalaisensa eivät kuitenkaan alun perin hyväksyneet tätä todistusta sen julkaisemisen jälkeen. Hän vastusti julkaisemalla vaihtoehtoisen todistuksen vuonna 1741. Luonnollisesti Euler oli pian opiskelemassa tämän tyyppisiä sarjoja ${\ displaystyle \ pi = 3 {,} 14159265 \ pistettä}$

${\ displaystyle f (n) = 1 + {\ frac {1} {2 ^ {n}}} + {\ frac {1} {3 ^ {n}}} + {\ frac {1} {4 ^ { n}}} + {\ frac {1} {5 ^ {n}}} + \ piste}$

Kiinnostunut. Hän toivoi voivansa tehdä lisää ja tärkeämpiä lausuntoja. Itse asiassa kyse ei ollut vain Baselin ongelman ratkaisemisesta. Muun muassa hän löysi kaavat

${\ displaystyle f (4) = 1 + {\ frac {1} {2 ^ {4}}} + {\ frac {1} {3 ^ {4}}} + {\ frac {1} {4 ^ { 4}}} + {\ frac {1} {5 ^ {4}}} + \ cdots = {\ frac {\ pi ^ {4}} {90}},}$

${\ displaystyle f (6) = 1 + {\ frac {1} {2 ^ {6}}} + {\ frac {1} {3 ^ {6}}} + {\ frac {1} {4 ^ { 6}}} + {\ frac {1} {5 ^ {6}}} + \ cdots = {\ frac {\ pi ^ {6}} {945}},}$

jotka julkaistiin ensimmäisen kerran vuonna 1735 teoksessaan De Summis Serierum Reciprocarum . Vaikka funktion arvot monimutkaistuvat syötteiden määrän kasvaessa, Euler laski arvon käsin

${\ displaystyle f (26) = 1 + {\ frac {1} {2 ^ {26}}} + {\ frac {1} {3 ^ {26}}} + {\ frac {1} {4 ^ { 26}}} + {\ frac {1} {5 ^ {26}}} + \ piste = = \ \ frac {1.315.862} {11.094.481.976.030.578.125}} \ pi ^ {26}.}$

Vuonna 1755 julkaistussa kirjassaan Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum hän osoittautui lopulta yleiseksi kaavaksi . Tämä osoitti, että jokainen voidaan itse asiassa aina kirjoittaa voiman järkevänä moninkertaisena . Toisaalta hän ei onnistunut oudoissa väitteissä, esimerkiksi sarjassa ${\ displaystyle f (2n)}$${\ displaystyle f (2n)}$${\ displaystyle \ pi ^ {2n}}$

${\ displaystyle f (3) = 1 + {\ frac {1} {2 ^ {3}}} + {\ frac {1} {3 ^ {3}}} + {\ frac {1} {4 ^ { 3}}} + {\ frac {1} {5 ^ {3}}} + \ piste,}$

koska mitään hänen tekniikoistaan ​​ei voitu käyttää täällä. Hän kuitenkin lasketaan arvot ja jopa useita desimaalin tarkkuudella. Hän kirjoitti myös yhtenäisesti , missä tapauksessa parillinen luku on järkevä. Siinä tapauksessa, että se on outoa, Euler epäili, se on "toiminto ". Kuitenkin Eulerin epämääräisestä muotoilusta huolimatta tätä ei ole vielä vahvistettu. Sarjan arvot parittomille argumentteille, jotka ovat suurempia kuin 1, ovat suurelta osin tuntemattomia tähän päivään asti (vuodesta 2020 lähtien), ja niistä aiheutuu lukuisia teoreettisia oletuksia.${\ displaystyle f (2n + 1)}$${\ displaystyle n = 1, \ piste, 5}$${\ displaystyle f (n) = N \ pi ^ {n}}$${\ displaystyle N}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle N}$${\ displaystyle \ log (2)}$

Euleria pidetään zeta -funktion ja alkuluvujen välisen yhteyden löytäjänä. Tästä linkistä käytetään edelleen nimitystä Euler -tuote . Teoksessaan Variae havaitsi noin infinitas -sarjan hän kirjoitti:

Euler oli heti tietoinen alkulukujen ja geometrian välisestä suhteesta ja kirjoitti:

Siitä, että harmoniset sarjat ovat toisistaan ​​poikkeavia , mikä oli jo silloin tiedossa , Euler pystyi myös päättämään Euler -tuotteesta, että kaikkien alkulukujen vastavuoroisten arvojen summalla ei ole rajallista rajaa. Tätä tulosta kutsutaan myös Eulerin lauseeksi alkuluvujen vastavuoroisten arvojen yhteenlaskemisesta .

Euler tiesi myös Riemannin myöhemmin todistaman toiminnallisen yhtälön. Teoksessaan Remarques sur un beau rapport entre les series des puissances tant directes que reciproques hän ei kuvaillut näitä matemaattisesti tarkasti:

Euler viittasi itse asiassa Dirichlet eta -funktioon , joka kuitenkin vastaa yhtä tekijää lukuun ottamatta Riemannin zeta -funktiota. Euler ei antanut tarkkaa todistusta toiminnallisesta yhtälöstä, vaan tarkisti sen vain monien arvojen osalta ja oletti sen sitten olevan yleisesti pätevä.

Dirichlet esittää alkuluvun lauseen

Zeta -funktion avulla Peter Dirichlet osoitti, että numerosarjat, kuten 1, 5, 9, 13, 17, 21 ... tai 7, 107, 207, 307, 407 ... sisältävät lukemattoman määrän alkulukuja

Vuonna 1838 matemaatikko Peter Dirichlet osallistui merkittävästi lukuteoriaan. Hän osoitti Fermatin oletuksen, jota nyt kutsutaan Dirichletscherin alkuluvuteoreemiksi . Tämä tarkoittaa sitä, että jokainen aritmeettinen edistys, jossa on positiivinen, suhteellisen alkuluku, sisältää äärettömän monta alkulukua. Esimerkiksi tässä on ja siitä seuraa, että luettelo sisältää 1, 5, 9, 13, 17 ... äärettömän monta alkulukua. ${\ displaystyle ak + b}$${\ displaystyle a, b}$${\ displaystyle a = 4}$${\ displaystyle b = 1}$

Riemannin zeta -funktion lisäksi todistuksen avain oli koko joukko muita toimintoja, jotka myös hajoavat alkuluvutuotteiksi ja muodostavat siten "suuren perheen". Vain vuosisata myöhemmin, hienompien menetelmien ansiosta, Siegel ja Walfisz ( Siegel-Walfiszin lause ) pystyivät selkeästi määrittämään Dirichletin tulokset .

Riemannin panos zeta -toimintoon

Sitä pidetään modernin zeta -funktion teorian edelläkävijänä: Bernhard Riemann

Vuonna 1859 Bernhard Riemann selvitti zeta -funktion ja Eulerin jo julkaisemassaan julkaisussa On of the number of prime number under a kind size . Suuri saavutus oli nähdä määrittelyn laajentaminen monimutkaisiin numeroihin. Vain tällä lähestymistavalla oli mahdollista saada tarkkoja tietoja alkuluvuista 2, 3, 5, 7… itse. Tämä on huomattavaa, koska alkuluvut ovat todellisia numeroita. Riemann, joka oli Carl Friedrich Gaußin oppilas , kirjoitti kymmenen sivun opinnäytetyössään Euler-tuotteen funktionaalisen tulkinnan ja arvioinnin, joka loi yhteyden alkulukujen ja zeta-funktion ei-triviaalien nollien välille. Päätulos oli kaava, joka ilman virheitä laski alkuluvut tietyn (ei-kokonaisluvun) positiivisen luvun alla. Tämä antoi hänelle täysin uuden lähestymistavan alkuluvuteoriaan.

Työssään hän vahvisti kreikan ( zeta ) funktion symboliksi ja muotoili myös Riemannin hypoteesin , joka on edelleen todistamaton ja joka esittää tärkeän lausunnon zeta -funktion nollien tarkasta sijainnista. ${\ displaystyle \ zeta}$

Bernhard Riemannin alkuperäinen teos

Vaikka artikkeli nähdään nykyään läpimurtona ja lähtökohtana nykyaikaiselle analyyttiselle teorialle zeta -funktiosta, se ei ollut läheskään innostunut matemaatikkojen piireissä. Tämä johtui pääasiassa siitä, että Riemann oli laiminlyönyt useimmissa paikoissa todisteiden esittämisen kaavoistaan. Niinpä tapahtui, että Godfrey Harold Hardy ja John Edensor Littlewood kuvailivat Riemannin työtä vain "huomattavaksi heurististen oivallusten kertymäksi". Englantilaiset matemaatikot olivat kuitenkin 1900 -luvun alussa analyyttisen lukuteorian niin jälkeenjääneitä, että Littlewood muisti ovat saaneet Riemannin hypoteesin opettajanaan vuonna 1906. Jopa Edmund Landau oli yksi lautesten -arvostelijoista artikkelin merkityksen suhteen. Vaikka hän kutsui häntä aluksi "loistavaksi ja hedelmälliseksi", hänen kiitoksensa kääntyi pian:

Detlef Laugwitz toteaa Riemannin elämäkerrassaan, että Landau antoi myös vähän tunnustusta Eulerin uraauurtavasta työstä oppikirjoissaan, koska hän pyrki arvostamaan vain teoksia, joissa kaikki yksityiskohdat oli kehitetty. Toisaalta Felix Kleinin kaltaiset matemaatikot ihailivat, että Riemann työskenteli ”suurten yleisten ideoiden kanssa” ja ”usein luotti intuitioonsa”. Tämä oli ennen kuin Carl Ludwig Siegel osoitti kartanoa tutkiessaan, kuinka laaja Riemannin analyyttinen työ zeta -funktiota kohtaan oli. Kuitenkin kartanon laskelmia oli vaikea tulkita, ja Siegelin kaliipin matemaatikko kesti rekonstruoida Riemannin ajatukset.

Siitä lähtien varhaiseen kuolemaansa asti (hän ​​kuoli 39 -vuotiaana tuberkuloosin komplikaatioihin ) Riemann ei enää työskennellyt zeta -toiminnon parissa; se oli hänen ainoa julkaisunsa numeroteoriasta. Essee vuodelta 1859 oli vain hämärä, Riemann halusi kiittää häntä siitä, että hänet hyväksyttiin Berliinin tiedeakatemiaan.

Hänen taloudenhoitaja poltti monia Riemannin muistiinpanoja hänen kuolemansa jälkeen, kunnes Göttingenin tiedekunnan henkilökunta pysäytti ne. Loput kirjoitukset annettiin hänen leskelleen ja katosivat siten moniksi vuosiksi. Tähän päivään mennessä voidaan vain spekuloida zeta -toiminnon tulevista tuloksista, jotka olisi löydetty ilman asiakirjojen osittaista tuhoamista.

1800 -luvun viimeiset vuodet

Mangoldt todistaa Riemannin pääkaavan

Vuonna 1893 matemaatikko Jacques Hadamard julkaisi paperin, johon pantiin peruskivi Riemannin työn yksityiskohtaisemman ymmärtämisen aikaansaamiseksi. Hadamard oli onnistunut osoittamaan zeta -funktion kaavan, joka sisälsi sen nollat. Tarkkaan ottaen se oli prosessi rakentaa zeta -funktio kokonaisuutena nollistaan. Riemann oletti jo tällaisen kaavan olemassaolon, mutta sitä ei ollut vielä tiukasti todistettu. Riemannin ideoiden todentamiseen se oli kuitenkin olennainen osa: Riemannin pääkaavan argumenttien peruskaavio oli ”alkulukuinen tuote (Euler) vastaan ​​nollapistetulos (Riemann / Hadamard)”. Tämä on yksi syy siihen, miksi Hans von Mangoldt kuvasi Hadamardin panosta "ensimmäisenä todellisena edistysaskeleena tällä alalla 34 vuoteen".

Hadamardin työn pohjalta Hans von Mangoldt saavutti läpimurron Riemannin pääkaavalle vasta kaksi vuotta myöhemmin, vuonna 1895. Hän kuitenkin osoitti tämän hieman muokatussa versiossa, jota pidetään nyt "luonnollisempana". Saavutuksensa kunniaksi pääkaava tunnetaan nyt nimellä Riemann von Mangoldtin kaava.

Hadamard ja De La Vallee-Poussin todistavat alkuluvun lauseen

Sen jälkeen, kun von Mangoldt oli toimittanut todisteet Riemannin pääkaavasta vuonna 1895, alkuluvun lauseen todistamiseen ei jäänyt paljon. Tämä lause kertoo, kuinka usein alkuluvut esiintyvät keskimäärin. Jäljellä oli vain osoittaa, että zeta -funktiolla ei ole nollia alueella, jolla Eulerin alkuluvutulo ”ei enää ole voimassa”. Hadamard ja belgialainen Charles-Jean de La Vallée Poussin toimittivat todistuksen itsenäisesti vuonna 1896. Tärkeitä todisteita olivat Franz Mertensin ideat ja trigonometrinen identiteetti .${\ displaystyle 3 + 4 \ cos (\ theta) + \ cos (2 \ theta) = 2 (1+ \ cos (\ theta)) ^ {2}}$

Vaikka matemaatikko maailmassa oli suurta jännitystä, oli huolta todistusmenetelmän luonnollisuudesta, joka oli vahvasti sidoksissa vaikean zeta -toiminnon ominaisuuksiin. Katsottiin outoa, että väitteen alkulukuja oli jopa vastaavan tiettyyn jakautumista juuret monimutkainen tehtävä. Albert Ingham sanoi vuonna 1932:

Lopuksi vuonna 1948 Atle Selberg ja Paul Erdös esittivät perustavanlaatuisen (toisin sanoen täysin ilman toimintoteoreettisia keinoja) todistuksen . Tässä yhteydessä "alkeellinen" ei kuitenkaan tarkoita "yksinkertaista". Ajan mittaan löydettiin paljon yksinkertaisempia funktionaalisia ja alkeellisia todisteita alkuluvulauseesta.

1900 -luvun alku

Hilbert muotoilee 23 ongelmaansa

David Hilbert muotoili 23 matemaattista tehtävää, joista kahdeksas oli Riemannin hypoteesi

David Hilbert piti luennon 8. elokuuta 2nd International Congress of Matematiikan Pariisissa vuonna 1900 . Tässä hän muotoili luettelon 23 matemaattisesta ongelmasta, jotka hänen mielestään olivat tulevan vuosisadan tärkeimpiä. Tässä vaiheessa Hilbert oli jo aikamme johtavia matemaatikkoja. Ongelma 8 oli Riemannin hypoteesi:

Hilbertin hyvä maine sai matemaatikot kamppailemaan ongelmiensa kanssa, mukaan lukien zeta -toiminto. Tähän mennessä 15 ongelmasta 23: sta katsotaan ratkaistuksi, mutta ei Riemannin hypoteesina.

Ramanujanin työ zeta -funktiosta

Hänellä oli valtava määrä tietoa zeta-toiminnosta, itseoppinut: Srinivasa Ramanujan

Hänen suurin matemaattinen löytönsä oli "Ramanujan": Godfrey Harold Hardy

Vuonna 1910 intialainen matemaatikko Srinivasa Ramanujan julkaisi artikkelin Journal of the Indian Mathematical Society -lehdessä, jossa muun muassa todettiin seuraava yhtälö:

${\ displaystyle 1 + 2 + 3 + 4 + 5 + \ dotsb = - {\ frac {1} {12}}.}$

Useimmat matemaatikot, jotka näkivät tämän yhtälön, pitivät sitä ilmeisenä hölynpölynä. Niin tapahtui, että professori Hill of University College London kirjoitti:

Hill ei kuitenkaan toiminut täysin kielteisesti ja kannusti Ramanujania jatkamaan yrittämistä. Ja niin hän lähetti tulokset suoraan joillekin Cambridgen matemaatikoille . Kaksi heistä ei kyennyt lukemaan Ramanujanin salattujen kaavojen takana olevia lausuntoja ja hylkäsi avunpyynnön. Kuitenkin, kun Ramanujan lopulta kirjoitti kirjeessään Godfrey Harold Hardylle kiinnittääkseen huomionsa hänen ideoihinsa, hän huomasi, että yhtälön arvo on arvioitu oikein , vaikka se olisi tietenkin virheellinen sen matemaattisen muodollisuuden kannalta. Tässä yhteydessä kaava oli jo Eulerin tiedossa, koska se johtuu funktionaalisesta yhtälöstä (Eulerin löytämä). Lisäksi Ramanujanin väite, että sillä on kaava, joka ennustaa melkein virheettömästi, onko tietty luku ensisijainen vai ei (Ramanujanin kaava ei käyttänyt zeta -funktion nollia) herätti paljon uteliaisuutta. Hän ei kuitenkaan esittänyt tästä todisteita toisessa kirjeessään. Littlewood totesi: ${\ displaystyle \ zeta (-1)}$${\ displaystyle \ zeta (2)}$

Alun perin yksinomaan kirjallinen vaihto huipentui Ramanujanin oleskeluun Englantiin, missä Ramanujanin ja Hardyn kaksikko kehittyi yhdeksi historian tuottavimmista ja poikkeuksellisimmista matemaattisista vastaavuuksista.

Arvioidessaan muun muassa George E.Andrewsin ja Bruce Berndtin Ramanujanin päiväkirjoja, Ramanujanin lukuisat ajatukset Riemannin zeta -toiminnasta paljastettiin. Niinpä hän löysi itsenäisesti Eulerin kaavan , Euler-tuotteen sekä lukuisia loputtomia sarjoja ja integraaleja, jotka sisältävät zeta-arvoja kokonaisina ja puoliksi kokonaisluvuina.${\ displaystyle \ zeta (2n)}$

Riemannin perintö

Pystyi valmistamaan suuria osia Riemannin säilyneistä tietueista jälkipolville: Carl Ludwig Siegel

Viisikymmentä vuotta Riemannin kuoleman jälkeen muutamia polttamattomia sivuja ilmestyi uudelleen. Richard Dedekind , Riemannin kollega, oli saanut joitakin sivuja kartanosta Riemannin vaimolta Eliseltä ja tallentanut osan niistä Göttingenin kirjastoon. Kun matemaatikko Erich Bessel-Hagen löysi kirjoitukset vuonna 1926 ja epäonnistui yrittäessään tulkita sekavia tietueita, asiakirjat menivät Carl Ludwig Siegelille . Hän oli hämmästynyt Riemannin ajatusten syvyydestä zeta -toiminnasta. Tämä myös mitätöi suuren osan Riemannin alkuperäistä työtä koskevasta kritiikistä, koska muistiinpanot osoittivat, että Riemannin väitteet perustuivat perusteellisiin laskelmiin. Siegel valitti kuitenkin myös kaaoksesta muistiinpanoissa:

Siegel huomasi, että Riemann oli laskenut vähintään kolme ei-triviaalia nollaa zeta-funktiosta suhteellisen tarkasti käyttäen vain käsinkirjoitettuja laskelmia. Tähän käytettyä kaavaa kehitti Siegel, joka julkaistiin vuonna 1932 ja jota on myös kutsuttu Riemann-Siegelin kaavaksi siitä lähtien .

Vuodesta 1945 tähän päivään

Tietokonekaudella

Riemannin zeta -funktion tutkimuksessa tietokoneita käytetään pääasiassa tarkistamaan Riemannin hypoteesin oikeellisuus mahdollisimman monelle nollalle. Vaikka kaikki laskelmat ovat numeerisia menetelmiä , ne osoittavat täsmällisesti eikä vain likimääräisesti, että tutkitut nollat ​​ovat kriittisellä suoralla.

Jo vuonna 1936 matemaatikko Edward Charles Titchmarsh , joka työskenteli Oxfordissa , laski ensimmäiset 1041 ei-triviaalia nollaa zeta-toiminnolla koneella, joka oli alun perin suunniteltu tähtitieteellisiin laskelmiin. Vuonna 1953 näitä laskelmia jatkoi Alan Turing . Hänen menetelmänsä on edelleen käytössä. Tietokonetta käytettiin ensimmäistä kertaa.

1980 -luvun alusta lähtien tietokoneista tuli yhä tehokkaampia. Jo vuonna 1979 Amsterdamin ryhmä, jota johtivat Herman te Riele ja Richard P.Brent, tarkisti 200 miljoonaa nollaa (hieman myöhemmin he nostivat laskunsa 300 miljoonaan) - kaikki olivat kriittisellä linjalla. Näin tehdessään he olivat ristiriidassa Don Zagierin ennustuksen kanssa , joka oli sanonut, että olisi ”ihme”, jos ne kaikki olisivat edelleen kriittisellä linjalla. Näin tehdessään Zagier viittasi teoreettisiin syihin, jotka vahvistivat muutaman ensimmäisen tuhannen suoran suoran nollan aseman, mutta jotka tulkittiin heikommaksi - ja lopulta puhuen sitä vastaan ​​- lukujen kasvamiseksi.

Vuoteen 2005 asti hajautetut tietokoneet tarkastivat ensimmäiset 900 miljardia nollaa osana ns. ZetaGrid-projektia . Samaan aikaan Xavier Gourdon laski Patrick Demichelin tuella ensimmäiset 10 biljoonaa ( ) nollaa. Kaikki olivat kriittisellä tiellä. ${\ displaystyle 10 ^ {13}}$

Numeroteoria kohtaa kvanttifysiikan

Osallistui aluksi tahattomasti keskusteluun Dysonin kanssa Sarvadaman Chowlan kehotuksesta : Hugh Montgomery

Freeman Dyson, jota pidetään yhtenä 1900 -luvun johtavista asiantuntijoista satunnaisten matriisien alalla

Vuonna 1972 sattunut keskustelu fyysikon Freeman Dysonin ja matemaatikon Hugh Montgomeryn välillä paljasti aiemmin huomaamattoman yhteyden kvanttifysiikan ja lukuteorian välillä. Keskustelun aiheena olivat Riemannin zeta -funktion nollat. Montgomeryn ehdottamassa jakaumassa Dyson tunnisti etäisyydet Hermitianin satunnaismatriisien ominaisarvoparien välillä . Kvanttifyysikot käyttävät niitä ennustaakseen raskaan atomin ytimen energiatasot , kun sitä säteilytetään matalaenergisillä neutroneilla . Kun Montgomery tarkasteli etäisyyksiä atomitason erbiumin , jaksollisen taulukon 68. elementin energiatasojen välillä , hän näki hämmästyttävän samankaltaisuuden. Yleinen sopimus kriittisen suoran nollan sijaintien tietyn osan ja kokeellisesti määritettyjen energiatasojen välillä osoitti suurta merkitystä .

Laajalla tietokoneiden käytöllä Andrew Odlyzko vahvisti Montgomeryn oletuksen nollapisteestä . Luvut puhuivat Montgomeryn olettaman puolesta. Vuonna 1987 Odlyzko julkaisi tulokset.

Vahvista todisteista huolimatta joitakin tuloksia tarkasteltiin epäilevästi. Heräsi kysymys, oliko tämä edistynyt puhtaassa matematiikassa . Siten määrä teoreetikko kommentoi Peter Sarnak of Princeton :

Fyysikko Michael Berryn opiskelija Jonathan Keating esitti pian useita teoreettisia sovelluksia. Berry oli aiemmin käsitellyt alkulukujen ja kvanttifysiikan välisiä yhteyksiä (erityisesti yhteyksiä kvanttikaosiin ). Mutta se oli lopulta Keating ja hänen tohtorikoulutettava Nina Snaith kuka, joiden avulla tilastollisia menetelmiä (joita usein käytetään kvanttifysiikan), perustaa tarkka kaava keskimääräistä käyttäytymistä toimivallan itseisarvojen Zeta funktio kriittistä suoraa linjaa pitkin. Nämä keskiarvot ovat tärkeitä lukuteoriassa ja niillä on monia sovelluksia esimerkiksi Dirichletin jakajaongelmaan . Muutama minuutti ennen Keatingin esittelyä tuloksista hän ja Snaith olivat "testanneet" kaavan liitutaululla tarkistamalla, ennustettaisiinko jo vaivalloisesti kehitetty tulos oikein. Keatingin ja Snaithin lähestymistavassa, jota Atle Selberg kiitti muun muassa , oli erityistä se, että he tulkitsivat alkuluvut satunnaismuuttujiksi , ts. Kolikonheiton tuloksiksi . Sarnak oli samaa mieltä siitä, että ilman tätä outoa lähestymistapaa tällaista oletusta zeta -toiminnasta ei olisi voitu selvittää.

Montgomeryn parikorrelaatio -olettamus ja zeta -hetkien asymptoottinen käyttäytyminen ovat intensiivisen tutkimuksen kohteena tähän päivään asti.

Riemannin hypoteesi tähän päivään

Kun Hilbert oli laittanut Riemannin hypoteesin ongelmalistalleen, se herätti lukuisten matemaatikkojen kiinnostuksen. Mutta tähän päivään mennessä ongelma on osoittautunut erittäin vaikeaksi.

Sen jälkeen, kun Atle Selberg oli osoittanut vuonna 1942, että positiivinen osa nollista on oltava kriittisellä suoralla, todellinen kilpailu tämän osuuden koosta kehittyi. Norman Levinson osoitti, että hyvä kolmasosa täyttää oletuksen, ja Brian Conrey osoitti vuonna 1989, että se on jopa hyvä 40 prosenttia. Se, johtavatko nämä menetelmät lopulta ratkaisuun, on kiistanalainen. Ei edes sellainen todiste, että "100 prosenttia" (asymptoottisessa mielessä) nollasta noudattaa olettamusta, olisi täysin tehokas, koska nollien määrä on äärettömän suuri. Samanlaisia ​​huolenaiheita esiintyy pyrkimyksissä optimoida nolla-alueet.

Fields -mitalin saaja Stephen Smale julkaisi oman luettelonsa 18 ongelmasta - jotka on kirjoitettu Hilbertin merkityksessä - vuonna 1998. Tehtävä numero 1 on Riemannin hypoteesi. Tähän mennessä vain muutama Smale -luettelon ongelma on ratkaistu (katso Smale -ongelmat ).

Riemannin hypoteesi sai lisää mainetta, kun Clay Mathematics Institute (CMI) otti sen 2000: n vuosituhannen ongelmien luetteloon . Vakuuttavia todisteita varten on jaettu miljoonan Yhdysvaltain dollarin palkintoraha.

Määritelmä ja perusmuodot

Dirichlet -sarja

Zeta -funktio määritellään kirjallisuudessa usein sen esittämisellä Dirichlet -sarjana .

Ja kompleksiluvut jonka todellinen osa on suurempi kuin 1, Zeta funktio on määritelty dirichlet'n sarja${\ displaystyle s}$

${\ displaystyle \ zeta (s): = \ summa _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {s}}} = 1 + {\ frac {1} {2 ^ { s}}} + {\ frac {1} {3 ^ {s}}} + {\ frac {1} {4 ^ {s}}} + {\ frac {1} {5 ^ {s}}} + {\ frac {1} {6 ^ {s}}} + {\ frac {1} {7 ^ {s}}} + \ piste, \, \, \, \, \, \, \, \, \ , n ^ {s}: = \ exp (s \ log (n)).}$

Kuten voidaan osoittaa äärettömän sarjan integraalikriteerin avulla , tämä sarja on ehdottomasti lähentynyt tietyllä alueella . Lisäksi lähentyminen on tasaista kompakteilla osajoukoilla, minkä vuoksi esitetty funktio on holomorfinen Weierstrassin lauseen mukaan . Koska harmoniset sarjat eroavat toisistaan , tämä esitys on virheellinen kaikille kompleksiluvuille, joiden todellinen osa on pienempi tai yhtä suuri kuin 1 . Tämä on erityisen ilmeistä negatiivisten argumenttien osalta, esimerkiksi jos yritettiin arvioida Dirichlet -sarjan zeta -funktiota . Sitten yksi olisi ${\ displaystyle s = -1}$

${\ displaystyle {\ begin {aligned} \ zeta (-1) & = {\ frac {1} {1 ^ {- 1}}} + {\ frac {1} {2 ^ {- 1}}} + { \ frac {1} {3 ^ {- 1}}} + {\ frac {1} {4 ^ {- 1}}} + {\ frac {1} {5 ^ {- 1}}} + {\ frac {1} {6 ^ {- 1}}} + {\ frac {1} {7 ^ {- 1}}} + \ pisteb \\ & = 1 + 2 + 3 + 4 + 5 + 6 + 7 + \ piste \ \ loppu {kohdistettu}}}$

ja tällä sarjalla ei tietenkään ole rajallista rajaa.

Siitä huolimatta Dirichlet-sarjaa käytetään perusmääritelmänä sen yksinkertaisuuden ja lukuteoreettisen merkityksen vuoksi (katso Euler-tuote). By analyyttinen jatkaminen (katso jäljempänä) on kohtuullinen laskenta kaikille kompleksiluvut kanssa mahdollista. Tällä tavalla voidaan antaa esimerkiksi arvoja, kuten merkitys . ${\ displaystyle s}$${\ displaystyle s \ neq 1}$${\ displaystyle \ zeta (-1)}$${\ displaystyle \ zeta (-1) = - 1/12}$

Euler tuote

Zeta -funktion olennainen ominaisuus on sen yhteys alkulukuihin . Euler , joka löysi ensin tämän kontekstin, katsoi myöhemmin nimettyään Euler -tuotteeksi kaikille, joilla oli voimassa:${\ displaystyle s \ in \ mathbb {C}}$${\ displaystyle \ operaattorinimi {Re} (s)> 1}$

${\ displaystyle \ zeta (s) = {\ frac {1} {\ left (1 - {\ frac {1} {2 ^ {s}}} \ right) \ left (1 - {\ frac {1} { 3 ^ {s}}} \ oikea) \ vasen (1 - {\ frac {1} {5 ^ {s}}} \ oikea) \ cdots}} = \ prod _ {p \ {\ text {prime number} }} {\ frac {1} {1 - {\ frac {1} {p ^ {s}}}}} = \ prod _ {p \ {\ text {prime number}}} \ left (1 + {\ frac {1} {p ^ {s}}} + {\ frac {1} {p ^ {2s}}} + {\ frac {1} {p ^ {3s}}} + \ piste \ oikea).}$

Se vastaa täsmälleen Dirichlet -sarjaa, ja jotkut kirjoittajat käyttävät sitä määritelmänä. Jokainen tuotteen tekijä edustaa geometrista sarjaa, joka on muodostettu arvon päälle , kun taas koko tuote ulottuu kaikkien alkuluvujen yli . Euler -tuote on hämmästyttävä, koska alkulukuja on erittäin vaikea sovittaa analyyttisiin lausekkeisiin niiden kaoottisen jakautumisen vuoksi. Mutta se edustaa yllättävän yksinkertaista identiteettiä "kaoottisten alkuluvujen" ja tunnetun sarjan välillä. ${\ displaystyle \ texttyle \ sum q ^ {n}}$${\ displaystyle q = p ^ {- s}}$${\ displaystyle p}$

Euler -tuote lähenee välttämättä tarkasteltavaa aluetta . Koska mikään tekijä ei ota arvoa 0, suora seuraus on, että zeta -funktiolla ei ole nollia tällä alueella. Käyttämällä identiteettiteoriaa Dirichlet -sarjalle voidaan osoittaa, että Euler -tuote ja aritmeettinen peruslause vastaavat toisiaan. Siksi sitä kutsutaan joskus sen analyyttiseksi versioksi .${\ displaystyle \ operaattorinimi {Re} (s)> 1}$

Avulla Euler tuotteen Zeta funktio, todiste Euclid lauseen voidaan annetaan kanssa analyyttisiä menetelmiä. Eukleidesin lause sanoo, että alkulukuja on oltava ääretön määrä, ja Aleksandrian Eukleides todisti noin 300 vuotta ennen Kristusta . Jos oletetaan, että alkulukuja on vain äärettömän paljon, seuraava pätee

${\ displaystyle \ zeta (1) = \ prod _ {p \ {\ text {prime number}}} {\ frac {1} {1 - {\ frac {1} {p}}}} <\ infty,}$

mikä on ristiriidassa harmonisten sarjojen hajonnan kanssa . Yhtä huomionarvoista on väite kaavasta

${\ displaystyle \ prod _ {p \ {\ text {prime number}}} {\ frac {1} {1 - {\ frac {1} {p ^ {2}}}}} = {\ frac {\ pi ^ {2}} {6}}.}$

Kun äärellinen määrä alkulukuja, vasen puoli olisi järkevä luku , mutta oikea puoli on irrationaalinen ympyrän luvun ylittymisen vuoksi .

Mellinin muutos

Dirichlet -sarjan ja Euler -tuotteen määritelmän mukaan zeta -funktion tärkein ja tärkein esitys on virheellisen integraalisen lausekkeen avulla . Tämä esitys tulee esiin myös suoraan Dirichlet -sarjasta.

Tämä esitys perustuu Eulerin integroituun esitykseen gammafunktiosta

${\ displaystyle \ Gamma (s) = \ int \ limits _ {0} ^ {\ infty} \ mathrm {e} ^ {- x} x ^ {s-1} \ mathrm {d} x,}$

josta sen jälkeen, kun substituution kanssa ja jako jälkeen lisäämällä jopa molemmin puolin ilmaisun ${\ displaystyle x = tn}$${\ displaystyle n = 1,2,3, \ piste}$${\ displaystyle n ^ {s}}$

${\ displaystyle \ zeta (s) \ Gamma (s) = \ summa _ {n = 1} ^ {\ infty} \ int \ limits _ {0} ^ {\ infty} \ mathrm {e} ^ {- nt} t ^ {s-1} \ mathrm {d} t = \ int \ limits _ {0} ^ {\ infty} {\ frac {t ^ {s-1}} {\ mathrm {e} ^ {t}- 1}} \ mathrm {d} t}$

tulee esiin. Tämä esitys koskee luonnollisesti vain puolitasoa . Toinen kiinteä esitys on myös tunnetaan Mellin muunnos on . Summan ja integraalin mahdollinen vaihto voidaan perustella absoluuttisella lähentymisellä ja Lebesguen lauseella . Liittyvä muoto on ${\ displaystyle \ zeta (s) \ Gamma (s)}$ ${\ displaystyle \ {s \ in \ mathbb {C} \ mid \ operaattorinimi {Re} (s)> 1 \}}$${\ displaystyle \ zeta (s) \ Gamma (s)}$${\ displaystyle {\ tfrac {1} {\ mathrm {e} ^ {t} -1}}}$

${\ displaystyle \ pi ^ {- s / 2} \ Gamma \ vasen ({\ frac {s} {2}} \ oikea) \ zeta (s) = {\ frac {1} {2}} \ int \ limits _ {0} ^ {\ infty} (\ vartheta (0, \ mathrm {i} t) -1) t ^ {s / 2-1} \ mathrm {d} t}$

kanssa Jacobin theeta toiminto (a modulaarinen muodossa puoli koko paino).

Zeta -funktion esittäminen gammafunktion ja Mellin -muunnoksen avulla on siksi keskeistä, koska se on lähtökohta zeta -funktion analyyttiselle jatkamiselle . Sitä voidaan myös käyttää johdetuilla ominaisuuden toiminnallinen yhtälöt ja suhde teorian modulimuoto . ${\ displaystyle {\ tfrac {1} {\ mathrm {e} ^ {t} -1}}}$

Analyyttisen jatkamisen menetelmät

Monimutkainen kaavio alueella
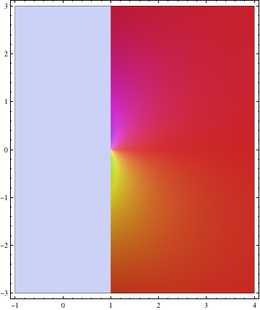
−1 <Re ( s ) <4 ja −3 <Im ( s ) <3 funktion arvojen värillä : Dirichlet-sarja, Euler-tuote ja Mellin-muunnos lähentyvät vain oikeaa puolitasoa, joka on siirretty 1: llä . Et voi näyttää zeta -toimintoa harmaalla alueella.

Monimutkainen kaavio −1 <Re ( s ) <4 ja −3 <Im ( s ) <3 funktion arvojen värillä : Vertailun vuoksi: analyyttinen jatko. Niiden arvot sopivat oikealla puolitasolla, joka on siirretty yhdellä yllä olevan kuvan kanssa. Kuitenkin ne on yleensä arvot kaikille kanssa .${\ displaystyle s}$${\ displaystyle s \ neq 1}$

Zeta -funktio, joka alun perin määritettiin vain kompleksiluvuille , voidaan laajentaa täysin holomorfiseksi funktioksi. Tämä tosiasia saattaa tuntua aluksi epätavalliselta, koska sen Dirichlet -sarja ei enää lähentynyt monissa paikoissa. Itse asiassa Dirichlet -sarja (kuten Euler -tuote ja Mellin -muunnos vastaavuussyistä) ei kuitenkaan ole saatavilla kaikkialla zeta -funktion määrittämiseksi. ${\ displaystyle \ operaattorinimi {Re} (s)> 1}$${\ displaystyle \ mathbb {C} \ setminus \ {1 \}}$

Tässä vaiheessa zeta -funktiolla on varmasti määritelmävaje, koska harmoninen sarja seuraa hajontaa${\ displaystyle s = 1}$

${\ displaystyle \ lim _ {\ sigma \ to 1 ^ {+}} \ summa _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {\ sigma}}} = \ infty.}$

Joten se kasvaa tahdosta kullakin aikavälillä . Samalla tämä aukko muodostaa luonnollisen esteen Dirichlet -sarjan lähentymiselle, mikä seuraa Dirichlet -sarjan abscisseja koskevista säännöistä : tarkasteltavalla Dirichlet -sarjalla on lähentymisabsissi . ${\ displaystyle (1,1+ \ varepsilon)}$${\ displaystyle \ sigma _ {c} = 1}$

Analyyttinen jatkaminen ja alueen läpi sarjan määritellyn holomorphic toiminto on on suurempi pinta-ala holomorphic toiminto kaikki ottelunsa tämän. Mukaan identiteetin lause varten holomorphic toimintoja , tällaista jatkoa on aina yksilöllisesti määritetään. Tämä tarkoittaa, että kaikki zeta -funktion arvot laajennetulla alueella ovat jo Dirichlet -sarjan määrittämiä, vaikka tässä se ei enää lähene kaikissa kohdissa. ${\ displaystyle H: = \ {s \ in \ mathbb {C} \ mid \ operaattorinimi {Re} (s)> 1 \}}$${\ displaystyle \ texttyle \ summa 1 / n ^ {s}}$ ${\ displaystyle H \ subsetneq D}$ ${\ displaystyle H}$${\ displaystyle D}$

Dirichlet -sarjan muunnokset ja Eulerin sarjan muutos

Vaikka ei ole olemassa rakentavaa menetelmää kaavojen antamiseksi analyyttisten jatkeiden laskemiseksi hyvin yleiselle tapaukselle, ei ole vaikeaa löytää sitä zeta -funktiolle Dirichlet -sarjan yksinkertaisuuden vuoksi . Tämä osoittautuu erityisen helpoksi rei'itetylle puolitasolle ${\ displaystyle \ texttyle \ summa 1 / n ^ {s}}$

${\ displaystyle D = \ {s \ in \ mathbb {C} \ mid \ operaattorinimi {Re} (s)> 0, s \ neq 1 + 2 \ pi \ mathrm {i} m / \ log 2, m \ in \ matematiikka {Z} \}}$

seuraavan havainnon avulla:

${\ displaystyle (1-2 ^ {1-s}) \ zeta (s) = \ summa _ {n = 1} ^ {\ infty} {\ frac {(-1) ^ {n-1}} {n ^ {s}}} = 1 - {\ frac {1} {2 ^ {s}}} + {\ frac {1} {3 ^ {s}}} - {\ frac {1} {4 ^ {s }}} + {\ frac {1} {5 ^ {s}}} - {\ frac {1} {6 ^ {s}}} + {\ frac {1} {7 ^ {s}}} - { \ frac {1} {8 ^ {s}}} + {\ frac {1} {9 ^ {s}}} - \ piste.}$

Oikealla olevan rivin on osoitettu lähentyvän puolitasossa holomorfiseksi funktioksi, ja sitä kutsutaan joskus kirjallisuudessa Dirichlet-etafunktioksi . Tämä mahdollistaa zeta -toiminnon jatkamisen täysin holomorfiseksi funktioksi. Aukko on suljettu tekijän avulla ja sen on sen vuoksi oltava ensimmäisen kertaluvun napa . Jäännösarvo Zeta funktio on 1 siinä, mikä tarkoittaa sitä, että:${\ displaystyle \ {s \ in \ mathbb {C} \ mid \ operaattorinimi {Re} (s)> 0 \}}$ ${\ displaystyle \ eta (s)}$${\ displaystyle D}$${\ displaystyle s = 1}$${\ displaystyle 1-2 ^ {1-s}}$

${\ displaystyle \ lim _ {s \ to 1} \, (s-1) \ zeta (s) = 1.}$

Toisaalta kaikki numerot, joilla on , ovat nostettavia singulaarisuuksia , koska silloin tämä näkyy parhaiten osittaisen summauksen avulla : Seuraava koskee kaikkia${\ displaystyle s_ {m} = 1 + 2 \ pi \ mathrm {i} m / \ log 2}$${\ displaystyle m \ not = 0}$${\ displaystyle \ eta (s_ {m}) = 0.}$${\ displaystyle x> 3}$

${\ displaystyle \ summa _ {n \ leq x} {\ frac {(-1) ^ {n}} {n ^ {s_ {m}}}} = 2 ^ {1-s_ {m}} \ summa _ {n \ leq x / 2} {\ frac {1} {n ^ {s_ {m}}}} - \ summa _ {n \ leq x} {\ frac {1} {n ^ {s_ {m}} }} = - \ summa _ {x / 2 <n \ leq x} {\ frac {1} {n ^ {s_ {m}}}} = O \ vasen ({\ frac {1} {x}} \ oikein).}$

Monet menetelmät soveltuvat nyt alueen edelleen holomorfiseen laajentamiseen, mutta ne kaikki edustavat samaa toimintoa identiteettiteorian mukaan. Yksi näistä tarjoaa Eulerin sarjan muunnoksen soveltamisen ylempiin vuorotteleviin sarjoihin. Tämä antaa sinulle Konrad Knoppin julkaiseman sarjan identiteetin , joka on täysin määritelty ${\ displaystyle \ mathbb {C} \ setminus \ {1 + 2 \ pi \ mathrm {i} m / \ log 2 \ mid m \ in \ mathbb {Z} \}}$

${\ displaystyle \ zeta (s) = {\ frac {1} {1-2 ^ {1-s}}} \ summa _ {n = 0} ^ {\ infty} {\ frac {1} {2 ^ { n + 1}}} \ summa _ {k = 0} ^ {n} (- 1) ^ {k} \ {n \ valitse k} \ {\ frac {1} {(k + 1) ^ {s} }}.}$

Tämän todisti vuonna 1930 Helmut Hasse . Tämän vuoksi jatkossa ei ole enää aukkoja tai pylväitä. Tämä johtaa lopulta holomorfismiin . ${\ displaystyle \ mathbb {C} \ setminus \ {1 \}}$

Euler-Maclaurin-molekyylikaava

Toinen tapa määrittää analyyttinen jatko on Euler-Maclaurin-empiirinen kaava . Tämä ilmaisee erillisiä summia nimenomaisesti integraalilaskennan kielellä, ja sen antaa yleensä:

${\ displaystyle {\ begin {aligned} \ summa _ {n = N + 1} ^ {M} f (n) = & \ int \ limits _ {N} ^ {M} f (x) \, dx + { \ frac {f (M) -f (N)} {2}} + \ summa _ {k = 1} ^ {\ lfloor p / 2 \ rfloor} {\ frac {B_ {2k}} {(2k)! }} (f ^ {(2k-1)} (M) -f ^ {(2k-1)} (N)) + \\ & + (-1) ^ {p + 1} \ int \ limits _ { N} ^ {M} f ^ {(p)} (x) {\ frac {\ mathrm {B} _ {p} (x- \ lfloor x \ rfloor)} {p!}} \, \ Mathrm {d } x. \ loppu {tasattu}}}$

Tässä on funktio, joka voidaan erottaa vähintään kerran aikavälillä ja luonnollinen luku. Se tarkoittaa myös Bernoullin polynomeja ja kokonaislukuosaa .${\ displaystyle f}$${\ displaystyle] N, M [}$${\ displaystyle p}$${\ displaystyle p \ geq 1}$${\ displaystyle \ mathrm {B} _ {\ nu} (x)}$${\ displaystyle \ lfloor x \ rfloor}$${\ displaystyle x}$

Kanssa , ja niin seuraa${\ displaystyle f (x) = x ^ {- s}}$${\ displaystyle N> 0}$${\ displaystyle M \ to \ infty}$

${\ displaystyle \ zeta (s) = \ summa _ {n = 1} ^ {N-1} {\ frac {1} {n ^ {s}}} + {\ frac {N ^ {1-s}} {s-1}} + {\ frac {1} {2}} N ^ {- s} + \ summa _ {r = 1} ^ {\ lfloor p / 2 \ rfloor} {\ frac {B_ {2r} } {(2r)!}} S (s + 1) \ cdots (s + 2r-2) N ^ {-s-2r + 1} + R_ {p} (s).}$

Jäljellä oleva aika on annettu

${\ displaystyle R_ {p} (s) = - {\ frac {s (s + 1) \ cdots (s + p -1)} {p!}} \ int \ limits _ {N} ^ {\ infty} \ mathrm {B} _ {p} (x- \ lfloor x \ rfloor) x ^ {- sp} \ mathrm {d} x,}$

ja yhtyy koko puolitasossa (tasaisesti kompakteilla osajoukoilla). Siksi tämä kaava edustaa zeta-funktion holomorfista jatkoa puolitasossa.Jos päästetään kohti äärettömyyttä, tuloksena on holomorfinen lauseke kokonaisuudessaan .${\ displaystyle \ operaattorinimi {Re} (s)> 1-p}$${\ displaystyle \ operaattorinimi {Re} (s)> 1-p}$${\ displaystyle p}$${\ displaystyle \ mathbb {C} \ setminus \ {1 \}}$

Monimutkainen kaavio funktioarvojen värjäyksellä : Alkuperäinen kuva näyttää Dirichlet-sarjan lähentymistilanteen otteessa −18 <Re ( s ) <8 ja −8 <Im ( s ) <8. Euler-Maclaurin summakaavan kautta , lisäämällä verkkotunnuksen parametria voidaan aina laajentaa yhdellä negatiiviseen todelliseen suuntaan. Kaavio näyttää tämän laajennuksen ensimmäisille parametreille . Tämän periaatteen mukaan funktio voidaan laskea mille tahansa arvolle (paitsi 1) ja yksi saa siten jatkoa kokonaisuudelle .${\ displaystyle p}$${\ displaystyle p = 1, \ pisteitä, 19}$${\ displaystyle \ zeta (s)}$${\ displaystyle s}$${\ displaystyle \ mathbb {C} \ setminus \ {1 \}}$

Jos esimerkiksi käytetään , tuloksena on esitys, joka usein mainitaan kirjallisuudessa ${\ displaystyle p = 1}$

${\ displaystyle \ zeta (s) = {\ frac {s} {s -1}} + s \ int \ limits _ {1} ^ {\ infty} {\ frac {\ lfloor x \ rfloor -x} {x ^ {s + 1}}} \, \ mathrm {d} x,}$

joka on voimassa.${\ displaystyle \ operaattorinimi {Re} (t)> 0}$

Integrointi Hankelin muodon kautta

Monimutkainen kaavio funktion arvojen värillä : Funktiolla on yksikköpiste . Äkillisen värinmuutoksen vuoksi positiivinen todellinen akseli voidaan nähdä selvästi epäjatkuvuusviivana. Hankelin muodon kulku piirretään sisään ja integraalilla on arvo .${\ displaystyle z ^ {11/2} / (\ mathrm {e} ^ {z} -1)}$${\ displaystyle z = 0}$${\ displaystyle r = 3}$${\ displaystyle -2 \ Gamma (13/2) \ zeta (13/2) \ noin -582 {,} 6832}$

Monimutkainen kaavio funktion arvojen värillä : Kokonaisluvuille Hankelin ääriviivat voidaan piirtää yhteen ympyrän muodostamiseksi. Tässä on esimerkki .${\ displaystyle s}$${\ displaystyle s = 6}$

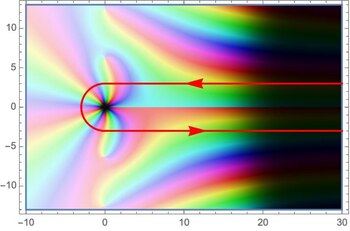
Zeta -funktion esitykseen Mellin -muunnoksen avulla liittyy läheisesti funktion esitys käyrän integraalin avulla . Tätä käytti Riemann itse jatkamaan zeta -toimintoa kompleksitasossa. Toiminto on holomorfinen eri alueilla riippuen logaritmin haaran valinnasta. Että Hankel muodon (erityinen integraatio polku) on edullista sulkea suora viiva alueelta kautta: ${\ displaystyle \ texttyle f (s; z) = z ^ {s -1} / (\ mathrm {e} ^ {z} -1)}$${\ displaystyle [0, \ infty [}]$

${\ displaystyle {\ frac {z ^ {s -1}} {\ mathrm {e} ^ {z} -1}} = {\ frac {\ mathrm {e} ^ {\ pi \ mathrm {i} (s -1) + \ log (-z) (s-1)}} {\ mathrm {e} ^ {z} -1}}.}$

Nyt funktio määritellään käyrän integraaliksi . Valittu käyrä tulee , kulkee etäisyydellä todellisesta suorasta, pyörii alkupisteen ympäri puoliympyrässä ja ulottuu sitten taas etäisyydelle todellisen suoran alapuolelle kohti : ${\ displaystyle \ pi> r> 0}$${\ displaystyle I (s)}$${\ displaystyle f (z)}$${\ displaystyle C_ {r}}$${\ displaystyle + \ infty}$${\ displaystyle r}$${\ displaystyle r}$${\ displaystyle + \ infty}$

${\ displaystyle I (s) = \ int _ {C_ {r}} {\ frac {z ^ {s -1}} {\ mathrm {e} ^ {z} -1}} \ mathrm {d} z. }$

Koska yhtenäinen lähentyminen kompakti settiä on koko funktio . Jos valitset nyt , voit vetää silmukan yhteen haluamallasi tavalla ja saat Mellin -muunnoksen ${\ displaystyle \ mathbb {C}}$${\ displaystyle I (s)}$${\ displaystyle \ operaattorinimi {Re} (s)> 1}$${\ displaystyle \ texttyle | f (s; z) | \ ll r ^ {\ sigma -2}}$

${\ displaystyle I (s) = \ lim _ {r \ to 0} (\ mathrm {e} ^ {2 \ pi \ mathrm {i} s} -1) \ int \ limits _ {r} ^ {\ infty } {\ frac {t ^ {s -1}} {\ mathrm {e} ^ {t} -1}} \ mathrm {d} t = (\ mathrm {e} ^ {2 \ pi \ mathrm {i} s} -1) \ Gamma (t) \ zeta (t).}$

Tämä johtaa kaavaan lisälauseella

${\ displaystyle \ zeta (s) = {\ frac {\ mathrm {e} ^ {- \ pi \ mathrm {i} s}} {2 \ pi \ mathrm {i}}} \ Gamma (1-s) I (s).}$

On sitten holomorfinen rei'itetyn nauhan sisällä . Tämä mahdollistaa Hankelin ääriviivan vetämisen yhteen muodostaen ympyräkäyrän muuttamatta integraalin arvoa. Tämä mahdollistaa sen, että arvot kokonaisille numerot voidaan laskea nopeasti käyttäen jäljellä lauseen . Tästä seuraa muun muassa ${\ displaystyle s \ in \ mathbb {Z}}$${\ displaystyle f (s; z)}$${\ displaystyle \ {z \ in \ mathbb {C} \ mid -2 \ pi <\ operaattorinimi {Im} (z) <2 \ pi \} \ setminus \ {0 \}}$${\ displaystyle I (n)}$${\ displaystyle n}$

${\ displaystyle I (n) = 0}$

kaikille ja zeta-funktion arvojen läheinen suhde ei-positiivisiin kokonaisargumenteihin ja Bernoullin lukuihin. ${\ displaystyle n \ geq 2}$

Tätä esitystapaa voidaan käyttää myös funktionaalisen yhtälön suoraan johtamiseen. Käyrää muutetaan ja jäännösteoriaa käytetään.

Käytännön sovellusalueet

Käytännön kannalta merkitykselliset sovellukset on esitetty alla. Suhteita matemaattiseen ja fyysiseen perustutkimukseen löytyy alla seuraavilta alueilta:

• Analyyttinen lukuteoria
• Algebrallinen lukuteoria
• Automorfiset muodot
• geometria
• Todennäköisyysteoria ja tilastot

Nopeat alkukokeet

Alkuluku testi on algoritmi , joka testaa, onko tietty määrä on alkuluku . Jos menettely on tässä täysin naiivi, hän on laskenut uudelleen, onko yksi numeroista, jolla on jakaja . Jos mikään näistä numeroista ei jaa , sen on oltava alkuluku, koska jokainen jakaja on suurempi kuin jakaja pienempi kuin vastaava . Tämä menetelmä vaatii n. Aritmeettisia operaatioita, koska likimääräiset osamäärät on muodostettava ja arvioitava. Tämä tarkoittaa, että yksinkertaisuudestaan ​​huolimatta sen katsotaan olevan monimutkainen. ${\ displaystyle n}$${\ displaystyle 2,3, \ dots, q}$${\ displaystyle {\ sqrt {n}} \ leq q <{\ sqrt {n}} + 1}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle r}$${\ displaystyle q}$${\ displaystyle s}$${\ displaystyle q}$${\ displaystyle rs = n}$${\ displaystyle O ({\ sqrt {n}})}$${\ displaystyle q}$

Riemannin zeta -funktion nollien sijainnilla on merkitystä nopeampien alkutestien olemassaolon osoittamisessa. Olettaen yleistetyn Riemannin hypoteesin , Gary L. Miller pystyi osoittamaan vuonna 1976, että on olemassa deterministinen alkuluvutesti, joka tarkistaa vaiheittain (eli "nopeasti"), onko numero alkuluku vai ei. Termi yleistetty Riemannin hypoteesi tarkoittaa, että paitsi Riemannin zeta-funktio, myös kaikki Dirichletin L-funktiot eivät koskaan oleta argumentteja , joiden arvo on nolla. ${\ displaystyle O (\ log (n) ^ {4} \ log (\ log (\ log (n))))}$${\ displaystyle n}$${\ displaystyle s}$${\ displaystyle \ operaattorinimi {Re} (s)> 1/2}$

Vuonna 1980 Michael O.Rabin onnistui muuttamaan tämän todennäköisyyskoeksi, joka, vaikka se ei koskaan anna 100 prosentin oikeaa tulosta, on erittäin luotettava riittävän määrän vaiheiden jälkeen. Tämä toimii Riemannin hypoteesista riippumatta.

Suuria alkulukuja käytetään tietojen salaamiseen (esimerkiksi Internetissä ). Tällaisten järjestelmien turvallisuus perustuu oletukseen, että numeron esitäyttö ei ole nopeaa. RSA -salausjärjestelmä, henkilö, joka haluaa salata viestin, ottaa kaksi suurta alkulukua ja toisilleen laajalti ja muodostaa yhdistelmäluvun . Tämän avulla viestit (jos ne on aiemmin muutettu numeroiksi) voidaan nyt salata käyttämällä julkista avainta, joka on luotu osoitteista ja . Tämä avain on kaikkien saatavilla, mutta se ei anna mitään tietoa itse salausjärjestelmästä. Tietojen avulla ja julkisen viestin yksityishenkilöille voidaan sitten purkaa uudelleen, koska tietämyksen avulla ja myös "vastaava avain" voidaan luoda, mikä palauttaa tekstin . Tämä laskuri on vain yksityishenkilöiden käytettävissä ja siksi yksityinen avain . Siksi järjestelmän rikkomiseksi on tarpeen tekijä . ${\ displaystyle p}$${\ displaystyle q}$${\ displaystyle pq = N}$${\ displaystyle p}$${\ displaystyle q}$${\ displaystyle p}$${\ displaystyle q}$${\ displaystyle p}$${\ displaystyle q}$${\ displaystyle N}$

fysiikka

Vuonna fysiikka Riemannin näyttelee monipuolinen rooli Zeta funktio. Sovelluksilla on erityisiä toiminnallisia arvoja:

• Arvo on mm. laskettaessa kriittistä lämpötilaa niin kutsutun Bose-Einstein-kondensaatin muodostamiseksi ja spin-aaltoteoriassa magneettisissa järjestelmissä.${\ displaystyle \ zeta (3/2) \ noin 2 {,} 61237}$

• Arvoa käytetään harmonisen oskillaattorin tilojen tiheyden korkeassa lämpötilarajassa .${\ displaystyle \ zeta (2) \ noin 1 {,} 64493}$

• Arvoa käytetään tilojen tiheydessä vapaalle bosonikaasulle .${\ displaystyle \ zeta (5/2) \ noin 1 {,} 34148}$

• Vakio liittyy kiinteä ja säteilyn tiheys on Planckin mustan kappaleen säteilyä .${\ displaystyle \ zeta (4) \ noin 1 {,} 08232}$

Lisäksi ns. Toistaa zeta-funktion säätelyn ( Zeta-funktion säännönmukaisuus ) roolin kvanttikenttäteorian erojen tasaamisessa . Ramanujanin tapaan hajautetuille sarjoille annetaan rajalliset arvot. Esimerkki tällaisesta laillistamisesta koskee Casimir -vaikutusta .

Ramanujanin ja Eulerin kaavaa voidaan käyttää heuristisesti johtamaan yksinkertaisella tavalla 26 avaruus-aikaulon välttämättömyys bosonian merkkijonoteoriassa .${\ displaystyle \ zeta (-1)}$

Zipfin laki

Zipfin laki on alun perin muotoiltu kvantitatiiviseen kielitieteeseen ja siinä todetaan, että luonnollisen kielen lausuntojen joukossa sanan taajuus on kääntäen verrannollinen sen asemaan taajuustaulukossa. Yleisin sana esiintyy siis noin kaksi kertaa niin usein kuin toiseksi yleisin sana, kolme kertaa niin usein kuin kolmanneksi yleisin sana jne. Eri sanoja käytettäessä tämän todennäköisyysjakauma on ${\ displaystyle N}$

${\ displaystyle P (X = n) = {\ frac {1} {nH_ {N}}}}$

kanssa harmoninen sekvenssi johdonmukaisuutta. Tietojoukon tyypistä riippuen saatetaan kuitenkin tarvita toinen eksponentti . Yleisellä harmonisella sekvenssillä voidaan saada yleinen jakauma todellisille parametreille${\ displaystyle H_ {N}}$${\ displaystyle \ texttyle H_ {N} ^ {(s)} = 1 + {\ frac {1} {2 ^ {s}}} + \ cdots + {\ frac {1} {N ^ {s}}} }$${\ displaystyle s}$

${\ displaystyle P (X = n) = {\ frac {1} {n ^ {s} H_ {N} ^ {(s)}}}}$

kuvata. Tässä tapauksessa tätä voidaan käyttää zeta -jakelun luomiseen, joka sopii "äärettömän monelle sanalle" :${\ displaystyle s> 1}$

${\ displaystyle P (X = n) = {\ frac {1} {n ^ {s} \ zeta (s)}}.}}$

Maailmanlaajuiset ominaisuudet

Toiminnallinen yhtälö

Toiminnon todellinen kaavio , peilisymmetria näkyy selvästi suoralla x = 1/2${\ displaystyle x \ mapsto \ zeta (x) \ Gamma (x / 2) \ pi ^ {- x / 2}}$

Seuraavassa tarkoittaa gammafunktion että yleistää kertoma monimutkaisia numeroita. Kaiken kaikkiaan pidetään meromorfisten funktioiden identiteettiä${\ displaystyle \ Gamma (\ cdot)}$${\ displaystyle \ mathbb {C}}$

${\ displaystyle \ zeta (1-s) = {\ frac {2} {(2 \ pi) ^ {s}}} \ \ cos {\ frac {\ pi s} {2}} \ \ Gamma (t) \ \ zeta (t).}$

Vaihtoehtoinen esitys syntyy tästä yksinkertaisella muutoksella

${\ displaystyle \ zeta (s) = 2 ^ {s} \ pi ^ {s-1} \ sin {\ frac {\ pi s} {2}} \ \ Gamma (1-s) \ \ zeta (1 -s)}$

kaikille . Myös funktionaalisen yhtälön symmetristä muunnosta käytetään usein , nimittäin ${\ displaystyle s \ in \ mathbb {C} \ setminus \ lbrace {0,1 \ rbrace}}$

${\ displaystyle \ Gamma \ vasen ({\ frac {s} {2}} \ oikea) \ \ pi ^ {- s / 2} \ \ zeta (s) = \ Gamma \ vasen ({\ frac {1-s } {2}} \ oikea) \ \ pi ^ {(s-1) / 2} \ \ zeta (1-s),}$

viitattu kirjallisuudessa. Huomaa muuttujanmuunnoksen alla syntyvä invarianssi . Yllä olevat yhtälöt voidaan johtaa symmetrisestä variantista käyttämällä Legendren monistuskaavaa ja Eulerin lisäteoriaa. ${\ displaystyle s \ mapsto 1-s}$

Edellä mainitun tyyppisen toiminnallisen yhtälön täyttyminen on ominaista L-funktioille (erityinen Dirichlet-sarja, muun muassa analyyttinen jatko). Muunnoskäyttäytymisensä vuoksi nämä liittyvät usein modulaarisiin muotoihin . Esimerkiksi zeta-funktio vastaa Jacobian teeta-funktiota , modulaarista puolipainon painoa. Tästä suhteesta aloitetaan teeta -funktion, funktionaalisen yhtälön, muutoskäyttäytymisellä .

Funktionaalinen yhtälö luo yhteyden tärkeiden matemaattisten funktioiden välille ja johtaa tärkeisiin tuloksiin zeta -funktion nollien ja kasvukäyttäytymisen suhteen . Seuraava periaate on yhteinen monille johtopäätöksille: Koska zeta-funktion yksinkertainen käyttäytyminen puolitasossa (Dirichlet-sarjan absoluuttisen lähentymisen vuoksi) , puolitason trivialisointi saavutetaan automaattisesti peilattu puolitaso . ${\ displaystyle \ operaattorinimi {Re} (s)> 1}$${\ displaystyle s \ mapsto 1-s}$${\ displaystyle \ operaattorinimi {Re} (t) <0}$

Kompleksikaavio funktion arvojen värillä : Riemann -funktio kompleksiluvutasossa${\ displaystyle \ xi}$

Työssään Riemannin perin määritelty koko toiminto${\ displaystyle s = 1/2 + \ mathrm {i} t}$

${\ displaystyle \ Xi (t) = {\ frac {1} {2}} s (s-1) \ \ pi ^ {- s / 2} \ \ Gamma \ vasen ({\ frac {s} {2} } \ oikea) \ \ zeta (t).}$

Nykypäivän sopimuksessa on kuitenkin tavallisempaa käyttää muuttujaa muuttujan sijaan ; sitten panostat . Tässä uudessa merkinnässä heijastus pätee ${\ displaystyle t}$${\ displaystyle s}$${\ displaystyle \ xi (1/2 + \ mathrm {i} t): = \ Xi (t)}$

${\ displaystyle \ xi (s) = \ xi (1-s).}$

Molempia tulkintoja kutsutaan nykyään Riemann Xi -funktioksi .

Toiminnallinen yhtälö oli jo Eulerin tiedossa (1749), vaikka hän ei muotoillut sitä monimutkaisiin väitteisiin eikä todistanut sitä, vaan tarkisti sen vain niin monessa tapauksessa, että hänen sanojensa mukaan ei ollut epäilystäkään sen pätevyydestä. Todisteita julkaisivat myös Oskar Schlömilch vuonna 1858 ja Carl Johan Malmstén (1849). André Weil huomautti, että todiste funktionaaliyhtälö kanssa Mellin muutos on jo kirjoitettu kädessä kopio Gaussin Disquisitiones Arithmeticae mukaan Gotthold Eisenstein , joiden kanssa Riemannin oli läheisiä ystäviä hänen aikanaan Berliinissä.

Hampurilaisen luonnehdinta

Vuonna 1921 Hans Hamburger onnistui luonnehtimaan Riemannin zeta -funktion toiminnallisen yhtälön avulla seuraavasti.

Anna , jossa koko funktio rajallinen järjestys ja on polynomifunktio , voidaan esittää , että dirichlet'n sarja . Toiminnallinen yhtälö pätee myös ${\ displaystyle f (s) = G (s) / P (s)}$${\ displaystyle G (s)}$${\ displaystyle P (s)}$${\ displaystyle \ operaattorinimi {Re} (s)> 1}$${\ displaystyle \ texttyle f (s) = \ summa a (n) / n ^ {s}}$

${\ displaystyle f (s) \ Gamma \ vasen ({\ frac {s} {2}} \ right) \ pi ^ {- {\ frac {s} {2}}} = g (1-s) \ Gamma \ vasen ({\ frac {1-s} {2}} \ oikea) \ pi ^ {-{\ frac {1-s} {2}}},}$

jolloin se voidaan esittää myös puolitasossa Dirichlet-sarjana . Sitten identiteetti seuraa jo .${\ displaystyle g (s)}$${\ displaystyle \ operaattorinimi {Re} (s)> 1}$${\ displaystyle \ texttyle g (s) = \ summa b (n) / n ^ {s}}$${\ displaystyle f (s) = g (s) = a (1) \ zeta (s)}$