Leonhard Eulerin tieteellinen työ
Tieteellinen työ Leonhard Euler on laajin koskaan luotu matemaatikko. Se sisältää perustulokset laskennan , analyysin , mekaniikan , tähtitieteen , geodeesin , lukuteorian , algebran , trigonometrian , geometrian , musiikkiteorian ja optiikan aloilla .
Eulerin tunnetuimpiin tuloksiin kuuluvat Baselin ongelman ratkaisu , polyhedronikorvaus ja Eulerin identiteetti , joista jälkimmäinen muodostaa läheisen yhteyden lukemattomien matemaattisten vakioiden välille . Näistä ja muista tuloksista Euler sai monia postuumia kunniamerkkejä.

Eulerin tutkimus oli hyvin monipuolista. Hän työskenteli melkein kaikilla matematiikan alueilla ja häntä pidetään yhtenä historian tuottavimmista matemaatikoista. Hänen toistaiseksi keräämät Opera omnia -teokset käsittävät 76 teosta. Hänen julkaisujaan on yhteensä 866. Eulerin nimeen liittyy suuri määrä tuloksia ja tieteellisiä aiheita.
Kaksi matemaattiset vakiot nimetty jälkeen Leonhard Euler : Eulerin luku välillä analyysi (ks eksponentiaalinen funktio ) ja Euler-Mascheroni vakio γ (gamma) määrä teoria, joka on joskus kutsutaan Eulerin vakio ja on noin yhtä kuin 0,57721. Ei tiedetä, onko y järkevä vai irrationaalinen . Sitä vastoin luvun e irrationaalisuus tunnetaan ja sen osoitti ensin Euler (katso myös: Todiste Eulerin luvun irrationaalisuudesta ).
Hänen suosittu tieteellinen tutkielmansa Lettres à une princesse d'Allemagne vuodelta 1768, jossa hän kirjoitti kirjeitä prinsessa Friederike Charlotte von Brandenburg-Schwedtille , Frederick II: n toisen asteen veljentytär , fysiikan perusteet, sai myös laajemman lukijakunnan. , filosofia ja teologia.
Leonhard Eulerin työllä oli pysyvä vaikutus moniin matemaatikkosukupolviin. Carl Friedrich Gauß sanoi : "Eulerin teosten opiskelu on edelleen matematiikan eri alojen paras koulu, eikä sitä voida korvata millään muulla". Koska julkaisuja ja kirjeenvaihtoa muiden matemaatikkojen ja henkilöiden kanssa on paljon, pyrkimyksiä julkaista täydellinen Eulersin työ jatkuu tähän päivään saakka. Kuitenkin julkistamisen Opera Omnia jonka Euler komission , tämä sitoumus katsotaan on toteutettu mahdollisimman laajasti.
Matemaattiset merkinnät
Euler esitteli useita merkintätapoja lukuisissa oppikirjoissaan. Kirjojen laajan käytön vuoksi monet hänen merkinnöistään vakiintuivat. Hän esitteli matemaattisen funktion käsitteen ja kirjoitti ensimmäisenä f (x) merkitsemään funktiota f , jota käytetään argumenttiin x . Eulerin käyttämä "muodollinen" termi oli tärkeä virstanpylväs kohti nykypäivän määritelmää:
"Jos muuttujat ovat toisistaan riippuvaisia siten, että kukaan niistä ei voi kokea muutosta aiheuttamatta samalla muutosta toisessa, niin sitä, jonka muutosta pidetään toisen muutoksen vaikutuksena, kutsutaan tämä termi ulottuu niin pitkälle, että se kattaa kaikki tapat, joilla toinen voi määrittää yhden määrän. "
Merkinnät varten trigonometriset funktiot , kirjain E varten pohjan luonnollinen logaritmi , kreikkalainen kirjain Σ ( sigma ) ja summien ja kirjain i varten nimeämiseen imaginääriyksikköä tulevat hänestä . eron symboli Δ ( delta ) on myös Euler. Euler myös suositteli kreikkalaisen π-kirjaimen käyttöä kehän ja halkaisijan ( ympyrän numero ) suhteen osoittamiseksi, vaikka se alun perin palasi Walesin matemaatikolle William Jonesille .
Analyysi ja toimintateoria
Perusanalyysi
Euler voidaan nähdä yhtenä analyysin perustajista . Matematiikan historioitsija Thomas Sonar kuvailee kirjassaan 3000 vuotta analyysia (2011) Leonhard Euleria "todellisena jättiläisenä analyysin tekemiseksi". Eulerin merkitystä tälle kentälle ei korosta pelkästään tiukka toiminnallinen käsite. Hän on "lyömätön mestari" käsitellessään tehosarjoja , jotka hän ymmärsi "äärettömäksi polynomiksi " ja teki pysyvän "työhevosensa".
Euler oli edelläkävijä analyyttisten menetelmien käytön ongelmien ratkaisemisessa lukuteoriassa. Tällöin hän yhdisti kaksi erilaista matematiikan osaa ja esitteli uuden tutkimusalueen, analyyttisen lukuteorian .
kalkki
Jatkuvan tutkimuksen takia kiven määrä oli nousussa 1700-luvulla. Erityisesti Eulerin ystävät, Bernoullit, olivat vastuussa suuresta osasta tämän alueen varhaisia edistysaskeleita. Vaikuttavuutensa ansiosta laskennan tutkimuksesta tuli Eulerin työn pääpaino. Teoksessa Institutiones calculi differentialis (1755) hän käsitteli järjestelmällisesti differentiaalilaskua . Euler valitsi äärettömän pienille määrille tulkinnan: ”Pienempi kuin mikä tahansa määriteltävä määrä”. Vuonna Institutiones calculi differentialis 1755, Euler määritellään:
”Ei ole epäilystäkään siitä, että mitä tahansa kokoa voidaan pienentää, kunnes se katoaa ja siitä ei tule mitään. Mutta äärettömän pieni koko ei ole muuta kuin katoava koko ja siksi se on todella 0. "
Siksi Euler pitää äärettömän pienillä määrillä laskemista "nollien laskemiseksi". Tätä varten hän esitteli "äärettömän pienen" koon ja "äärettömän suuren" koon (ei pidä sekoittaa kuvitteelliseen yksikköön) - ja käytti näitä johtaakseen oikeita lauseita. Esimerkiksi Euler käytti lähestymistapaa, joka oli " alun perin voimassa mihin tahansa numeroon "
sarjan ympärillä, joka on voimassa Eulerin numerolle
johtaa. Tämä kaava antaa erittäin nopeasti yhtenevän sarjan numerolle , esimerkiksi sillä on luku
Eulerin kaavan taustalla on mainittava, että raja-arvolle
Pätevä on se, mikä luokittelee sen merkinnän matemaattisen Limesin modernille kielelle .
Taylor-sarja
Euler tunnetaan tässä yhteydessä kehittämiseksi ja usein toistuva käyttö potenssisarjojen . Nämä voidaan ymmärtää "äärettömän pitkiksi polynomeiksi ", joista funktio voidaan "rekonstruoida globaalisti" joissakin tapauksissa sen paikallisen käyttäytymisen perusteella (ts. Tietämällä kaikki sen johdannaiset ja piste). Muun muassa hän antoi suorat todisteet Taylor-sarjoista eksponentiaalifunktiosta
ja arktangenttitoiminto . Epäsuorat todisteet tulevat Newtonilta ja Leibniziltä ajanjaksolta 1665-1680. Euler kehitti myös sini- ja kosinusfunktiot Taylor-sarjassaan kehityskohdan 0 ympärillä:
Hän käytti tätä johtaakseen Eulerin kaavan eksponenttifunktiolle yksinkertaisesti lisäämällä sen .
Äärettömät rivit
Vuonna 1736 hän löysi (myös käyttämällä tehosarjoja) kauan tavoitellun raja-arvon vastavuoroisten neliölukujen äärettömälle summalle :
Jos täsmää ”kaikki” (äärettömän monta) vastavuoroinen arvot neliön numerot, tulos on numero . Tämä tarkoittaa, että jokainen pieni määrä (noin ) neliön numero on olemassa sellainen, että kaikki seuraavat neliöt sovelletaan
Koska hän oli käyttänyt aiemmin tuntemattomia manipuloinnin tekniikoita potenssisarjoja tähän tulokseen , hänen alkuperäinen näyttöä oli ei hyväksytty. Euler julkaisi kuitenkin toisen todistuksen vuonna 1743. Tämän niin kutsutun Baselin ongelman yleistämisestä hän johti suljetun edustuksen parillisille Bernoulli-numeroille . Hän osoitti esimerkiksi, että kaikkien neljännen ja kuudennen voiman vastavuoroisten arvojen summa pyrkii myös vastaavien voimien järkiperäisiä kerrannaisia vastaan .
ja yleensä
Tätä on pitkään pidetty parhaana menetelmänä laskea Bernoullin luvut .
Hän käytti henkilöllisyyttä
kanssa arkustangentin on saada nopeasti suppenevan sarja . Äärettömät rivit kuten esimerkiksi
tai
kanssa Riemannin Zeta funktio myös palata Euler. Euler oli ensimmäinen, joka tutki järjestelmällisesti erilaisia sarjaa .
Trigonometriset toiminnot
Euler on ensimmäinen tekijä, joka koskee trigonometriset funktiot on ympyrän kanssa säde 1 ja siten normalisoi niitä. Tämä tapahtuu johdannon kuudennessa luvussa . Erityisesti seuraa heti Pythagoraan lause
Euleristä johdettiin järjestelmällisesti useita trigonometrian peruskaavoja. Hän käytti lisäksi teoreemojen trigonometriset funktiot ja oli ensimmäinen antaa yksinkertainen ja selkeä todiste De Moivre n tunnettuja kaava . Tämän päivän näkökulmasta tätä todistusta pidetään myös tiukana, jos jätetään huomiotta se tosiasia, että täydellistä induktiota ei ollut virallisesti saatettu päätökseen. Näistä kaavoista Euler sai trigonometristen funktioiden laajennuksen tehosarjoissa käyttämällä samaa menettelytapaa kuin eksponentiaalisen funktion tapauksessa.
Osamurtokehitelmä on cotangene käsiteltiin myös Eulerin tutkimuksen. Hän keskusteli tästä muun muassa 30. kesäkuuta 1742 päivätyssä kirjeessä Christian Goldbachille.
Monimutkaisen muuttujan toimintoja koskevien tutkimustensa yhteydessä , joista osa oli d'Alembertin ennakoimia, Euler pääsi tulokseen Johann Bernoullin jo käyttämän ei-todellisen korvaamisen avulla.
Tässä yhteydessä on syytä mainita, että Euler löysi tuotekaavan soveltamalla lisäyslausetta funktioihin useita kertoja
luotu.
Eksponentiaalinen funktio ja logaritmi

Euler käytti ensin eksponentiaalifunktiota ja logaritmeja analyyttisissä todisteissa ja määritteli ne onnistuneesti kompleksilukuille . Tämä laajensi huomattavasti niiden soveltamisalaa. Näin hän löysi läheisen suhteen trigonometrisiin toimintoihin. Jokaiselle reaaliluvulle ( radiaaneina ) Eulerin kaava sanoo , että kompleksinen eksponenttifunktio on yhtälö
Täyttää. Yllä olevan kaavan erityistapausta kutsutaan Eulerin identiteetiksi
kuuluisa. Eulerin kaava johtaa todisteisiin lisäyslausekkeista ja De Moivren kaavasta . Joten toisaalta
Eksponenttifunktion kerrottavuutta käytetään myös additiolauseissa. Toisaalta meillä on vastaavasti
Kaksi kompleksilukua ovat yhtä suuret ja vain, jos todellinen ja kuvitteellinen osa vastaavat toisiaan - esimerkiksi seuraava pätee .
Vaihtelulaskelman perustelut
Lagrangen ohella Euler on yksi variaatioiden laskijoiden perustajista . Jakobin ja Johann Bernullin useiden ongelmien ja ideoiden seurauksena Euler muotoili pääongelmansa hyvin varhaisessa vaiheessa ja kehitti yleisiä menetelmiä niiden ratkaisemiseksi. Tämä tapahtui hänen Methodus inveniendi lineas -kaaressa, joka julkaistiin vuonna 1744 . Tämän erityisen kurinalaisuuden (jonka Bernoulli-veljet aloittivat jossain määrin) suunnitteli ja järjesti ensin Euler. Se käsittelee ääriarvon ongelmia eniten yleistä tyyppiä . Päinvastoin kuin differentiaalilaskennassa , jossa usein määritetään funktioiden paikalliset maksimit tai minimit, variaatiolaskennalle on tunnusomaista ongelmat, joissa yksi tai useampi tuntematon funktio on määritettävä siten, että tietty integraali, joka on riippuvainen näistä funktioista olettaa äärimmäiset arvot.
Erierilaskennassa käytetty Euler-Lagrange-yhtälö on nimetty Eulerin mukaan .
Seuraava arvio on peräisin Carl Gustav Jacobilta:
”Tärkeintä Methodus inveniendissä on pieni liite, jossa osoitetaan, kuinka kehon kuvaama käyrä antaa minimin tietyissä mekaanisissa ongelmissa; oletetaan kuitenkin vain runko, joka liikkuu yhdessä tasossa. Koko analyyttinen mekaniikka on syntynyt pelkästään tästä liitteestä. Koska pian ulkonäönsä jälkeen Lagrange, Archimedesin jälkeen, kenties suurin matemaattinen nero, 20-vuotias, keksi analyyttisen mekaniikkansa ... Yleistämällä Eulerin menetelmän hän keksi outon kaavansa, jossa yhdellä rivillä kaikkien ratkaisu analyyttisen mekaniikan ongelmat sisältyvät ".
Integraalilaskenta
Kolmessa osassa julkaistussa teoksessa Institutiones calculi integralis (1768–1770) Euler käsitteli integraalilaskentaa . Määrittelemättömän integraation menetelmät löytyvät tyhjentävästi nykyaikaisessa muodossa niissä tapauksissa, joissa integraatio johtaa alkeistoimintoihin. Euler kehitti ensin monia menetelmiä, ja Eulerin korvaaminen , jonka avulla tietyt irrationaaliset erot voidaan järkeistää, on edelleen käsite. Hän löysi tavan laskea integraalit monimutkaisilla rajoilla ennakoiden siten monimutkaisen analyysin tärkeitä osia .
On huomattava, että Laplace Laplace -nimestä nimetty esiaste muuttaa Eulerin jo jo 1766 Institutiones calculi integralis -sarjassaan . Laplace oli ensin käyttänyt sitä todennäköisyysteorian yhteydessä .
Fourier-sarja
Euler työskenteli myös Fourier-sarjassa . Hän ohjasi arvoille kelvollisen kaavan
linjan ulkopuolella
kohdassa :
Vaikka oikealla olevat sarjat eivät yhtene mihinkään, integroituminen molemmille puolille, oikean integraatiovakion valitsemisen jälkeen, antoi Eulerin sarjan, joka tunnetaan nykyään oikeena .
Tämä on tyypillinen esimerkki "algebran yleisyydestä", johon Euler perustuu. Vaikka joitain Eulerin todisteita ei voida hyväksyä nykyaikaisissa matemaattisen tarkkuuden standardeissa, hänen ideansa, kuten juuri osoitettiin, johtivat paljon edistystä.
Transsendenttitoiminnot
Tämän uuden alan edelläkävijänä Euler loi teorian hypergeometrisistä sarjoista , q-sarjoista ja hyperbolisista trigonometrisista funktioista .
Riemannin zeta-toiminto
Myös toiminnallinen yhtälö Riemannin Zeta funktio , Euler aiheeseen liittyvän toiminnon
muodossa
totesi, samoin kuin jotkut niiden arvoista negatiivisissa paikoissa, olivat jo Eulerin tiedossa. Tämä ei ole klassinen yhtälö , kuten vain arvo , mutta identiteetti eli yhtälö . H. yhtälö on oikea riippumatta siitä, mitä käytetään. Esimerkiksi, on (triviaali) identiteetti, ja zeta-funktion tapauksessa Euler loi yhteyden arvojen välille ja se pätee kaikille . Hän epäili tätä laajojen numeeristen laskelmien jälkeen, jotka perustuvat nykyään oikeaan esitykseen
perustuivat. Riemannin zeta-funktiolla on erittäin tärkeä rooli lukuteoriassa, ja funktionaalista yhtälöä käytti Bernhard Riemann , joka esitti tiukan todistuksen ensimmäistä kertaa, rakentaakseen teoriansa alkulukuihin .
Beeta- ja gammafunktio
Jo vuonna 1729 Euler kehitti luonnollisille numeroille kelvollisen kaavan binomilauseen avulla
Tästä hän johti kiinteän esityksen tiedekunnan toiminnalle :
Nämä tulokset johtivat siihen, että Euler löysi beeta- ja gammafunktiot ja tutki niiden perusominaisuuksia. Kirjeessä Christian Goldbachin kanssa vuonna 1729 Euler yleisti ensin tiedekunnan ja vuonna 1730 esitteli toisen tyypin Euler-integraalin, joka edustaa Euler-gammafunktiota monimutkaisille arvoille, joilla on positiivinen todellinen osa :
Jo kirjeen 1729 Christian Goldbach Euler oli kaava puoliluku tiedekunnan lomakkeessa mainitut: . Ensimmäisen luokan integraali edustaa beeta-funktiota :
Näiden toimintojen erityisominaisuuksista Euler paitsi johdatti suhteita Euler-Mascheroni-vakioon , mutta antoi myös tuotekaavat
ja
jälkimmäinen Eulerin lisäsarjana (Eulerin heijastuskaava) tunnetaan. Beeta-toiminto on perusteella beeta jakelu päässä todennäköisyysteoriaan . Gammafunktion näkyy gammajakauman , mutta myös soittaa tärkeä rooli vuonna funktio ja lukuteoria, muun muassa osana valmistunut L-toimintoja .
Elliptiset integraalit
Eulerin suuri kiinnostus elliptisiin integraaleihin ja elliptisiin toimintoihin kohdistuu jo varhaisiin vuosiin Johann Bernoullin kanssa . Opiskellessaan Berliinin Academy, Euler sai kahden volyymi työtä Giulio Fagnano 23. joulukuuta 1751 oikeus Produzioni Matematiche , joka julkaistiin vuonna 1750 hänen virallista tarkistusta. Tämä työ sisälsi kaavan kaksinkertaistaa kaaren pituuden lemniskaatista , jonka napakoordinaattiyhtälö ja algebrallinen yhtälö on. Euler innostui valtavasti tästä työstä ja auttoi luomaan uuden alueen algebrallisista toiminnoista .
Euler pystyi osoittamaan tuloksen, joka tunnetaan tänään elliptisten integraalien lisäyslauseena (ensimmäinen laji). Jos asetetaan kokonaisluvuilla , se seuraa tasa-arvosta
jo
Tätä kutsutaan Eulerin lisäyslausekkeeksi . Vuonna 1753 Euler löysi monia summauskaavoja elliptisille integraaleille, jotka yleensä liittyvät suoraan additiolauseeseen.
Numeroteoria ja kombinatorika
Eulerin kiinnostus lukuteoriaan voidaan jäljittää Christian Goldbachin , hänen ystävänsä Pietarin akatemiassa, vaikutuksiin. Numeroteoria on pohjimmiltaan luonnontieteiden ja niiden ominaisuuksien tiede . Määrä teoreettinen ominaisuus numero on, esimerkiksi, onko se voidaan jakaa toinen numero tai kuinka monta numeroa se voidaan jakaa. Esimerkiksi Euler sai oivalluksen siitä, että pariton luku on suurempi kuin vain jaollinen itsestään (on alkuluku ), jos on vain yksi mahdollisuus kirjoittaa sekvenssin lisäksi kahden suhteellisen alkupositiivisen neliön summa. Siksi sitä voidaan esittää luonnollisena lukuna samanaikaisesti . (Sama pätee analogisesti esimerkiksi alkulukujen neliöihin ). Esimerkiksi numerolla on ei-triviaalijakaja, joten se ei ole alkuluku
Mutta jos se pitää , että numerot ja ovat prime ja muuten ei ole enää mahdollisuutta hajoamisen kahteen epätriviaali neliöt. Joten on alkuluku. On kuitenkin huomattava, että toisaalta kaikkia alkulukuja ei voida kirjoittaa kahden neliön summana. Vain lomakkeen alkuluvut ovat aina kahden neliön luvun summa. Suuri osa Eulerin aikai- sesta numeroteorian työstä perustuu Pierre de Fermatin teoksiin . Euler kehitti joitain Fermatin ideoita ja kumosi jotkut hänen arvauksistaan.
Erilaiset numerot ja numerosarjat on nimetty Eulerin mukaan , katso Eulerin numerot (erittely) .
Perusnumeroteoria
Esimerkiksi hän kumosi Fermatin olettamuksen, jonka mukaan kaikki Fermat-luvut ovat myös alkulukuja osoittamalla, että luku on jaettavissa 641: llä.
Hän vaikutti merkittävästi täydellisten lukujen teoriaan , joka oli kiehtonut matemaatikkoja Euclidesta lähtien . Euler osoitti, että suhde (parillisten) täydellisten numeroiden ja Euclidin osoittamien Mersennen alkulukujen välillä on jopa yksi yhteen , tulos tunnetaan nimellä Euclid-Euler-lause . Vuonna 1772 Euler totesi Goldbachille lähettämässään kirjeessä oikein, että 2 147 483 647 on Mersennen alkuluku. Sitä pidettiin suurimpana päälukuna vuoteen 1867 asti. Jo 1732 hän pystyi saamaan täydellisen 19-numeroisen numeron
rakentaa.
Algebrallinen lukuteoria
Hän antoi useita todisteita Fermatin pienestä lauseesta ja julkaisi ensimmäisenä todistuksen (Leibnizin vuonna 1683 antama todiste ilmestyi vasta vuonna 1894). Hänen ensimmäinen todiste oli induktio , mikä oli epätavallista tuolloin. Hän esitteli myös Eulerin phi-toiminnon . Käyttämällä tämän toiminnon ominaisuuksia hän yleisti Fermatin pienen lauseen niin kutsuttuun Eulerin lauseeseen.
Euler teki tärkeän valmistelutyön Lagrangen neljän neliön lauseelle osoittamalla vuonna 1751, että jokainen positiivinen rationaaliluku voidaan kirjoittaa neljän rationaalisen neliön summana. Jo aiemmin, vuonna 1748, hänellä oli henkilöllisyys kirjeessä Goldbachille
mainitun, mikä vähensi ongelman alkulukuihin. Kun Lagrange osoitti, että mikä tahansa positiivinen kokonaisluku voidaan kirjoittaa neljän kokonaisen neliön summana, Euler toimitti yksinkertaisemman todistuksen pian sen jälkeen. Se pätee esimerkiksi
Toinen ajatus Eulerin työstä, joka syntyi hänen huolestuneisuudestaan Partitio numerorumin kanssa , on todistaa Lagrangen lause. Tätä varten hän katsoi tehosarjaa
jossa neljän neliösumman lause kaikille n on riittävä. Euler vihjasi tähän todisteideaan kirjeillä Goldbachille ja joissakin paperissa (kuten E394, E586). Joten hän kirjoitti elokuussa 1750: "Tämä tapa on mielestäni luonnollisin tapa päästä todisteeseen [...]". Tarkasteltu tehosarja on modifioidun teetasarjan neljäs voima - Jacobi myöhemmin kävi tällä tavalla todistamaan Lagrangen lauseen puhtaasti analyyttisesti.
Hän näytti myös Fermatin lauseen kahden neliön summasta . Tämä tarjoaa kriteerin sille, milloin positiivinen kokonaisluku voidaan kirjoittaa kahden kokonaisen neliön summana. Esimerkiksi seuraava koskee , mutta numerolle ei ole mahdollista tällaista hajoamista.
Euler näytti Fermatin suuren lauseen tapauksista ja . Hän osoitti, ettei yhtään nollaa suurempaa neliölukua voida kirjoittaa kahden yli nollan suuruisen neliön summana, mikä tarkoittaa jo sitä, että yhtälöllä ei ole positiivisia kokonaislukuratkaisuja. Siinä tapauksessa, Euler laskelmiin on . Käyttämällä tätä Gaussin numeroiden muunnosta ja implisiittistä oletusta ainutlaatuisesta tekijöistä Euler pystyi rakentamaan todistuksen, joka osoitti tapauksen mahdottomuuden . Kuten tapaustodistuksessaan , Eulerin todisteet perustuivat ensisijaisesti algebrallisten symbolien ja pariteettiargumenttien manipulointiin ja esittivät vähän uutta menetelmää. Kuten hänen jälkeensä matemaatikkosukupolvet, Euler epäonnistui Fermatin suuren lauseen yleisessä todistuksessa. Andrew Wiles ja Richard Taylor antoivat täydellisen todistuksen vasta vuonna 1995 osittain stabiilien elliptisten käyrien modulaarisuuslauseen seurauksena .
Euler epäili toisen asteen vastavuoroisuuden lakia , jonka myöhemmin todisti Carl Friedrich Gauß . Tämä on yksi lukuteorian peruskäsitteistä.
Kombinaattorit
Vaikka kombinatorikoista tuli vasta myöhemmin uusi moderni matematiikan haara, laskemisongelmilla on pitkä ja varhainen historia. Euler käsitteli permutaatioiden ja yhdistelmien ongelmia ja muotoili erityisen ongelman seuraavasti: Kuinka monta mahdollisuutta kirjainten järjestyksessä on järjestellä niin, että yksikään niistä ei palaa alkuperäiseen asentoonsa? Tässä yhteydessä Euler esitteli merkinnän edustamaan niiden kirjaimien permutaatioiden määrää , joissa yksikään kirjaimista ei palauta alkuperäistä asemaansa. Tällainen permutaatio tunnetaan nykyään kiinteän pisteen vapaana permutaationa .
Yksinkertainen argumentti, Euler osoittautui useita rekursiokaavojen varten , mukaan lukien kaksinkertainen rekursiokaava
Hän antoi myös nimenomaisen kaavan
mikä osoittaa, että kiinteiden pisteettömien permutaatioiden ja kaikkien permutaatioiden osamäärä lähenee nopeasti lukumäärää .
Viisikulmainen lukulause perustuu myös Euleriin
takaisin, hän osoitti sen 1750. rekursiokaavan varten väliseinät voidaan johdetut. Tätä käytti Percy Alexander MacMahon laskemaan osiofunktion arvot ylöspäin . Laskeva funktio on se, kuinka monta tapaa voidaan kirjoittaa luonnollisten lukujen summana. Esimerkiksi johtuu siitä . Se pätee . Viisikulmainen lukulause on myös kulmakivi combinatoricsin ja modulaaristen muotojen teorian välillä .
Analyyttinen lukuteoria
Euler yhdisti alkulukujakauman luonteen analyysin ideoihin. Hän esimerkiksi osoitti, että alkulukujen vastavuoroisten arvojen summa eroaa . Tällöin hän löysi yhteyden Riemannin zeta-funktion ja alkulukujen välillä; hänen löytönsä tunnetaan tänään nimellä Riemann zeta -funktion Euler-tuotekaava :
missä tuote ulottuu kaikkiin alkulukuihin . Kuten myöhemmin kävi ilmi, tällä henkilöllisyydellä on kauaskantoiset seuraukset lausekkeille alkulukujen jakautumisesta. Eulerin työ tällä alueella johti alkuluku-lauseen kehittämiseen .
Jatkuvat jakeet
Aikaisempien edeltäjiensä työn pohjalta Euler aloitti tutkimuksen jatkuvista murto- osista ja julkaisi vuonna 1737 teoksessa nimeltä De Fractionibus Continuis monia uusia ideoita ja tuloksia. Hän osoitti myös, että mikä tahansa rationaaliluku voidaan edustaa äärellisellä jatkuvalla murtoluvulla, ja löysi lukemattomalle jatkuvalle murtoluvulle seuraavan muodon:
Tästä (ja yhtä ääretön esitys kuin ketjumurtoluku varten ) Euler päätelty irrationaalisuuden ja . Hän antoi epäsäännölliset jatkuvat murtoluvut (ilman vain uusien murtolukujen osoittajia) ympyränumerolle , kuten
Hän osoitti myös lauseen, joka sanoo, että neliöllisen yhtälön ratkaisu on todellinen vain ja vain, jos sillä on jaksoittainen jatkuva murtolaajennus.
Euler-Mascheronin vakio
Euler löysi ensimmäisen kerran vuonna 1734 (mahdollisesti aikaisemmin) yhteyden luonnollisten logaritmien kasvun ja harmonisen jakson välillä . Vaikka termit pyrkivät kohti arvoa 0 kasvamaan arvoja , seuraava pätee
Joten kaikkien luonnollisten lukujen vastavuoroisten arvojen summa on rajaton. Jos kuitenkin vähennetään termi harmonisesta sekvenssistä , rajoittamaton kasvu poistetaan ja ero lähenee arvoon, jota nyt kutsutaan Euler-Mascheronin vakiona tai Eulerin vakiona :
Tästä perusmäärittelystä huolimatta algebralliset ominaisuudet tähän päivään asti ovat suurelta osin selittämättömiä. Sen uskotaan olevan irrationaalinen , mutta tästä ei ole vielä löydetty todisteita. Vuonna 1736 hän oli jo laskenut paperin E47 numeron 15 numeroksi .
Geometria, topologia ja graafiteoria
geometria
Euler teki suurimman osan löytöistään geometriassa käyttämällä algebrallisia ja analyyttisiä menetelmiä. Opetusrakenne, sekä tasainen että pallomainen trigonometria, on nykyisen muodon - mukaan lukien merkinnän - velkaa Leonhard Eulerille. Hänen Johann Bernoullin aloittamat tutkimukset pinnan geodeettisista viivoista olivat suuntausta määritteleviä myöhempää differentiaaligeometriaa varten . Vielä tärkeämpää oli hänen löytöjä alueteoriassa , josta Gaspard Monge ja muut tutkijat jatkoivat myöhemmin. Myöhempinä vuosina Euler jatkoi lopulta avaruuskäyrien yleisen teorian parissa työskentelyään tarkalleen siellä, missä Clairaut oli lopettanut vuonna 1731 - vaikka ne painettiin vasta postuumisti.
Differentiaaligeometrian perusteissa hän osallistui käyrän kaarevuuteen ja johti analyyttisen kaavan värähtelevien ympyröiden säteille . Hän löysi myös kaksi pinnan normaalia pääosaa ja pääkaarevuudet ja . Yksi hänen tuloksistaan, ns. Eulerin yhtälö, antaa minkä tahansa muun normaalin osan kaarevuuden , joka muodostaa kulman yhden pääkaarevuuden kanssa olevan osan kanssa, muodossa Euler käsitteli ensin kehitettäviä pintoja (esim. Sylinteri) tai kartio ) käytetty, d. H. Pinnat, jotka voidaan muodostaa muodoksi tasoksi ilman vääristymiä, kuten venyttämistä tai repeämistä. Pintaa kutsutaan hallituksi pinnaksi (esim. Sylinteri, kartio, hyperboloidi tai hyperbolinen paraboloidi ), jos se voidaan luoda siirtämällä suoraa viivaa avaruudessa.
Tiedetään, että Euler määritteli puhtaasti matemaattisesti ympyrän kierteen, jonka ensin tutkivat Jakob Bernoulli ja Christiaan Huygens , suotuisimpana profiilimuotona vaihteiden sivuille. Järkevästi käytettynä tämä käyrä tarjoaa optimaaliset mekaaniset ominaisuudet kitkahäviön, alhaisen melutason ja voimansiirron suhteen (tämä Eulerin löytö tai keksintö toteutettiin teknisesti vasta 1800-luvulla vastakkaisella hammastuksella ). Vähemmän tunnettua on, että tässä teoksessa E330, joka kirjoitettiin jo vuonna 1762, Euler ennakoi yhtälöä, joka on nyt nimetty Felix Savaryn mukaan . Sitä käytetään määrittämään säde on kaarevuuden liikkuvan käyrä ja mahdollistaa sen kaarevuuskeskukset on rakennettava elegantisti.
Sisällä alkeis geometria, Euler käsittelee muun muassa, jossa on edelläkävijä kaksinkertainen suhteen ja "pikku kuu" on Hippokrates . Hän omisti kaksi laajasti sijoitettua teosta E73 ja E423 jälkimmäiselle. Lyhyessä tutkielmassa E648 vuodelta 1779 Euler ratkaisi Apolloniuksen niin sanotun taktisen ongelman . Tämä edellyttää (alkeisvaiheessa aina mahdollista) (neljännen) ympyrän rakentamista, joka koskettaa kolmea mielivaltaisesti annettuja ympyröitä tasossa. François Viète , Isaac Newton ja muut ratkaisivat tämän ongelman kuitenkin jo ennen Euleria . Pian sen jälkeen julkaisussa E733 hän yleisti ongelman kolmiulotteiseen tilaan ja löysi kosketuspallon rakenteen neljänä mielivaltaisesti annettuina pallona. Myös tämä rakenne johtaa vain asteen yhtälöön ja voidaan sen vuoksi suorittaa alkeellisella tavalla.
topologia
Euler ilmoitti Berliinistä Christian Goldbachille Pietarissa 14. marraskuuta 1750 päivätyllä kirjeellä löytäneensä perussuhteen kuperan monikulmion tärkeiden kokojen välillä. Hänen löytö oli kaava kuperan monikulmion , tasomaisen graafin , pisteiden ( E ), reunojen ( K ) ja pintojen ( F ) lukumäärälle. Nykyään tätä teosta kutsutaan Eulerin polyhedron- lauseeksi.
Todennäköisesti kaikkein näkyvin kupera polyhedron on kuutio : Siinä on 8 kulmaa, 12 reunaa ja 6 pintaa,
8-12 + 6 = 2Dodekaedri on 20 vertices, 30 reunoja ja 12 kasvot. Seuraava pätee:
20-30 + 12 = 2Ikosaedri on 12 vertices, 30 reunoja ja 20 kasvoja. Samanlainen kuin vasemmalla, 12-30 + 20 = 2 pätee
Kahdeksan vuotta kirjeensä jälkeen, vuonna 1758, hän julkaisi kaksi asiaa koskevaa paperia. Ensimmäinen sisälsi löytönsä, toinen yritys todistaa se. Eulerin todiste, jossa hän halusi hajottaa tutkitut kohteet yksittäisiksi tetraedreiksi , sisälsi vakavuusvirheen nykypäivän standardien mukaan. Henri Lebesgue korosti tätä aukkoa vuonna 1924 .
Euler toivoi pystyvänsä luokittelemaan kaikki polyhedrat työhönsä, mutta ei saavuttanut tätä tavoitetta. Näiden kahden teoksen julkaisemisen jälkeen hän ei enää kääntynyt aiheeseen.
Eulerin polyhedronjoukon vakio tunnetaan nyt kuvaajan (tai muun matemaattisen objektin) Euler-ominaisuutena ja se liittyy suoraan kohteen matemaattiseen sukupuoleen . Ensimmäinen täydellinen todiste polyhedronin korvaamisesta tuli vain Adrien-Marie Legendreltä . Tämän kaavan tutkiminen ja yleistäminen, erityisesti Cauchyn ja L'Huilierin toimesta , merkitsee ( algebrallisen ) topologian alkua .
Kuvaajateoria
Vuonna 1735 (julkaistiin vuonna 1741 teoksella Solutio problematis ad geometriam situs pertinentis ) Euler esitteli ratkaisun Königsbergin sillan ongelmaan . Kaupungin Königsbergin vuonna Preussin makasi Pregel joen ja käsitti kaksi suurta saarta, jotka olivat yhteydessä toisiinsa ja mantereeseen Seitsemän sillan. Ongelmana on päättää, onko mahdollista valita polku, joka ylittää jokaisen sillan täsmälleen kerran ja palaa lähtöpisteeseen. Tämä ei ole mahdollista, koska pariton määrä siltoja johtaa ainakin yhteen maaperään. Tämän ehdon täyttävät jo keskisaarelle johtavat sillat. Silta Ongelmana on synonyymi kysymys onko Euler ympyrä , että kuvaajan vastaa kaupungin kartta .
Tätä ratkaisua pidetään graafiteorian , erityisesti tasomaisen teoriateorian , ensimmäisenä lauseena .
Soveltava matematiikka
Numerot ja differentiaaliyhtälöt
Euler-Maclaurin-kaava
Euler löysi kaavan vuonna 1732
kanssa Bernoulli numerot ja loput
Bernoulli tarkoittaa polynomia . Tämän löysi itsenäisesti Colin Maclaurin ja sitä kutsutaan nyt Euler-Maclaurin-kaavaksi . Kaava luo summan ja integraalin välisen suhteen . Takana olevat termit sisältävät rajapisteiden (korkeammat) johdannaiset, ja ne voidaan yleensä laskea nopeasti fiksulla (yleensä ei liian korkealla) valinnalla . Eulerin ja Maclaurinin empiirinen kaava on hyödyllinen, kun summa on hyvin vaikea laskea, mutta integraali on helppo laskea. Esimerkiksi on
vaikea laskea laskun aikana
on paljon helpompi suorittaa (katso myös: Integral calculus and antiderivative ) - on huomattava, että summa-kaavaa ei ole asetettu mihinkään tiettyyn rajaan, ja se voi siksi alkaa myös yhdellä 0: n sijaan. Vaihtoehtoisesti, jos aloitat suuresta lähtöarvosta , niin se on noin
Toisaalta empiiristä kaavaa voidaan käyttää arvioimaan integraali (jota on vaikea laskea) käyttämällä erillisiä summia. Vastaavasti Euler käytti tätä kaavaa hyödyntämällä nopeasti numeerisesti likimääräisiä loputtomia sarjoja, jotka lähestyvät hitaasti. Joten hän antoi hyviä arvioita arvojen ja ja löysi täsmälleen 20 numeroa:
Jos Euler olisi sen sijaan "naiivisti" koonnut ehdot tällaisen tarkkuuden saavuttamiseksi , vaadittu aika 20 sekunnilla per kesä olisi ollut noin 63 biljoonaa vuotta. On osoitettu, että Eulerin alkuperäinen menetelmä suurempien arvojen laskemiseksi vahvisti numeerisen matematiikan uudeksi tutkimusalueeksi.
Selkeä Euler-menetelmä
Seitsemästoista ja kahdeksastoista vuosisadan aikana matemaatikot yrittivät vakavasti yrittää ratkaista tavanomaisia differentiaaliyhtälöitä perustoimintojen ja kvadratuurien suhteen. Kun nämä menetelmät epäonnistuivat, he ratkaisivat yhtälöt käyttämällä loputtomia sarjoja ja numeerisia menetelmiä. Vuonna 1768 Euler kehitti yksinkertaisen rajallisen erotusmenetelmän tavallisen differentiaaliyhtälön numeeriselle ratkaisulle
annetulla alkutilalla . Yhdenmukaista askelkoon pisteiden välillä , Euler rakennettu pistettä kanssa , ja sai sitten kaava
Tarkoitetaan tässä O merkintätapa Landau ja tässä tapauksessa tarkoittaa, että virhe melu ylittää oikean ilmaisun lähinnä "pieni" määrä ei ylity. Jos on jatkuva, niin sekvenssin Euler monikulmion linjat suppenee tasaisesti kanssa on tuntematon toiminto on riittävän pieni suljetulla välillä, joka sisältää.
Eulerin kulma
Tärkeät Eulerin kulmat on nimetty hänen mukaansa. Se on kolminkertainen kulmat , joiden orientaatio (kiertoasennon) kiinteän kappaleen kolmiulotteisessa euklidinen avaruus voidaan kuvata. Algebrallisen kuvauksen, jonka avulla minkä tahansa pisteen pyörimisasento voitiin laskea, Euler muotoili vain syvemmässä kasvussa vuodesta 1775 eteenpäin. , Ensimmäisessä hän osoitti, että yhdeksän elementit kartoitus matriisin (jotka kuvaavat kierto) ovat ole riippumattomia toisistaan , koska pituus tarkkuutta liikkeen, mutta määritetään vain kolme toisistaan riippumatonta kulmat, Euler kulma.
Vuonna aerodynamiikka on lentokoneen , Euler kulmat ovat tottuneet tähän päivään. On yleistä käytäntöä käyttää maan kiinteää koordinaatistoa kuvaamaan lentokoneen sijainti ja suunta suhteessa maahan. Koska koordinaatisto ole karteesinen järjestelmä , on yleensä joitakin ongelmia muotoiluun lentokoneen dynamiikkaa. Tätä voidaan torjua edelleen eriyttämällä. Kun taas ilma-aluksen paikan voidaan parhaiten kuvata avulla maa-kiinteä koordinaatistossa, komponentit inertia tensor yhtälön liikkeen kuvataan parhaiten avulla koordinaatistossa, joka on keskustan ja painopisteen ilma-alukseen sen alkuperä. Lentokoneen suuntaus maahan nähden voidaan nyt kuvata käyttämällä ns. Eulerin kulmia. Siksi on välttämätöntä johtaa transformaatio kahden ylemmän koordinaatistojärjestelmän välillä kolmen Eulerin kulmakierroksen avulla.
Arpajaiset
Euler käsitteli myös arpajaisia . Vuonna 1749 italialainen liikemies nimeltä Roccolini kääntyi Frederick Suuren, silloisen Preussin kuninkaan, puoleen ehdotuksella ottaa käyttöön arpajaisjärjestelmä, jossa tulisi piirtää viisi numeroa 1-90. Kuningas lähetti ehdotuksen tieteelliselle neuvonantajalleen Eulerille ja pyysi matemaattista tarkastusta valtion arpajaisten käyttöönotosta Saksassa. Kuninkaallisen pyynnöstä Euler kiinnostui hyvin genoilaisten arpajaisten järjestelmän eri näkökohtien analysoinnista ja kehitti parannetun arpajaisten järjestelmän käsiteltyään yhdistelmäkysymyksiä analysoitaessa tätä onnenpeliä. Tämän seurauksena Berliinin arpajaiset perustettiin Saksassa vuonna 1763.
Samana vuonna, kun Preussi järjesti ensimmäisen arpajaisensa , Euler luki paperin, jossa oli yksityiskohtainen ja yleinen analyysi tästä arpajaisesta Berliinin akatemian edessä. Eulerin teos julkaistiin postuumisti. Yksi perustavanlaatuinen tulokset Euler saavutetaan oli löytää kaava todennäköisyys voittaa vedon, jossa r on oikein arvata päässä t numerot vedetään ulos kokonaismäärään n . Hänen kaava oli:
Näitä todennäköisyyslaskelmia käyttämällä Euler laski kolme käytännön skenaariota kaikkien vetojen voitoille ottaen huomioon mahdollisuuden tuottaa voittoa arpajaisten järjestäjille.
väestönkasvu
Vuonna 1907, lähes 125 vuosi jälkeen Eulerin kuoleman, Alfred J. Lotka käyttää Eulerin työ Recherches Générales sur la kuolleisuusluku et la kertolasku du genre humain on saada Euler-Lotka yhtälön laskemiseksi väestön kasvu hinnat. Tämä on perustavanlaatuinen menetelmä, jota käytetään populaatiobiologiassa ja ekologiassa tähän päivään saakka.
fysiikka
mekaniikka
"Ohjelmansa" mukaan Eulerin mekaniikan tutkielmat voidaan jakaa seuraaville alueille: Mekaniikan perusteet (aineen rakenne ja rakenne, voima ja voimamitta, mekaniikan periaatteet), materiaalipisteiden mekaniikka, jäykän mekaniikka, mekaniikka joustava ei-elastinen, mekaniikka elastinen, nestemekaniikka ja kaasumaisten kappaleiden mekaniikka . Kirjoituksissa, kuten Mechanica, sive motus scientia analytica exposita (1736), Découverte d'un nouveau principe de mécanique (1752) ja Theoria motus corporum solidorum seu rigidorum (1765), Euler sovelsi matematiikkaa fysiikan kysymyksiin. Mukaan Clifford Truesdell, ”itse asiassa vähän liikettä, lisäävät paljon mekaniikkaa” toiseksi mainitut työt.
Jäykkä runkomekaniikka
Euler huomasi, että silloin yleisesti hyväksytyt mekaniikan periaatteet eivät olleet riittäviä ratkaisemaan jäykän rungon liikkeen ongelmaa kokonaisuudessaan. Lause, liikemäärämomentin (akselin ympäri kiinteän avaruudessa) löytyy jo - implisiittisesti muotoiltu - in Eulerin 1734 käsikirjoitus hänen Mechanica ja hänen Scientia navalis , joka kirjoitettiin vuonna 1738, mutta julkaistiin vasta 1749 . Erillisten massapisteiden järjestelmien kulmamomentin lause (suhteessa avaruuteen kiinnitettyyn akseliin) johdettiin ensimmäistä kertaa Eulerin tutkielmassa kuun solmujen liikkeestä, jonka Euler esitteli Berliinin tiedeakatemialle vuonna 1744 ja julkaistu vuonna 1750. 3. syyskuuta 1750 hän luki Berliinin akatemian edessä muistomerkin, jossa hän esitti periaatteen "voima on yhtä suuri kuin massa kertaa kiihtyvyys" Eulerin jäykän kehon pyörimisen yhtälön yhteydessä omana uutena löytönään. Kuitenkin vasta vuonna 1775 Euler julkaisi kulmamomentin lain yleisimmin voimassa olevassa muodossaan itsenäisenä uutena mekaanisena periaatteena. Johtuen Bernannlin ajatuksesta teoksessaan Hydraulica ja leikkausperiaatteen soveltamisesta äärettömän pieneen tilavuuselementtiin, Euler sai mekaniikan impulssiperiaatteen ,
toisin sanoen nykyään niin yleinen “ voima = massa × kiihtyvyys ”, joka johtuu aina Newtonista, mutta jota ei löydy sieltä tässä muodossa.
Nestemekaniikka

Historiallisesti merkittäviä edistysaskeleita teoreettisessa nestemekaniikassa tekivät 1700-luvulla Jean d'Alembert, Daniel Bernoulli, Alexis Clairaut ja Joseph Lagrange . Näiden suurten matemaatikkojen joukossa Euler pani tärkeimmän panoksen nestemekaniikkaan perustamalla kuuluisat liikeyhtälöt, nestemekaniikan Eulerin yhtälöt .
Eulerin päätyö nestemekaniikan alalla perustui pääosin jatkumohypoteesiin ja Newtonin liikelakiin . Hänen työnsä muodostaa pohjan nestemekaniikan matemaattiselle teorialle, joka sisältyi hänen löytöönsä vaihteluiden ja osittaisten differentiaaliyhtälöiden laskennasta . Hän antoi perustavanlaatuisen panoksen hydrostaatikaan ja hydrodynamiikkaan vuosina 1752–1761 ja julkaisi vuonna 1757 useita tärkeitä artikkeleita näillä alueilla Mémories de l'Academie des Sciences de Berlin . Ensimmäisessä näistä artikkeleista tarkasteltiin nesteiden perusperiaatteita, periaatteita ja tasapainoyhtälöitä . Toinen ja kolmas opinnäytetyö käsittelivät pääasiassa massayhtälön (tai jatkuvuuden yhtälön) säilyttämistä ja kokoonpuristuvien nestevirtojen epälineaarisia Euler-yhtälöitä. Sitten hän muotoili liikkeen yhtälöt ja jatkuvuuden yhtälön ei-viskoosille , puristamattomalle nestevirtaukselle ensimmäisellä todisteella kuuluisasta d'Alembertin paradoksista ei-viskoosisessa nestevirtauksessa, joka virtaa jäykän rungon ohi.
Lisäksi Leonhard Euler toiminut mekaniikan aloilla ja turbiinin yhtälön ja gyroskooppiseen teoria , jossa hän esitteli Euler kulmat on lisäksi Eulerin yhtälöt . Häntä pidetään maailman ensimmäisen vesiturbiinin kehittäjänä. Euler-turbiinin jälleenrakennus osoitti, että sen 71%: n hyötysuhde on vain hieman alle nykyaikaisten turbiinien (vuodesta 2015). Juoksupyörän käytön ja aluksen potkurin teknisesti toteutettavissa oleva periaate johtuu myös Euleristä.
Tekninen mekaniikka
Ensimmäinen analyyttinen kuvaus puristusvoimalla kuormitetun tangon taipumisesta palaa myös Euleriin; hän perusti vakauden teorian . Hän auttoi kehittämään Euler-Bernoullin palkki yhtälö , josta tuli kulmakivi engineering.
tähtitiede
Sen lisäksi, että Euler sovelsi menestyksekkäästi analyyttisiä työkalujaan klassisen mekaniikan ongelmiin, Euler käytti niitä myös tähtitieteessä - tämä työ tunnustettiin koko uransa ajan useilla Pariisin akatemian palkinnoilla. Hänen saavutuksiinsa kuuluu komeettojen ja muiden taivaankappaleiden kiertoradan tarkka selvittäminen, komeettojen luonteen ymmärtäminen ja aurinkoparallaksin laskeminen . Hänen laskelmansa auttoivat kehittämään tarkkoja pituusasteitaulukoita .
Mukaan Victor J. Katz , on varmaa, että Euler oli ensimmäinen matemaatikko Euroopassa järjestelmällisesti tunkeutua hammaskiven trigonometriset funktiot. Hän teki tämän teoksissa, jotka ilmestyivät vuodesta 1739 eteenpäin. Hän sai tietää, että on tärkeää trigonometriset funktiot muutamaa vuotta myöhemmin, kun hän pyrki ratkaisemaan tiettyjä differentiaaliyhtälöt , etenkin lineaariset differentiaaliyhtälöt kanssa vakiokertoimiset . Takautuvasti ilmeinen tosiasia, että trigonometrisillä funktioilla laskeminen on avain "jaksollisten ilmiöiden", mukaan lukien planeettojen ja satelliittien liikkeet, ymmärtämiseen , ei näytä olevan ilmeistä tähtitieteilijöille ennen Euleria. Euler oli ensimmäinen, joka käsitteli häiriöongelman muotoilua ja ratkaisua - avainongelma, joka oli muotoiltava ja ratkaistava, jos Newtonin painovoimalaki oli tarkoitus perustaa planeetan ja kuun teorian perustaksi .
Laskemalla trigonometriset toiminnot kädessä, hän rakensi sarjan kuun taulukoita. Nämä julkaistiin hänen Opuscula varii argumenti -kirjassaan vuonna 1746 . Eulerin ensimmäinen yritys selviytyä planeetan häiriöistä tuli vastauksena Pariisin akatemian palkintokilpailuun vuonna 1748. Palkinto myönnettiin " Jupiterin ja Saturnuksen teoriasta, joka selittää eriarvoisuuden, jonka nämä planeetat aiheuttavat liikkeissään, vaikuttavat erityisesti ajoitukselta. niiden yhteyteen ”. Newton oli kirjoittanut hänen Principia of "häiriön kiertoradalla Saturnuksen jokaisessa yhdessä tämän planeetan", "joka on niin herkkä, että tähtitieteilijät ovat tappiolla". Vastauksena Pariisin akatemian vuoden 1748 palkintojen arvontaan Euler kirjoitti kaksi muistikirjaa, jotka molemmat valmistuivat vuoden 1747 puolivälissä. Ensimmäisessä, jonka Euler esitteli Berliinin akatemialle, hän johti differentiaaliyhtälöt häiriöiden ongelmaan. Toinen, johdannainen Jupiterin Saturnuksen häiriöistä, ilmoittautui kilpailuun ja voitti palkinnon, vaikka Euler ei selittänyt Saturnuksen ilmeistä hidastumista tai Jupiterin kiihtyvyyttä. Eulerin palkinto-essee teki vaikutuksen innovatiivisiin menetelmiin, jotka hän esitteli planeetan häiriöiden käsittelemiseksi.
optiikka
Vuonna optiikka , hän julkaisi teoksia aalto teorian valossa ja laskennan optisten linssien välttää värivirheitä . Hän ristiriidassa Newtonin corpuscle teoria valon Opticks , joka vallitsi tuolloin. Hänen työnsä optiikan parissa 1740-luvulta vaikutti siihen, että Christiaan Huygensin ehdottama valoaaltoteoria tuli hallitsevaksi ajattelutavaksi ainakin valon kvanttiteorian kehittämiseen saakka.
Lähes suurin osa Eulerin optiikkaa koskevista kirjoituksista, yhteensä seitsemän viidestätoista, on omistettu hajonta- kysymyksille . Muun muassa hän oli toistuvasti huolissaan siitä, onko punaisella vai violetilla korkeampi taajuus . Euler muutti näkemystään tästä kolme kertaa, joka kerta teoreettisen pohdinnan perusteella, jonka hänen kuulemansa uusi koe oli saanut hänet tekemään. Vuonna nova Theoria , punainen yhä oli suurin taajuus, kahden myöhemmin toimii korjasi tämän näkymän perustuu muun muassa hänen teoriansa havainnoimalla värien ohuita. Mutta sitten, kun otetaan huomioon metallilamellien joustavuus , se palautetaan ensimmäiseen, väärään näkymään ja sitten lopulta oikeaan.
ballistiikka
Vuonna 1745 Euler käänsi englantilaisen Benjamin Robinsin teoksen Tykkimiehen uudet periaatteet saksaksi. Se ilmestyi Berliinissä samana vuonna otsikolla Uudet tykistön periaatteet, joka sisälsi jauheen voiman määrittämisen sekä tutkimuksen ilman vastuksen (sic) erosta ( sic ) nopeissa ja hitaissa liikkeissä. Koska Galileo , artillerymen oli katsottu liikeradat ammukset parabolas, ottaen huomioon ilmanvastus olevan vähäinen. Robins suoritti yhden ensimmäisistä ballistiikkakokeista ja osoitti, että ilmanvastus vaikuttaa merkittävästi lentoreittiin. Robinsin ja Eulerin avun ansiosta luotiin ”ensimmäinen ballistiikan oppikirja”. Esimerkiksi se otettiin käyttöön Ranskassa virallisena oppikirjana sotilaskouluissa. Napoleon Bonaparten täytyi opiskella sitä luutnanttina.
laivanrakennus
Vähemmän tunnettuja ovat Eulerin teokset alusten vakavuuskriteeristä , joissa hän uudisti tiedon, jonka Archimedes oli jo hankkinut, mutta menetti uudelleen . Scientia navalis , tärkein työ laivanrakennus, joka odotetaan pitkälle 19th century, ilmestyi alkuvuosina Berliinissä.
algebra

Algebrassa Euler työskenteli muun muassa yhtenäisyyden juurien nimenomaisessa muodossa . Nämä esiintyvät ratkaisuina yhtälöihin . 1700-luvulla pidettiin uraauurtavana ongelmana ilmaista näiden yhtälöiden ratkaisut algebrallisella tavalla "radikaaleja" käyttäen. Euler menestyi myös tällä alalla ja ratkaisi yksikköyhtälöt asti . Teknisesti erityisen vaikea on menetelmä , jolla ratkaisut ilmaistaan neliö- ja kuutiojuurina .
Euler tutki intensiivisesti muodon Diophantine-yhtälöitä ja missä ovat kokonaislukuja eikä neliönumeroa. Suuremmalla yleisellä tasolla hän tutki tyypin yhtälöitä
missä erotin ei ole neliö.
Euler kehitti likimääräiset menetelmät numeeristen yhtälöiden ratkaisemiseksi ja työskenteli myös - todennäköisesti Daniel Bernoullin ehdottaman - eliminointiongelman kanssa . Hän onnistui osoittamaan Newtonin jo tunnetun lauseen, jonka mukaan kahdella m- tai n- asteen algebrallisella käyrällä voi olla enintään mn- leikkauspiste . Tässä yhteydessä hän tuli tärkeään tuloksen käsitteeseen . Kahdessa asiakirjassa E147 ja E148 vuodelta 1750 Euler selitti perusteellisesti niin sanotun Cramer-paradoksin .
Vuonna 1770 hän toi esiin kirjan Complete Guide to Algebra . Hän kehitti menetelmän kvartaalisten yhtälöiden ratkaisemiseksi . Euler myös huomannut, että yleensä , quintic yhtälöitä ei enää voida ratkaista radikaalit ( toisin sanoen suljettu ketjuja juuri ilmaisuja ). Niels Henrik Abel ja Évariste Galois kuitenkin todistivat tämän tuloksen vasta myöhemmin .
logiikka
Eulerille hyvitetään myös suljettujen käyrien käyttämistä sylogistisen päättelyn havainnollistamiseksi . Nämä kaaviot tunnetaan nimellä Euler-kaaviot. Helmikuussa ja maaliskuussa 1761 kirjoitetut kirjeet 101-108 (saksalaiselle prinsessalle) esittävät kaaviot, jotka nyt tunnetaan nimellä Venn-kaaviot, vaikka tämä onkin väärä nimi. Kaaviot logiikan matemaattisista esityksistä ilmestyivät joissakin 1700-luvun aiheeseen liittyvissä tutkielmissa, ja on mahdollista, että Johann Heinrich Lambert käytti niitä vähän ennen Eulerin kirjeitä. Kirjeissä 101 ja 102 Euler korosti kurinalaisen kielen tarvetta esitettäessä yleisiä ideoita ja niiden laajentamista; hän käytti ympyröitä kaavioissa selittääkseen syllogismien ja hypoteettisten ehdotusten eri muotoja .
Euler-kaavio on kaaviomainen tapa näyttää joukot ja niiden suhteet. Euler-kaaviot koostuvat yksinkertaisista suljetuista käyristä (yleensä ympyröistä tai ellipseistä ) tasossa, joista kukin edustaa suuruuksia. Jokainen Euler-käyrä jakaa tason kahteen alueeseen tai "vyöhykkeeseen": sisäalue, joka sisältää symbolisesti joukon elementit ja edustaa sitä, ja ulompi alue, joka edustaa kaikkia elementtejä, jotka eivät kuulu joukkoon ( komplementti ). Käyrien koot tai muodot eivät ole merkityksellisiä. Kaavio on tarkoitettu vain havainnollistamaan niiden päällekkäisyyttä. Kunkin käyrän rajoittamien alueiden (päällekkäisyys, eristäminen tai kumpikaan) alueelliset suhteet vastaavat joukko-teoreettisia suhteita ( leikkaus , osajoukko ja disjunktiivisuus ). Käyrät, joiden sisävyöhykkeet eivät leikkaa, edustavat disjointijoukkoja.Kaksi käyrää, joiden sisävyöhykkeet leikkaavat, edustavat joukkoja, joilla on yhteisiä elementtejä (ei- tyhjä leikkauspiste): Molempien käyrien sisällä oleva vyöhyke edustaa elementtijoukkoa, nämä kaksi joukkoa ovat yhteisiä. Käyrä, joka on kokonaan toisen alueella, edustaa niiden osajoukkoa.
Euler-kaaviot (ja yleisemmät Venn-kaaviot ) sisällytettiin uuden matematiikan kurssille osana joukko-teorian opetusta 1960-luvulta .
Kartografia ja geodeesia
Euler osoitti suurta kiinnostusta tähtitieteellis-geodeettisiin ja kartografisiin kysymyksiin, joiden ratkaisemiseksi perustettiin uusi tiedeinstituutio Pietarin tiedeakatemiaan Joseph-Nicolas Delislen ehdotuksesta - ns. Maantieteellinen osasto . Euler työskenteli siellä Delislen avustajana useita vuosia. Katsaus tämän osaston useisiin asiakirjoihin, erityisesti protokolliin, paljasti monia yksityiskohtia Eulerin työstä geodeesian ja kartografian alalla . Joten voisiko z. Esimerkiksi voidaan todeta, että Eulerin asema maantieteen laitoksella oli täysin hänen toiveidensa ja tieteellisten taipumustensa mukainen. Eulerin ensimmäinen työ oli senaatin pyytämä kartta Venäjän Euroopan rajoista. 2. syyskuuta Euler neuvotteli Delislen kanssa parhaasta tavasta rakentaa tällainen kartta. Euler valmisti Venäjän Euroopan rajojen kartan 6. syyskuuta 1736. Vasta 14. lokakuuta 1736 Euler ja Delisle olivat aloittaneet yhdessä, kun dosentti Vasily Evdokimowitsch Adodurow oli tehnyt korjaukset .
Matemaattinen musiikkiteoria
Myös musiikkialalla Eulerin ajatukset perustuivat pääasiassa matematiikkaan: hän perusti musiikkiteorian, joka perustui matemaattisiin laeihin (mukaan lukien Tentamen novae theoriae musicae , 1739, Music mathématique, Pariisi 1865). Hänen malli ääni verkko on yhä käytössä laskelmissa puhdasta viritys . Vaikka hänen musiikkiteorian kirjoituksensa muodostavat vain pienen osan hänen työstään (muutama sata sivua, noin 30 000 sivun kokonaistuotannosta), ne kuitenkin heijastavat varhaista kiinnostusta, joka ei ole jättänyt häntä koko elämäänsä.
Eulerin musiikkiteorian ymmärtämiseksi on tiedettävä, että musiikilliset intervallit ns. Puhtaassa virityksessä sävelkorkeuden oktaavin, viidennen , neljännen ja suuren kolmanneksen kanssa, jotka vastaavat taajuussuhteita 1: 2, 2: 3, 3: 4 tai 4: 5 rakennettavaan perustavanlaatuiseen . Päinvastoin, nykyään on yleisin yhden tason viritys (hyvin temperoitu), jossa kahdella puolisävyn sävyllä on aina tarkka taajuussuhde .
Martin Vogel toteaa: "Leonhard Euler järjesti erittäin hyödyllisen ja käytännöllisen konsonanssiasteen laskennan." Hän jatkaa, "että tulokset ovat suurelta osin yhtäpitävät hyvien psykologisten testien kanssa. Siitä voidaan tehdä tärkeitä johtopäätöksiä säveltämisen ja analysoinnin käytännön työstä ”. ”Euler olettaa, että ihmiset haluavat elää järjestäytyneessä maailmassa ja että tämän, ei liian rasittavan, järjestyksen ymmärtäminen lisää heidän hyvinvointiaan. ... Euler totesi edelleen: Mitä yksinkertaisempi suhde on, sitä pienempiä lukuja se ilmaistaan, sitä selkeämmin se voidaan havaita ja sitä miellyttävämpi on sen vaikutus. ”Euler yrittää nyt määritellä tämän yksinkertaisuuden tarkemmin ja käyttää sitä se ymmärtää matemaattisissa kaavoissa, että se vastaa mahdollisimman hyvin kuulovaikutelmaa. Hän käyttää alkulukuteorioita.
Ensinnäkin Euler määrittelee konsonanssit, ts. H. Harmoniat, "tutkinto". Tämän on tarkoitus matemaattisesti kaapata sävyjen harmonian "vaikeus". Matala taso puhuu "hyväksyttävästä" - korkea taso "epämiellyttävästä" äänestä. Funktiona Euler käytti suavitatis- astetta ("rakkauden, yhteensopivuuden aste") , joka voidaan tulkita puhtaasti abstraktisti numeroteoreettisena funktiona : Luonnolliselle luvulle n, jonka alkutekijä on, se määritetään
Gradus suavitatis edustaa siis luonnollisten lukujen alkutekijän arviointia ja on suurempi, sitä suuremmat alkuluvut ja sitä suuremmat niiden eksponentit. Kaksi sointua luokitellaan nyt seuraavasti: Suhteelle a : b , missä se on jo kokonaan lyhennetty, so. ts. a ja b ovat kopriimi , yksi sarja
Euler soittaa numero (vähiten yhteisen jaettavan ja b ) eksponentti on : b . Esimerkiksi täydellisen viidennen asteen on 4, koska se pätee . Tämä periaate voidaan laajentaa mihin tahansa sointuihin käyttämällä kokonaisäänen LCM: ää. Jos kolmikko a: b: c , jossa , b ja c ovat kukin prime, yksi on esimerkiksi . Eulerin perustelut selittävät esimerkiksi, miksi pääkolmikko (kuten CEG, suhteessa 4: 5: 6) kuulostaa ”onnellisemmalta” kuin pienikokoinen kolmikko (EGH, suhteessa 10:12:15). Suunnitelmassa päätriaadilla on yhdeksäs ja sivutriadilla neljästoista - ala-kolmikko on "surullisempi", koska "ilo asioista, joiden järjestys on yksinkertaisempi ja helpommin havaittavissa, ja suru asioista, joiden järjestys on monimutkaisempi" ja vaikeasti havaittavissa ”. Joten Euler käytetään periaatetta eksponentti jotta ehdottaa derivaatiota gradus suavitatis Intervallitoistojen sointuja niiden päätekijöitä - täytyy kantaa mielessä, että aluksi hän vain käytti viides-kolmas järjestelmä , so H. otti huomioon 1, 2 ja alkuluvut 3 ja 5. Edellä mainittua gradienttitoimintoa, joka laajentaa tämän järjestelmän mihin tahansa määrään alkulukuja, ehdotettiin myöhemmin.
Näiden laskelmien tulosten osalta Vogel totesi: "Eulerin järjestelmä ei ole täysin samaa mieltä tavallisista aikavälien käsityksistä. Mutta kuka tahansa, joka ymmärtää, miten nämä ideat syntyivät ja kuinka perusteeton teoria, johon ne perustuvat, sanoo itselleen, että ei voi olla toisin, että uusi lähestymistapa, jonka on tarkoitus viedä meitä pidemmälle, ei voi olla sama vanhoihin kappaleisiin. Eulerin tutkinnot eivät aina vastaa yleisiä odotuksia, mutta ne vastaavat melko hyvin kuulovaikutelmaa. "
Vaikka perinteinen musiikkiteoria olettaa usein selkeän rajan konsonantti- ja dissonanttivälien välillä , Euler näyttää vain asteittaisia eroja, ts. Hienoja porrastuksia kahden samanaikaisesti soivan nuotin eri sulautumisasteiden välillä. Tämän avulla hän ottaa uuden musiikin tärkeän periaatteen , esim. B. von Schönberg , ensinnäkin, jossa konsonanssin ja dissonanssin välinen perusraja ei enää ole voimassa.
Luvussa "Eulerin rajat" Vogel yrittää tehdä uskottavaksi, että Eulerin kaavojen soveltaminen kolmiosaisiin ja moniäänisiin sointuihin ei johda merkityksellisiin tuloksiin. Toisaalta Vogel painottaa kaksiosaisia sointuja (= intervalleja): "Intervallien käytännön käytössä Eulerin luokitus osoittautuu kuitenkin erittäin hyödylliseksi. Tämä havainto korostaa käytännön puolta. Teoreettinen perustelu olisi vaikeaa, ellei mahdotonta. "
Eulerin konsonanssiteoriaa on kuitenkin täydennettävä hänen korvausteorialla: kuunnellessamme musiikkia, jonka intonaatio poikkeaa hieman ihanteesta, hänen mielestään emme havaitse sisäisen mielikuvituksen sävelkorkeuksia niin paljon kuin mahdollista, vaan niitä, jotka ovat enemmän ihanteellisen toiveemme mukaisesti. ”Korva kuulee oikein. Korva kuulee taloudellisesti. Se kuuntelee perustellusti esitettyjä välejä yksinkertaisimpien mittasuhteiden mukaisesti. Korva tunnistaa oikeastaan tarkoitetun välin, aivan kuten silmä hyväksyy suorakulmaisen kolmion taululle ja näyttää, vaikka sen kulma ei olisikaan oikea. "Tämä mitätöi syytöksen, jonka Eulerin konsonanssilaskelmat kohtaavat usein:" Eulerin teoria värähtelyrytmejä on usein hylätty halvalla vastaväitteellä, jonka mukaan pieni viritys riittäisi muuttamaan puhtaimman konsonanssin karkeimmaksi dissonanssiksi. Puhtaan viidennen 300/200: n sijasta täytyy vain olettaa 301/200: n viritys, jotta saadaan suhde, jota ei enää voida havaita. Euler vastusti tällaista vastustusta korvausteorialla, mistä hänen kriitikonsa eivät useimmiten ole tietoisia. Olkoon riittävän todistettu, että henkisesti tarttuva sävysuhde eroaa usein akustisesti annetusta suhteesta. Tällaisissa tapauksissa havaittu osuus on yksinkertaisempi kuin todellinen. Ero on niin pieni, että se välttää käsityksen. Korva on tottunut hyväksymään yksinkertaisemman numeerisen suhteen, joka poikkeaa siitä vain vähän. "
"Kuitenkin Eulerin teos kuuntelemisesta yksinkertaisimmilla ehdoilla ei ole lupa epäpuhtaalle musiikin tekemiselle ja huonolle intonaatiolle. Euler ei jätä epäilystäkään siitä, että olisi pyrittävä korkeimpaan mahdolliseen puhtausasteeseen. Mitä helpompi on tarttua väleihin, sitä vähemmän väsynyt korva ja sitä suurempi nautinto musiikista. "
Kuuntelun periaate perustuu myös karkaistujen viritysjärjestelmien käyttöön , koska niitä käytetään usein musiikissa, erityisesti kosketinsoittimien kanssa.
Toinen lähestymistapa Eulerin musiikkiteoriassa on niin kutsuttujen "tyylilajien" määrittely, ts. H. mahdollisia osa-alueita, joka oktaavin että alkulukuja 3 ja 5. Nämä ovat peräkkäisiä ääniä, jotka noudattavat tiettyjä taajuuden suhteet ja ovat siksi asteikot . Euler kuvaa 18 tällaista sukua, jotka perustuvat alkulukuihin 3 ja 5. Menettely on seuraava: Jokainen tuote kuvaa perustaajuuden kerrannaisjärjestyksen - otetaan kaikki mahdolliset jakajat . Esimerkiksi yhdellä on suhteet 1: 1, 1: 2, 1: 3, 1: 5, 1: 6, 1:10, 1:15, 1:30. Koska luku 2 (oktaavia lukuun ottamatta) ei kuitenkaan muuta mitään esiintyvissä äänissä (taajuuden kaksinkertaistaminen määrittelee oktaavihypyn), kahden voimalla ei ole merkitystä genren kannalta.
Euler esitteli tyylilajeitaan pienikokoisissa taulukoissa, jotka asettavat visuaalisesti musiikilliset ja matemaattiset merkinnät. Hän osoitti, kuinka tärkeitä molemmat olivat hänelle ja kuinka hän yritti saada heidät yhteen:
Tätä periaatetta kehitti edelleen Adriaan Fokker . Esimerkiksi tapaus voidaan normalisoida seuraaviin oktaavin suhteisiin: 1: 1, 8: 9, 16:21, 2: 3, 4: 7, 32:63.
Tyylilajit 12 (Eulerin kanssa ), 13 (Eulerin kanssa ) ja 14 (Eulerin kanssa ) ovat korjattuja versioita diatonisista , kromaattisista ja enharmonisista versioista muinaisista ajoista. 18. suku ( ) on "diatonikromaattinen", "jota käytetään yleensä kaikissa koostumuksissa" ja joka osoittautuu identtiseksi Johann Matthesonin kuvaaman järjestelmän kanssa. Euler näki myöhemmin mahdollisuuden kuvata sukuja, mukaan lukien alkuluku 7. Euler kehitti erityisen kaavion, Speculum musicum , kuvaamaan diatoninen-kromaattinen genre, ja selitti tämän kaavion polut tietyille aikaväleille, mikä muistuttaa hänen kiinnostustaan graafiteoriasta, erityisesti Königsbergin seitsemästä sillasta. Konsepti herätti uutta kiinnostusta ääniverkostona musiikkiteoreetikko Hugo Riemannin mukaan nimettyyn uus-Riemannin teoriaan (Neo-Riemannin teoria) .
Suosittuja esityksiä ja teemoja
Eulerin suosittu tieteellinen tutkielma Lettres à une princesse d'Allemagne vuodelta 1768, jossa hän kirjoitti kirjeitä prinsessa Friederike Charlotte von Brandenburg-Schwedtille , Frederick II: n veljentytärlle, sai tietää fysiikan ja tähtitieteen perusteista, sai erityisen suuren yleisön merkityksen. joka opetti matematiikkaa, filosofiaa ja teologiaa. Euler aloitti ensimmäisen kirjeen selittämällä termi " koko " (la grandeur) . Perustuen määritelmä jalka , hän määritteli mailin ja motivoitunut eri ulottuvuuksien käytännön esimerkein. Joten on parempi asettaa Berliinin ja Magdeburgin välinen etäisyys 18 mailiin (yksi käännös puhuu 83 englanninkielisestä mailista ) 432 000 jalan (43,824 jalan ) sijaan. Myöhemmät kirjeet sisälsivät optiikkaa, magnetismia, sähköä, mutta myös tähtitiedettä. Muun muassa Euler arvioi maan ja auringon väliseksi etäisyydeksi "trente Millions de Milles" (kolmekymmentä miljoonaa mailia).
Alunperin ranskaksi kirjoitettujen 234 kirjeen kaksi ensimmäistä osaa julkaistiin Pietarissa vuonna 1768 ja kolmas Frankfurtissa vuonna 1774. Kirjeet painettiin myöhemmin uudelleen Pariisissa, ensimmäinen osa vuonna 1787, toinen vuonna 1788 ja kolmas vuonna 1789. Pariisissa vuonna 1787 julkaistu Lettresin ensimmäinen painos sisälsi Eloge de M.Eulerin , joka on 36 sivun nekrologi. kirjoittanut markiisi de Condorcet , joka antoi lukijalle elämäkerrallisen Luonnokset ja kohokohdat Eulerin urasta. Vaikka Euler kirjoitti kirjeet ranskaksi, pidetään varmana, että Condorcet teki joitain toimituksellisia muutoksia, koska teksti eroaa alkuperäisestä.
Euler omistautui myös shakkimatematiikkaan , esimerkiksi ritari- ongelmaan . Tämä koskee kysymystä siitä, onko mahdollista, että ritari- shakkikappale kulkee shakkilaudan jokaisen neliön läpi täsmälleen kerran edestakaisen matkan aikana. Euler mainitsi ongelman kirjeessään Christian Goldbachille vuonna 1757. Vuosina 1758-1759 hän kirjoitti lopulta aiheesta paperin, joka julkaistiin vuonna 1766 Berliinin memoireissa .
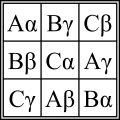
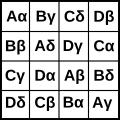
Hän pidetään keksijä kreikkalais-latinalaisen neliön , edeltäjä Sudoku . Tämä on (järjestyksessä n ) neliö n x n -malli, jonka kenttiin kahden ( n -elementin ) joukon elementit syötetään siten, että tarkalleen yksi kopio kustakin elementistä näkyy jokaisessa sarakkeessa ja rivissä. Esimerkkejä ovat:
Työssään Recherches sur une nouvelle espece de quarres magiques Euler antaa satoja esimerkkejä tällaisista neliöistä ja käsittelee myös neliöitä, joiden diagonaalit täyttävät vaaditun ominaisuuden. Loppujen lopuksi hän väittää toimittamatta tarkkoja todisteita siitä, että kreikkalais-latinalaista neliötä, jonka koko on 4 k + 2, ei voida rakentaa. Vasta vuonna 1960 paljastettiin, että Euler oli väärässä. Kreikan ja latinan neliöitä on aina olemassa lukuun ottamatta järjestyksiä 2 ja 6. Algebrallis-algoritmisessa rakentamisessa käytettiin ryhmäteoriaa , äärellisiä kappaleita , projektivista geometriaa ja lohkosuunnitelmia .
Arkistoidun kartanon käsittely
Postuuminen julkaisuprosessi
Eulerin kuoleman jälkeen Pietarin akatemia julkaisi Eulerin aiemmin julkaisemattomat teokset Mémoireissaan postuumisti . Julkaisujen suuren määrän (noin 100 artikkelia) vuoksi julkaisuprosessi julistettiin päätökseen vasta vuonna 1830. Mutta pian kävi ilmi, että Euler oli kirjoittanut muita papereita. Kun Paul Heinrich von Fuss oli tullut Pietarin akatemian sihteeriksi isänsä seuraajana vuonna 1825, hän tutki sen arkistoja ja löysi muun muassa paketteja Eulerin kirjeenvaihdosta. Bernoullien kanssa. Tästä kasvoi kirjeenvaihdon hakemisto kahdessa osassa otsikolla Correspondance mathématique et physique de quelques céleèbres géomètres du XVIIIème siècle . Tähän liitettiin luettelo Eulerin kirjoituksista. Sen jälkeen kun Fussin isä Nikolaus -hakemisto ei vielä sisältänyt 700 numeroa, se on nyt laajennettu 756: een. Jatkokäsittelyä varten arkistoja etsittiin uudelleen ja teos, jota ei vielä julkaistu, tuotettiin nimellä Astromania mechanica .
Koko teoksen julkaiseminen
Ensimmäiset yritykset 1800-luvulla
Ensimmäiset yritykset julkaista Eulerin kokonaisia teoksia ovat peräisin 1830-luvulta. Aloitteita oli lähinnä kaksi. Yhden heistä loi Paul Heinrich Fuss. Vaikka monet tunnetut matemaatikot, mukaan lukien Carl Gustav Jacobi , kannustivat Fussia , projekti lopulta hylättiin, kun se osoittautui akatemian budjetin taloudellisten mahdollisuuksien ylittäväksi. Ainoa tulos Fussin ja Jacobin aloitteesta oli kahden Commentationes arithmeticae -nimikkeen julkaiseminen vuonna 1849, joka koostui 94 jo julkaistusta artikkelista ja viidestä julkaisemattomasta käsikirjoituksesta. Samanaikaisesti ryhmä belgialaisia matemaatikkoja ryhtyi vastaavaan projektiin. He menestyivät paremmin kuin Fuss ja Jacobi siinä, että tätä painosta viisi painosta todella painettiin. Tätä painosta on arvostellut ankarasti erityisesti belgialainen matemaatikko Henri Bosmans , joka kuvaili sitä "erittäin huonoksi teokseksi". Jotta Eulerin teokset olisivat saatavissa suurelle yleisölle, toimittajat olivat muuttaneet alkuperäisiä tekstejä, jotkut mielivaltaisesti, vaikka alkuperäinen olisi jo kirjoitettu ranskaksi. Muiden matemaatikkojen helppo pääsy nähdään toimittajien liikkeellepanevana voimana, ja teoksella pitäisi vielä olla "stimuloiva vaikutus" heihin nykyään.
1900-luvun alku
1900-luvun alussa Venäjän tiedeakatemia käynnisti uuden aloitteen Eulerin kokonaisen teoksen julkaisemiseksi, joka merkitsee Eulerin syntymäpäivän kaksikymmentä vuotta. Aikaisempien yritysten epäonnistumisen edessä venäläiset etsivät liittolaisia, joiden kanssa he voisivat jakaa työvoimaa ja kustannuksia; instituutio, joka tuli mieleen Eulerin suhteen, oli Preussin tiedeakatemia Berliinissä, jota Euler oli palvellut 25 vuotta. Berliinin tutkijat olivat alun perin melko innostuneita tästä suunnitelmasta. Mutta kun kävi ilmi, että Venäjän akatemia halusi jakaa tehtävänsä julkaista matemaattinen ja fyysinen korpus ja vaatia entistä itselleen, innostus heikkeni. Preussin akatemia pyysi jäsentensä arvostetuinta fyysikkoa Max Planckia arvioimaan ehdotuksen. Kuuluisassa lausunnossa Planck sanoi, että voi olla totta, että matemaatikot ovat edelleen innoittamana Eulerin kirjoituksista, mutta fyysikot eivät ole samassa määrin. Hän epäili, että Eulerin fyysisten kirjoitusten julkaiseminen "ei ollut fysiikan etuja aikamme tiede" ja kieltäytyi siksi sallimasta Preussin akatemian osallistumaan projektin rahoittamiseen. Koska täydellinen painos oli liian kallis Venäjän akatemialle, tämä aloite päättyi myös epäonnistumiseen.
Gustaf Eneströms Euler -hakemisto
Vuosina 1910–1913 ruotsalainen matemaatikko Gustaf Eneström loi hakemiston, joka sisälsi kaikki Eulerin teokset. Tässä on 866 numeroa, jotka on järjestetty periaatteen E001, ..., E866 mukaisesti.
Euler-komission ja Opera omnia -säätiön perustaminen
1800-luvulla epäonnistuneiden yritysten jälkeen Leonhard Eulerin 200. syntymäpäivä huhtikuussa 1907 oli syy Sveitsin luonnontieteelliselle seuralle perustaa toinen täydellinen painos Eulerin julkaisuista. Aloitteen sai matemaatikko Ferdinand Rudio , joka oli matematiikan professori Zürichin ammattikorkeakoulussa (nykyinen ETH Zürich ). Tulipuheessa Eulerin 200. syntymäpäivän juhlissa, joka pidettiin Baselissa lukemattomien ulkomaisten tutkijoiden läsnä ollessa, Rudio vetoaa taitavasti sveitsiläiseen isänmaallisuuteen ja kansainväliseen solidaarisuuteen: Eulerin kotimaalle "teosten julkaiseminen on kunniavelvoite" Sveitsi kuitenkin tarvitsee "kahden maan, jossa Euler tuli kuuluisaksi ja kunniaksi", Saksan ja Venäjän tukea:
"Sveitsissä säilyy aina kiitollisuuden tunne Pietarin ja Berliinin akatemioille, jotka he ovat antaneet Eulerillemme, jolle hänen oma isänmaansa oli liian pieni, isompi ja antanut hänelle mahdollisuuden täydentää suurta elämäntyötään väärentämättömällä luovuudella. "
Rudion sanat saivat voimakkaan resonanssin kaikkialla. Schweizerische Naturforschende Gesellschaft perusti yrityksen johtamiseksi Euler-komission , jonka puheenjohtajaksi valittiin Rudio. Nuoren komission ensimmäinen toimi oli vetoomus lahjoituksiin. Lupauksen taloudellisesta tuesta tuli myös Pietarin akatemiasta. Tämä tarjosi myös "asettaa kaikki arkistoissaan olevat materiaalit saataville yrityksen parhaan mahdollisen toteuttamisen kannalta". Vuosina 1910–1912 koko Eulerin kartano saapui Sveitsiin seitsemässä laatikossa diplomaattipostina Venäjän suurlähetystön kautta. Vaikka työ (jota tukivat tunnetut matemaatikot, kuten Aleksanteri Ljapunov ) eteni alun perin nopeasti, Euroopan poliittiset erimielisyydet vaikuttivat Eulerin komissioon. Sveitsissä oli huomattavia varaumia Neuvostoliiton kommunistijärjestelmää vastaan, ja vuosina 1918–1946 näiden kahden valtion välillä ei ollut minkäänlaista diplomaattista suhdetta. Tutkijoilla oli kuitenkin edelleen vaikeampi yhteys. Vaikka Venäjän osapuoli hyväksyi 28. toukokuuta 1921 pyynnön "sotaan liittyvien ongelmien" viivästymisestä, Pietarin akatemia vaati vuonna 1930 käsikirjoituksia takaisin. Eulerin komissio kieltäytyi vastaamasta tähän pyyntöön, mikä herätti vilkasta kirjeenvaihtoa. Sveitsin puoli yritti aluksi useilla argumenteilla viivästyttää toistuvasti käsikirjoitusten palauttamista. Heinäkuussa 1930 Neuvostoliiton akatemia sopi, että käsikirjoitusten tulisi pysyä Zürichissä "jonkin aikaa", ja pyysi tarkkaa aikataulua jäljellä olevien määrien julkaisemiselle. Sen jälkeen, kun Andreas Speiser ei suostunut Venäjän pyyntöön palauttaa ainakin ne käsikirjoitukset, joita ei enää tarvittu , ääni tuli terävämmäksi. Neuvostoliiton akatemia itse asetti määräajan 5. kesäkuuta 1933:
"Neuvostoliiton tiedeakatemialla on kunnia ilmoittaa teille, että tiedekomitea. ja Moskovan keskuskomitean oppilaitokset ovat tunnustaneet tarkoituksenmukaiseksi säilyttää Eulerin käsikirjoituksia Zürichissä kahden vuoden ajan tämän päivän päivämäärästä. "
Vaikka komissio alun perin suostui näihin vaatimuksiin, sen oli selvitettävä ensi vuonna, että aikataulua ei voitu noudattaa. Speiser kirjoitti epäonnistuneessa vetoomuksessa Sveitsin poliittisen osaston johtajalle Giuseppe Mottalle , että "tämän julkaisun [...] pitäisi kestää vähintään kaksikymmentä vuotta". Venäjältä tulevan lisäpainamisen seurauksena aloitettiin myös kopioiden ja valokuvien tuotanto. Tämä valmistui vuonna 1938. Asiakirjojen lopullinen luovutus tapahtui vasta 15. toukokuuta 1947 Zürichissä. Euler-komissio osallistui onnistuneesti Opera Omnia -lehden julkaisemiseen .
Neljään riviin suunnitellusta 81 volyymista 76 on nyt ilmestynyt (vuodesta 2018 lähtien). Sarjat I (matematiikka: 29 osaa) ja III sarja (fysiikka, varia: 12 osaa) ovat täydellisiä, II sarjan 31 osasta (mekaniikka, tähtitiede) kaksi on edelleen maksamatta (II / 26 ja II / 27 taivaanmekaniikasta) , jonka sisällön pitäisi valmistua aikaisintaan vuoden 2019 aikana. Sarjassa IVA (kirjeenvaihto) on toistaiseksi julkaistu 8 suunnitellusta yhdeksästä niteestä, mukaan lukien kaksi kaksoisosaa IVA / 3 ja IVA / 4. Viimeisimmän osan IVA / 8 vernissage oli 23. marraskuuta 2018. Viimeistä osaa IVA / 9 muokkaa historioitsijaryhmä Antonio Moretton johdolla.
Muita julkaisuja vuosina 1950–1980 Neuvostoliitossa
Kun Eulerin kartano palasi Venäjälle Leningradin akatemian arkistossa, Neuvostoliiton tutkijoille annettiin uusia mahdollisuuksia laajaan tutkimukseen ja he käyttivät tätä tilaisuutta voimakkaasti. Vuonna 1958 Gleb K.Michailow (s. 1929) ja Vladimir Ivanovich Smirnov (1887–1974) raportoivat ensimmäistä kertaa näistä toiminnoista. Lisäksi vuosina 1962 ja 1965 julkaistiin erittäin yksityiskohtainen, mutta kommentoimaton luettelo akatemian arkistoihin tallennetusta Euler-aineistosta kahdessa osassa. Ensimmäisessä osassa on luettelo 2268 kirjeestä Eulerille ja Eulerille (ilman merkintöjä), joita pidetään Pietarin arkistossa. 1950-luvulta lähtien Neuvostoliiton akatemia ja nyt myös Venäjän tiedeakatemia kiinnittivät erityistä huomiota Leonhard Eulerin kirjeenvaihdon indeksointiin ja käsittelyyn, mikä ei sisältynyt Opera omnia Eulerin alkuperäisiin suunnitelmiin . Yhteistyössä Berliinin Saksan tiedeakatemian kanssa yleinen kirjeenvaihto julkaistiin kolmessa osassa ja Eulerin ja Christian Goldbachin kirjeenvaihto. Vuonna 1963 julkaistiin tietyillä tieteellisillä kirjeillä osa, jonka Euler kirjoitti 19 (nuorelle) tutkijalle (kaikki kirjeet käännettiin venäjäksi). Adolf Pavlovič Jušskevič (1906–1993) ja Vladimir Ivanovič Smirnov julkaisivat luettelon Eulerin kirjeistä venäjäksi, joka sisälsi kaikki tunnetut kirjeet Venäjällä ja Venäjän ulkopuolella. Luettelossa on yhteensä 2 654 kirjettä Euleriltä ja Eulerille sekä lyhyt yhteenveto.
1970-luvulla Zürichin Euler-komission ja Neuvostoliiton akatemian välistä yhteistyötä tehostettiin laajentamalla Euler-painosta. Kirjeenvaihto ja tieteelliset muistiinpanot kerätään uuteen Opera omnia Euleri -sarjaan . Tämän sarjan ensimmäinen osa ilmestyi vuonna 1975 ja sisälsi tarkistetun luettelon 2892 kirjeestä kirjeenvaihdosta.
Digitaalisella aikakaudella
Suuri joukko Euler ensisijainen lähteitä ovat vapaasti käytettävissä on Internetissä seurauksena digitoinnin . Sitä vastoin Eulerin Opera omnia ei ole vapaata käyttöä varten, mutta yli 95 prosentin julkaistujen teosten alkuperäisversioiden digitaalikuvat, jotka skannattiin 1700-luvun alkuperäisiltä sivuilta, voidaan kutsua ns. Euleriin arkisto . Entisten opiskelijoiden Lee Stemkosken ja Dominic Klyven katsotaan olevan tämän verkkosivuston perustajia . Verkkoasiakirjoista puuttuu Opera omnia -toimittajien korjaukset ja esittelyt , mutta ne ovat kaikkien ulottuvilla, joilla on Internet-yhteys, ja Euler-arkiston toimittajat lisäävät vähitellen linkkejä kommentteihin ja käännöksiin. Arvioiden mukaan vuoteen 2033 mennessä (Eulerin 250. kuolemavuosi) painettujen ja digitaalisten painosten suhteelliset roolit arvioidaan paremmin.
vastaanotto
Hänen matemaattinen työ inspiroi monia matemaatikkosukupolvia. Hän vaikutti muun muassa Pierre-Simon Laplace , Joseph-Louis Lagrange , Carl Friedrich Gauß , Carl Gustav Jacobi , Niels Henrik Abel , Évariste Galois , Karl Weierstraß ja Bernhard Riemann .
Matemaattiset historioitsijat korostavat Eulerin työn merkitystä nykypäivään asti. Dirk Struik näkee Eulerin ”Hedelmällisyyden” ”yllätyksen ja ihailun lähteenä”. Mitä Eulerin työhön tulee, hän toteaa matemaattisen historian pääpiirteissään vuonna 1967, että sen opiskelu "ei olisi niin vaikeaa kuin miltä näyttää", koska Eulerin latinankielinen kieli on "hyvin yksinkertainen" ja sen termit "melkein muistuttavat nykypäivää". Eulerin menetelmä koostui siirtymisestä yksinkertaisimmista esimerkeistä yleisempään kontekstiin, jolloin esitys oli ristiriidassa nykyään käytetyn abstraktin tyylin kanssa; vastaavasti kritisoitiin myös matemaattisen tarkkuuden puutteita.
Fontit
Leonhard Euleria pidetään yhtenä historian tuottavimmista matemaatikoista. Hänen toistaiseksi keräämät Opera omnia -teokset käsittävät 76 teosta. Hänen julkaisujaan on yhteensä 866. Hänen kootut teokset käsittävät täten arviolta kolmannes koko corpus matemaattisia, fysikaalisia ja mekaanisia tutkimus kolmen viimeisen neljänneksen 18. vuosisadan.
Julkaisut (valinta)
- Mechanica sive motus scientia analytice exposita. 2 osaa, 1736 ( E015 , E016 ).
- Tentamen novae theoriae musicae . 1739 ( E033 ).
- Johdatus aritmeettiseen taiteeseen Pietarin keisarillisen tiedeakatemian kuntosalin käyttöön. 2 nidettä, Academische Buchdruckerey, Pietari; Osa 1 1738, osa 2 1740. ( Digitoitu versio ja kokoteksti saksankielisessä tekstiarkistossa , osa 1, digitoitu versio ja kokoteksti saksankielisessä tekstiarkistossa , osa 2).
- Solutio problematis ad geometriam situs pertinentis. 1741 ( E053 ).
- Methodus inveniendi lineas curves maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti. 1744 ( E065 ).
- Introductio in analysin infinitorum. 2 osaa, 1748 ( E101 , E102 ).
- Découverte d'un nouveau principe de Mécanique. Julkaisussa: Mémoires de l'académie des sciences de Berlin. Osa 6, 1752, s. 185-217 ( E177 ).
- Institutiones calculi differentialis. 2 osaa, 1755 ( E212 ).
- Theoria motus corporum solidorum seu rigidorum. 1765 ( E289 ).
- Kirjeet à une princesse d'Allemagne. 3 osaa, 1768 ( E343 , E344 , E417 ).
- Institutiones calculi integralis. 3 osaa, 1768-1770 ( E342 , E366 , E385 ).
- Täydellinen algebran opas. 2 volyymit, 1770 ( E387 , E388 , volume 2 digitoitu ja koko teksti on saksankielinen teksti arkisto ).
Saksankieliset käännökset ja teosten painokset
- Leonhard Eulerin täydellinen opas integraalilaskennasta. Toimitus Joseph Solomon, 3 osaa, Wien 1828-1830, osa 1, ETH-kirjasto , osa 1, arkistot , osa 2, arkistot , osa 3, arkistot.
- Leonhard Eulerin mekaniikka tai tieteen analyyttinen esitys. 3 osaa, Toimittaja J. Ph. Wolfers, Greifswald 1848-1853, Osa 1, Arkistot , Osa 2, Arkistot , Osa 3, Arkistot.
- Euler, Johann Bernoulli, Jacob Bernoulli: Tutkimus muunnelmalaskelmasta. 1. osa, Ostwalds Klassiker 46, Leipzig 1894, arkisto.
- Euler: Kaksi tutkielmaa pallomaisesta trigonometriasta. Ostwaldin klassikko 73, Leipzig 1896, arkisto.
- Euler: Kolme tutkielmaa karttaprojektiosta. Ostwalds Klassiker 93, Leipzig 1898, arkisto.
- Jakob Bernoulli, Leonhard Euler: Käsittelee tasaisten elastisten käyrien tasapainoa ja värähtelyjä. Ostwaldin klassikko 175, Leipzig 1910.
- Euler: Täydellisempi teoria koneista, jotka käynnistetään veden reaktiolla (1754). Ostwaldin klassikko 182, Leipzig 1911.
- Euler: Kolme tutkielmaa yhtälöiden ratkaisemisesta (1783, 1764, 1790). Ostwaldin klassikko 226, Leipzig 1928.
- Euler: Johdatus äärettömän analyysiin. Osa 1, Wolfgang Walterin johdanto, Springer, 1983.
- Euler: Monimutkaisten toimintojen teoriasta. Johdanto AP Juschkewitsch, Ostwalds Klassiker 261, Akademische Verlagsgesellschaft, 1983.
Opera Omnia
Euler julkaisi noin kaksi tusinaa kirjaa ja 500 tieteellistä artikkelia. Saksalainen matemaatikko Ferdinand Rudio (1856–1929) aloitti kaikkien Eulerin teosten julkaisemisen. Yli 30 nidettä julkaistiin Rudion elinaikanaan. Vuoteen 2013 mennessä oli julkaistu yli 70 yksittäistä nidettä sekä neljä nidettä laajasta kirjeenvaihdosta. Teokset ilmestyvät alkuperäiskielellä, enimmäkseen ranskaksi tai latinaksi.
Kerättyjä teoksia on Birkhäuser (Springer) Verlag julkaissut nimellä Opera Omnia vuodesta 1911 lähtien Ferdinand Rudion perustaman Euler-komission toimesta. Tuolloin julkaisuun osallistuivat myös Adolf Krazer , Rudolf Fueter , Heinrich Weber , Paul Stäckel ja Karl von der Mühll . Myöhempien yksittäisten volyymien toimittajien joukossa olivat Ludwig Schlesinger , Friedrich Engel , Andreas Speiser , Clifford Truesdell (fysiikka, mekaniikka, koko osa 11-1 on joustoteorian historia 1600- ja 1700-luvuilla, kirjoittanut Truesdell), Alexander Mikhailovich Lyapunow , Georg Faber , August Gutzmer , Carl Boehm , Constantin Carathéodory , Henri Dulac , Max Herzberger , Emile Cherbuliez , Charles Blanc ja Eric Aiton (fysiikka). Rudion jälkeen päätoimittajat olivat Andreas Speiser (vuodesta 1928), Walter Habicht (vuodesta 1965) ja vuodesta 1985 lähtien Hans-Christoph Im Hof . Muita toimittajia olivat Emil Fellmann , Adolf Juschkewitsch , Henri Dulac, Pierre Costabel , René Taton , Wladimir Iwanowitsch Smirnow , Alot T. Grigorjan, Joachim Otto Fleckenstein , Johann Jakob Burckhardt , Gleb K. Mikhailov, Franz Lemmermeyer , Andreas Kleinert .
Painos koostuu
- Rivi 1: Matematiikka, 30 osaa (täydellinen). Ensimmäinen osa vuonna 1911 oli algebran käsikirja. Nide 16 koostuu kahdesta osavolyymistä.
- Sarja 2: Mekaniikka ja tähtitiede, 27 osaa 30 ositilassa (täydellinen).
- Rivi 3: Fysiikka ja muut, 12 osaa (täydellinen).
- Rivi 4a: Kirjeenvaihto. Suunniteltu: 9 nidettä noin 3100 kirjeelle, noin 300 kirjeenvaihtajaa. Tähän mennessä julkaistu: 8 osaa.
- Rivi 4b: muistikirjat, päiväkirjat ja julkaisemattomat tuotteet (suunniteltu).
Kirjaimet
Kirjeitä vaihdettaessa Opera Omnian yhteydessä ilmeni seuraavaa :
- Osa 1 (yhteenveto sisällöstä, yleiskatsaus, 1975),
- Osa 2 (Johann I. ja Nikolaus I. Bernoulli),
- Osa 5 ( Clairautin , d'Alembertin ja Lagrangen kanssa ) ja
- Osa 6 (Maupertuisin ja Friedrich II: n kanssa).
Lisäksi seuraava kirjeenvaihto on ilmestynyt Opera Omnian ulkopuolella :
- yhdessä Goldbachin kanssa (Akademie Verlag, Berliini 1965),
- Berliinin ja Pietarin akatemioiden kanssa (Akademie Verlag, Berliini, 3 osaa: 1959, 1961, 1976),
- jossa Tobias Mayer (American Elsevier, 1971).
Vuonna 1845 Paul-Heinrich Fuss julkaisi osia Eulerin kirjeenvaihdosta Goldbachin, Nikolaus Fussin , Johann I: n, Nikolausin ja Daniel Bernoullin kanssa. Lagrangen teoksen painos 14 sisältää myös kirjeenvaihdon Eulerin kanssa.
Yksittäiset todisteet
- ^ William Dunham: Euler: Kaikkien mestari. Mathematical Association of America, 1999, ISBN 978-0-88385-328-3 . S. 17.
- He H. Heuser: Analyysioppikirja II, s. 686.
- ^ Carl B. Boyer, Uta C. Merzbach: Matematiikan historia. John Wiley & Sons, 1991, ISBN 978-0-471-54397-8 . Sivut 439-445.
- ^ Rüdiger Thiele: Leonhard Euler. Leipzig 1982, s. 115.
- ^ Jones, William: Synopsis Palmariorum Matheseos. 243, käytetty 24. helmikuuta 2020.
- ^ Thomas Sonar: 3000 vuotta analyysia. Springer, sivut 455-456.
- ^ Thomas Sonar: 3000 vuotta analyysia. Springer, s.462.
- ^ Thomas Sonar: 3000 vuotta analyysia. Springer, s.463.
- ^ Isaac Newton: Analyysi yhtälöiden numero terminorum infinitas mukaan. 31. heinäkuuta 1669, kirjoitettu latinaksi, osassa De serie progressionum continuanda.
- ^ Raymond Ayoub: Euler ja zeta-toiminto . Julkaisussa: Amer. Matematiikka, kuukausittain . 81, 1974, sivut 1067-86. doi : 10.2307 / 2319041 . S. 1079.
- ↑ Leonhard Euler: Demonstration de la somme de cette suite jne. Alun perin julkaistu Journissa. lit. d'Allemange, de Suisse et du Nord, 2: 1, 1743, s. 115–127.
- ↑ David Harvey: Multimodulaarinen algoritmi lasketuille Bernoulli-numeroille. Lokakuu 2008, (arXiv) .
- ↑ a b Lokenath Debnath: Leonhard Eulerin perintö. Kolmekymmenen vuoden kunnianosoitus. S. 202.
- ↑ Steven R. Finch: Matemaattiset vakiot. Matematiikan ja sen sovellusten tietosanakirja 94, Cambridge University Bridge, 2003, s. 20 ja s.44.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 223.
- ^ Thomas Sonar: 3000 vuotta analyysia. S. 465.
- ↑ Aleksander O. Gelfond: Tietoja L. Eulerin ideoiden matemaattisen analyysin ominaispiirteistä ja johdatus äärettömyyden analyysiin. Julkaisussa: Leonhard Euler 1707 - 1783: Elämä ja työ. S. 106.
- ^ Leonhard Euler: Kirjeenvaihto. Opera omnia, Sarja Quarta A, 1. osa, s.142.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämä ja työ. Sivut 46-47.
- ^ Carl B. Boyer, Uta C. Merzbach: Matematiikan historia. John Wiley & Sons, 1991, ISBN 978-0-471-54397-8 , s. 439-45.
- ^ Emil A.Fellmann: Leonhard Euler 1707 - 1783: Osuudet elämään ja työhön. S.51.
- ^ Emil A.Fellmann: Leonhard Euler 1707 - 1783: Osuudet elämään ja työhön. S.52.
- ^ Thomas Sonar: 3000 vuotta analyysia. S. 456.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä julkaisussa: Leonhard Euler 1707 - 1783: Elämän ja työn vaikutukset. S.47.
- ↑ L.Euler : Institutiones Calculi Integralis , Volume Secundum (1769), toim. F. Engel ja L. Schlesinger, Opera Omnia, ser. 1, voi. 12, Teubner, Leipzig ja Berliini, 1914, s. 242-243
- ↑ P.-S. Laplace: Des Fonctions génératrices , Théorie analytique des Probabilités , (2. painos), Pariisi, 1814, luku I. Osastot 2–20.
- ^ Teun Koetsier: Lakatosin matematiikan filosofia: historiallinen lähestymistapa. North-Holland, 1991, s. 206-210.
- ^ Gerhard Wanner, Ernst Hairer: Analyysi historiansa mukaan. Springer, 2005, s.63.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 216.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. Sivut 235-236.
- ^ Leonhard Euler: Kirjeenvaihto. Opera omnia, Sarja Quarta A, 1. osa, s.134.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 236.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 240.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 242.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 184.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. Sivut 188-189.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämän ja työn vaikutukset , s.36
- ^ William Dunham: Euler. Meidän kaikkien mestari. Osa 22, s. 4-5.
- ^ Chris Caldwell: Suurin tunnettu pääministeri vuodessa. Haettu 26. tammikuuta 2020.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 62.
- ^ Jeff Suzuki: Euler ja lukuteoria: Tutkimus matemaattisessa keksinnössä. Teoksessa: Leonhard Euler: Elämä, työ ja perintö. Sivut 371-372.
- ^ John Stillwell: Matematiikka ja sen historia. 3. painos, Springer, s.423.
- ^ Jeff Suzuki: Euler ja lukuteoria: Tutkimus matemaattisessa keksinnössä. Julkaisussa: Leonhard Euler: Elämä, työ ja perintö , s.375.
- ↑ Herbert Pieper: 1800-luvun Euler: CG Jacob Jacobi. Elem. Math. 60 (2005), 89-107, s. 104.
- ^ Jeff Suzuki: Euler ja lukuteoria: Tutkimus matemaattisessa keksinnössä. Julkaisussa: Leonhard Euler: Elämä, työ ja perintö , s. 381–382.
- ^ Gary Cornell, Joseph H.Silverman, Glenn Stevens: modulaariset muodot ja Fermatin viimeinen lause , Springer, s.10
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 98.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. Sivut 343-344.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 71.
- ^ Wright Hardy: Johdanto numeroteoriaan. Clarendon Press 1975, s.286.
- ^ William Dunham: Euler: Kaikkien mestari. Mathematical Association of America, 1999, ISBN 978-0-88385-328-3 . Luvut 3 ja 4.
- ↑ a b Lokenath Debnath: Leonhard Eulerin perintö. Kolmekymmenen vuoden kunnianosoitus. S. 80.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 81.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämän ja työn vaikutukset , s.93.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. P. Xvii.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 178.
- ↑ Steven R. Finch: Matemaattiset vakiot. Matematiikan ja sen sovellusten tietosanakirja 94, Cambridge University Bridge, 2003, s.30.
- ↑ Ronald S.Calinger: Leonhard Euler: Matemaattinen nero valaistumisessa. Princeton University Press, 2016, s.107.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämän ja työn vaikutukset , s. 52–53.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 137.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämän ja työn vaikutukset , s. 53–54.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämä ja työ. S.56.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämä ja työ. S. 58.
- B a b c David Richeson: Polyhedraalikaava. Teoksessa: Leonhard Euler: Elämä, työ ja perintö. S. 421.
- ↑ David Richeson: polyhedraalisen Formula. Teoksessa: Leonhard Euler: Elämä, työ ja perintö. S. 425.
- ^ Alan Gibbons: Algoritminen graafiteoria. Cambridge University Press, 1985, s. 72, ISBN 978-0-521-28881-1 .
- ↑ David Richeson: polyhedraalisen Formula. Julkaisussa: Leonhard Euler: Elämä, työ ja perintö , s.428.
- ^ AL Cauchy (1813). Tutkimus les polyèdresistä - pääministeri. Journal de l'École Polytechnique. 9 (Cahier 16): sivut 66-86.
- ↑ S.-A.-J. L'Huillier (1861): Mémoire sur la polyèdrométrie. Annales de Mathématiques. 3: 169 - 89.
- ↑ Andreas Verdun: Leonhard Eulerin työ taivaanmekaniikasta. Springer, s.10.
- ↑ David Richeson: polyhedraalisen Formula. Julkaisussa: Leonhard Euler: Elämä, työ ja perintö , s. 436–437.
- ↑ Gerald Alexanderson: Eulerin ja Königsbergin sillat: historiallinen näkymä. American Mathematical Societyn tiedote. 43 (4), heinäkuu 2006: 567-573, doi: 10.1090 / S0273-0979-06-01130-X . S. 567.
- ^ Leonhard Euler: Commentarii academiae scientiarum imperialis Petropolitanae. Euler-arkisto.
- ^ Leonhard Euler: Solutio problematis ad geometriam situs pertinentis . Commentarii academiae scientiarum imperialis Petropolitanae (CASP), osa 8.
- ↑ Gerald Alexanderson: Eulerin ja Königsbergin sillat: historiallinen näkymä. American Mathematical Societyn tiedote. 43 (4), heinäkuu 2006: 567-573, doi: 10.1090 / S0273-0979-06-01130-X . S. 567.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. P. Xiv.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 217.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 273.
- ↑ Hui Cheng, KC Gupta: historiallinen huomautus lopullisista kierroksista. Julkaisussa: Journal of Applied Mechanics. Osa 56, nro 1, maaliskuu 1989, s. 139-145, doi: 10.1115 / 1.3176034 .
- ^ Leonhard Euler: Formulas generales pro translatione quacunque corporum rigidorum. Julkaisussa: Novi Commentarii academiae scientiarum Petropolitanae. Osa 20 (1775), 1776, s. 189-207.
- ↑ Lokenath Debnath: Leonhard Eulerin perintö, A Tribute Tricentennial , s. 328-329
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 341.
- ^ RE Bradley: Eulerin analyysi Genovan arpajaisista. 2004.
- ^ Leonhard Euler: Réflections sur une espèce singulière de loterie, nommée Loterie génoise. (E 812).
- ^ DR Bellhouse: Euler ja arpajaiset. Teoksessa: Leonhard Euler: Elämä, työ ja perintö. Sivut 387-388.
- ^ AJ Lotka: Tutkimukset materiaaliaineiden kasvumoodista. American Journal of Science, 24, 199-216.
- ^ Enric Cortés: Näkymät väestönkasvun sisäiselle nopeudelle. Methods in Ecology and Evolution, 7 , 2016, 1136-1145, s.1136.
- ↑ John Van Sickle, CAM Attwell ja G.Colin Craig: Väestönkasvun arvioiminen luonnollisten kuolemien ikäjakaumasta. Journal of Wildlife Management, osa 51, nro 4 (lokakuu 1987), s. 941-948.
- ↑ Andreas Verdun: Leonhard Eulerin työ taivaanmekaniikasta. Springer, s.10.
- ^ SG Langton: Euler jäykistä rungoista. Teoksessa: Leonhard Euler: Elämä, työ ja perintö. S. 195.
- ↑ a b c Andreas Verdun: Leonhard Eulerin työ taivaanmekaniikasta. Springer, s.11.
- ^ Thomas Sonar : 3000 vuotta analyysia. Springer, sivut 454-455.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. Sivut 297-298.
- Bal F. Balck: Eulerin essee reaktioturbiinin fysiikasta - tärkeä osa vesipyörien, turbiinien ja muiden energianmuunnoslaitteiden teknistä historiaa. Sivut 378-405.
- ↑ Andreas Verdun: Leonhard Eulerin työ taivaanmekaniikasta. Springer, s.13.
- ↑ Andreas Verdun: Leonhard Eulerin työ taivaanmekaniikasta. Springer, s.283.
- ↑ Ronald S.Calinger: Leonhard Euler: Matemaattinen nero valaistumisessa. Princeton University Press, 2016. ISBN 978-1-4008-6663-2 , s.384.
- ^ VJ Katz: Trigonometristen toimintojen laskenta. Historia Mathematica, 14: 311 - 324 (1987).
- ^ C. Wilson: Analyyttisen matematiikan Euler ja sovellukset tähtitieteeseen. Julkaisussa: Leonhard Euler: Elämä, työ ja perintö , s.123.
- ^ Newton: Principia. Kirja III, ehdotus 13.
- ^ Leonhard Euler: Recherches sur le movement des corps céléstes en générale. Mémoires de l'Académie des Sciences de Berlin 3 (1747), 93-143; Leonhard Euler: Oopperan omnia. Ser. 2, 25, s. 1-44.
- ^ Leonhard Euler: Recherches sur la question des inégalités du muou de de Saturne et de Jupiter. Aihe ehdottaa vuodelta 1748, nimeltään Académie Royale des Sciences.
- ^ C. Wilson: Analyyttisen matematiikan Euler ja sovellukset tähtitieteeseen. Teoksessa: Leonhard Euler: Elämä, työ ja perintö , s. 125–126.
- ^ Christa Jungnickel, Russell McCormmach: Cavendish - kokeellinen elämä. S. 155.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämä ja työ. S. 67.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 361.
- ↑ David Speiser: Eulerin kirjoitukset optiikasta, sähköstä ja magnetismista. Julkaisussa: Leonhard Euler 1707–1783: Elämän ja työn vaikutukset. S. 218.
- ↑ Benjamin Robins, Leonhard Euler: Tykistön uudet periaatteet, jotka sisältävät jauheen voiman määrittämisen sekä tutkimuksen ilman nopeiden ja hitaiden liikkeiden vastuksen eroista. Verkossa osoitteessa: echo.mpiwg-berlin.mpg.de. (European Cultural Heritage Online), käyty 24. joulukuuta 2016.
- ↑ Leonhard Euler: Johdatus äärettömän analyysiin: Osa 1. Springer Verlag Berlin Heidelberg GmbH, s. 11 (johdanto uusintapainokseen).
- ↑ Bouger, Euler: Aluksen hydrostaattisen vakauden teorian perustaksi. Julkaisussa: Shipbuilding Society Yearbook. Vuosikerta 98, 2004, s.183.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämän ja työn vaikutukset , s.26.
- ^ O. Neumann: Syklotomia : Euleristä Vandermonden kautta Gaussiin. Julkaisussa: Leonhard Euler: Elämä, työ ja perintö , s. 324 ja sitä seuraavat.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 88.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämän ja työn vaikutukset , s.40.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. 95.
- ↑ Ronald S.Calinger: Leonhard Euler: Matemaattinen nero valaistumisessa. Princeton University Press, 2016, s.467.
- Ina Nina I. Nevskaja: Leonhard Euler ja tähtitiede. Julkaisussa: Leonhard Euler 1707 - 1783: Elämän ja työn vaikutukset , s. 367–368.
- ^ Leonhard Euler: Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae. Pietari 1739.
- ^ Peter Pesic: Musiikki ja modernin tieteen tekeminen. S. 133.
- ↑ Martin Vogel: Oppi äänisuhteista; Kustannustalo systemaattisen musiikkitieteen GmbH: lle, Bonn - Bad Godesberg 1975, Orpheus-julkaisusarja, nide 16, ISBN 978-3922626091 ; S. 136
- ↑ Tässä tarkoitetaan kahden tai useamman samanaikaisesti soivan äänen taajuussuhteita.
- ↑ Vogel, Tonbeektiven, s.146
- ↑ Daniel Muzzulini: Leonhard Eulerin konsonanssi. Musiikkiteoria, 9 (2), s.2.
- ↑ Daniel Muzzulini: Leonhard Eulerin konsonanssi. Musiikkiteoria, 9 (2), s.6.
- ^ Peter Pesic: Eulerin musiikimatematiikka . Springer Science + Business Media New York, osa 35, numero 2, 2013, s.38.
-
^ Mark Lindley ja Ronald Turner-Smith: Musikaalivaakojen matemaattiset mallit. Bonn, Systemaattisen musiikkitieteiden kustantamo, 1993, s. 234–39.
Katso myös Catherine Nolan: Musiikkiteoria ja matematiikka. Cambridge History of Western Music Theory, Th. Christensen toim., New York, CUP, 2002, s.278-79. - ↑ Patrice Bailhache: La Musique traduite en Mathématiques: Leonhard Euler. Haettu 8. helmikuuta 2020.
- ↑ Jos esimerkiksi lisäät alkuluvun 7 alkulukujen 3 ja 5 lisäksi, pääset viidenteen, kolmanteen ja seitsemänteen järjestelmään. Tässä järjestelmässä saadaan esimerkiksi B. erityisen yksinkertaiset taajuussuhteet hallitsevassa seitsemännessä soinnussa, nimittäin 4: 5: 6: 7.
- ↑ Vogel, Tonbeektiven, s. 139f
- ↑ Vogel, Tonbeektiven, s.143
- ↑ Vogel, Tonbeektiven, s. 144ff
- ↑ Vogel, Tonbeektiven, s.145f
- ↑ Vogel, Tonbeektiven, s.148
- ↑ Vogel antaa esimerkin tällaisesta kritiikistä: J.Jeans, Science and Music, Cambridge 1961, 155
- ↑ Vogel, Tonbeektiven, s.147 viittaamalla L.Euleriin, Opera omnia, III 1, 512
- ↑ Vogel, Tonbeektiven, s.149 viittaamalla L.Euleriin, Opera omnia, III 1, 521
- ↑ Mikä on Euler Fokker-suku? Haettu 27. helmikuuta 2020.
- Ric Eric Emery: Temps et musique. Lausanne, L'Âge d'homme, 2000, s. 344–45.
- Matth Johannes Mattheson: Suuri yleinen bassoopisto . Hamburg, 1731, osa I, s. 104-06, mainitsi Euler; ja näyte urkuriharjoituksesta. Hampuri, 1719, sivut 57-59.
- ^ Wilfrid Perret: Joitakin musiikkiteorian kysymyksiä. Cambridge, 1926, sivut 60-62; Mikä on Euler-Fokker-suku? Haettu 8. helmikuuta 2020.
- ^ Leonhard Euler: Tentamen novae theoriae musicae. Pietari, 1739, s. 147; De harmoniae veris principiis. Pietari, 1774, s.350.
- ^ Edward Gollin: Eulerin Speculum Musicumin yhdistelmä- ja muutosnäkökohdat. Matematiikka ja laskenta musiikissa, T. Klouche ja Th. Noll toim., Springer, 2009, s. 406-11.
- ↑ Kirjeitä luonnonfilosofian eri aiheista. S.2.
- ^ Leonhard Euler: Lettres de M.Euler à une princesse d'Allemagne. Lettre I, s.3.
- ^ Leonhard Euler: Lettres de M.Euler à une princesse d'Allemagne. Lettre XVI, s.63.
- ^ Lettres de M.Euler à une princesse d'Allemagne sur différentes kysymyksiä de fysiikka ja filosofia. Nouvelle Edition, Avec des Additions, par MM. Le Marquis de Condorcet et De La Croix, Pariisi, 1787.
- ↑ Ronald S Calinger, Ekaterina (Katya) Denisova, Elena N Polyakhova: Leonhard Eulerin kirjeet saksalaiselle prinsessalle. IOP Concise Physics, Morgan and Claypool Publishers, 2019, s.2--13.
- ^ AP Juskevic, E. Winter: Leonhard Euler ja Christian Goldbach: Kirjeenvaihto. 1729–1764, Akademie-Verlag, Berliini, 1965.
- ↑ Leonhard Euler: Solution d'une-kysymyksen curieuse que ne paroit soumise à aucune -analyysi. 1766.
- ↑ a b Lokenath Debnath: Leonhard Eulerin perintö. Kolmekymmenen vuoden kunnianosoitus. S. 162.
- ↑ D. Klyve ja L. Stemkoski: Graeco-Latin-neliöt ja Eulerin virheellinen arvelu . College Mathematics Journal, osa 37, nro. 1 (tammikuu 2006), 2-15, s.13.
- ^ Robert E. Bradley, C. Edward Sandifer (toim.): Leonhard Euler: Elämä, työ ja perintö. Elsevier, 2007, s.443.
- ^ P. Stäckel, W. Ahrens: Kirjeenvaihto CG Jacobin ja PH v. Jalka Leonhard Eulerin teosten julkaisemiseen. Journal for the History of Mathematical Sciences, Leipzig, 1907–1908, s. 235 f.
- ↑ oeuvres täydentää de L. Euler. , 5 osaa, Bryssel, 1838–1839.
- ^ Henri Bosmans: Sur une preliminative d'édition des œuvres complètes de L. Euler faite à Bruxelles en 1839. Louvain 1909.
- ↑ Andreas Kleinert: Leonhardifahrt Euleri Opera Omnia: satavuotisjuhla. EMS Newsletter syyskuu 2007, s.26.
- ↑ Andreas Kleinert: Leonhardifahrt Euleri Opera Omnia: satavuotisjuhla. EMS Newsletter syyskuu 2007, s.26.
- ^ Emil A.Fellmann: Leonhard Euler: Essee elämästä ja työstä. Julkaisussa: Leonhard Euler 1707 - 1783: Elämän ja työn vaikutukset , s.52.
- ^ F. Rudio, K. Schröter: Huomautuksia Sveitsin kulttuurihistoriasta: 21. Leonhard Eulerin syntymäpäivän kaksikymmenvuosi; 22. Suunnitelma Eulerin teosten täydellisestä painoksesta. Julkaisussa: Natural Research Society, Quarterly julkaisu Zürichissä 52 (1907), s. 537–546, tässä: s. 541.
- ↑ Ch. Gehring-Straube: Epätoivotut ajat. Sveitsin ja Neuvostoliiton suhde katkeamisen ja suhteiden jatkamisen välillä (1918–1946) perustuu sveitsiläisiin tiedostoihin. Zürich 1997.
- ↑ A.Kleinert: Sata vuotta Venäjän ja Sveitsin yhteistyötä EULER-kokonaispainoksessa. Euroopan tiedesuhteet toim. Dietrich von Engelhardt, Ingrid Kästner, Jürgen Kiefer, Karin Reich (nide 14), s. 213–222.
- ↑ Katso Opera Omnia Leonhard Euler. Julkaisussa: Luonnontieteet Sveitsi. Haettu 12. huhtikuuta 2020.
- ^ GI Michajlov ja VI Smirnov: Neopublikovannye materialy Leonarda Ėjlera v Arkisto Akademii nauk SSSR. (Julkaisematon Eulerin aineisto Neuvostoliiton tiedeakatemian arkistossa), julkaisussa: Leonard Ėjler. Sbornik statej v cest '250-letija so dnja rozdenija, predstavlennych Akademii nauk SSSR (paperikokoelma Eulerin 250. syntymäpäivän kunniaksi). Moskova: Izdatel'stvo Akademii nauk SSSR, viite. S.47.
- ↑ Rukopisnyemateriaalisesti Leonarda Ėjlerav -arkisto Akademiiu nauk SSSR. (Eulerin käsinkirjoitettu aineisto Neuvostoliiton tiedeakatemian arkistossa), 2 osaa. (Trudy Archiva 17 ja 20). Moskova-Leningrad: Izdatel'stvo Akademii nauk SSSR 1962, Leningrad: Nauka 1965.
- ^ Berliinin ja Pietarin tiedeakatemia Leonhard Eulerin kirjeenvaihdossa. AP Juškevič ja E. Winter, toim., Yhteistyössä P. Hoffmannin, TN Kladon ja Ju. Ch. Kopelevič, 3 osaa (= Lähteet ja tutkimuksia Itä-Euroopan historiasta, III / 1–3). Berliini: Akademie-Verlag 1959, 1961, 1976.
- ^ Leonhard Euler ja Christian Goldbach. Kirjeenvaihto 1829-1764. AP Juškevič ja E. Winter, toim., Yhteistyössä P. Hoffmannin, TN Kladon ja Ju. Ch. Kopelevič (tutkielmat Berliinin Saksan tiedeakatemiasta, filosofian, historian, poliittisten, oikeus- ja taloustieteiden luokka, syntynyt 1965, nro 1). Berliini: Akademie-Verlag 1965.
- ↑ L. Ėjler, Pis'ma k učenym (Kirjeitä tutkijoille). Moskova-Leningrad: Izdatel'stvo Akademii nauk SSSR 1963.
- ↑ L. Ėjler: Perepiska. Annotirovannyj ukazatel (Kirjeenvaihto. Seliteellinen luettelo). Leningrad: Nauka 1967.
- ^ Peter Hoffmann: Leonhard Euler ja Venäjä. Teoksessa: Leonhard Euler: Elämä, työ ja perintö. Sivut 72-73.
- ^ JJ Burkhardt: Sveitsin luonnontieteellisen seuran Euler-toimikunta: Panos julkaisujen historiaan. Julkaisussa: Leonhard Euler 1707-1783. JJ Burckhardt et ai., Toim. Birkhäuser, Basel 1983, s. 501-510.
- ↑ Leonardi Euleri -ooppera omnia, ser. 4. Leonardi Euleri commercialium epsitolicum. Osa A1: Descriptio commercialii epistolici. Birkhäuser, Basel 1975.
- ^ Peter Hoffmann: Leonhard Euler ja Venäjä. Julkaisussa: Leonhard Euler: Elämä, työ ja perintö , s.73.
- ↑ C.Edward Sandifer, Robert E.Bradley: Leonhard Euler: Elämä, työ ja perintö. Sivut 3-4.
- ↑ Herbert Pieper: 1800-luvun Euler: CG Jacob Jacobi. Matematiikan elementit, Swiss Mathematical Society, 2005, s.98.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. S. xix.
- ↑ Dirk Jan Struik: Yhteenveto matematiikan historiasta. Springer, s.139.
- ^ Rüdiger Thiele: Leonhard Euler. Leipzig 1982, s. 158-160.
- ^ Thomas Sonar: 3000 vuotta analyysia. Springer, s.448.
- ↑ Lokenath Debnath: Perintö Leonhard Euler. Kolmekymmenen vuoden kunnianosoitus. P. Vii.
- ↑ Andreas Verdun: Leonhard Eulerin työ taivaanmekaniikasta. Springer, S. XI.
- ↑ Walter Guatschi: Leonhard Euler: Hänen elämänsä, ihminen ja hänen teoksensa . SIAM Review, osa 50, nro 1, s. 3-33, doi: 10.1137 / 070702710 , s.3 .
- ↑ James J.Tattersall: Alkeisnumeroteoria yhdeksässä luvussa. S. 18.
- ^ W. Dunham: Eulerin nero: Heijastuksia hänen elämäänsä ja työhönsä. S. 15.
- ↑ Clifford Truesdell: Joustavien elastisten kappaleiden järkevä mekaniikka 1638–1788. 1960.
- ↑ Hans-Christoph Im Hof, Andreas Kleinert ja muut: Leonhard Euler, Opera omnia. Julkaisussa: Birkhauserin tieteenhistoria. Verkossa: Springer.com. Haettu 24. joulukuuta 2016.
- ^ Andreas Kleinert, Matthias Mattmüller: Leonhardi Euleri Opera Omnia: satavuotisjuhla. EMS Newsletter, syyskuu 2007, ISSN 1027-488X (PDF; 1,88 MB), verkossa osoitteessa: Euler-2007.ch. Haettu 24. joulukuuta 2016.
- ↑ Lagrange, œuvre. Osa 14, Gallica.






































































































































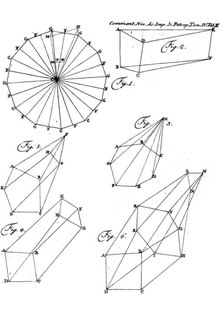
















![{\ displaystyle \ int _ {1} ^ {N} {\ frac {1} {x ^ {2}}} \ mathrm {d} x = \ left [- {\ frac {1} {x}} \ right ] _ {1} ^ {N} = 1 - {\ frac {1} {N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2566a17e1c5d3889f1d3c6bd8fb74822584d5df9)








































![{\ displaystyle {\ sqrt [{12}] {2}} \ noin 1,059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40cdb2ae486a0cf1ea97d61be2fa246dbaa2caa2)